모멘트 규모
| 시리즈의 일부 |
| 지진 |
|---|
모멘트 규모(Moment magnitude scale, 약자 MMS, 기호 )는 지진 모멘트를 이용해 지진의 절대적인 에너지 크기인 지진 규모를 측정하는 척도이다. 1979년 토마스 C. 행크스와 가나모리 히로오가 처음으로 개발하였다. 1935년 찰스 릭터가 개발한 규모 단위인 릭터 규모와 비슷하게 로그 척도를 사용한 단위이다.
모멘트 규모는 지진의 강도 순 크기와 같이 특정한 지진의 규모를 매길 때 가장 많이 사용하는 규모 척도이다.[1] 모멘트 규모는 다른 규모보다 지진이 방출한 에너지와 더 직접적인 관련이 있으며 또한 '포화' 현상도 일어나지 않아 특정 조건에서도 다른 규모 단위처럼 지진의 규모를 과소평가한다는 문제점이 발생하지 않는다.[2] 미국 지질조사국(USGS) 등 여러 지진 관련 기관에서도 통상 규모 M5 이상의 큰 지진을 릭터 규모나 표면파 규모(Ms) 대신 모멘트 규모를 기준으로 발표한다.[3] 모멘트 규모의 하위 단위인 Mww와 같은 여러 단위들은 모멘트 규모 계산에 필요한 지진 모멘트를 어떻게 계산하는지에 따라서 달라진다.
역사[편집]
릭터 규모: 최초의 지진 규모[편집]

20세기 초만 하더라도 지진이 어떻게 일어나는지, 지진파가 지각에서 어떻게 생성되고 전파되는지, 지진이 일어나는 도중 지각이 파열되는 과정은 어떻게 진행되는지 거의 알려지지 않았다. 따라서 최초로 만들어진 규모 척도는 경험적인 분류 체계였다.[4] 지진의 규모를 경험적으로 결정한 최초의 시도는 1931년 일본의 지진학자인 와다치 기요가 지진의 지진파의 최대 진폭은 일정한 비율로 진앙과의 거리에 따라 점점 줄어든다는 사실을 발견하고서부터이다.[5] 이후 미국의 지진학자 찰스 릭터는 지진계에 기록된 궤적의 진폭이 로그함수 단위로 차이나도록 진앙과의 중심거리를 조정하는 방법을 발견하였고, 지진을 내부적으로 일관되고 방출한 에너지의 추정치와 대략적으로 맞출 수 있는 일종의 "규모 단위"로 사용할 수 있다는 점을 발견하였다.[6] 릭터는 기준점을 세워 규모가 1 증가할때마다 지진파의 진폭이 10배 단위로 늘어나게 설계한 단위를 1935년 자신의 논문에서 "규모 단위"라는 이름으로 처음으로 공개했는데, 이것이 바로 ML이라는 약자로 부르는 국지 규모 혹은 릭터 규모이다.[7]
국지 규모는 표면파가 크게 관측되는, 진앙과 약 100 - 600 km 떨어진 지점에서 발생한 진원 깊이가 15 km 이하로 매우 얕은 천발지진인 중간 규모의 지진을 측정한다는 전제로 짜여졌다. 깊이가 깊을수록, 진앙 거리가 멀수록, 규모가 클수록 표면파의 규모는 현저하게 줄어들기 때문에 국소 규모는 지진의 규모를 과소평가한다. 이 문제를 해결하기 위해 다른 규모도 개발되기 시작해[8] 1945년에는 베노 구텐베르크가 표면파 규모(MS)를 개발하였고,[9] 1956년에는 구텐베르크와 릭터가 실체파 규모(mB)를 개발하였으며[10] 그 외도 여러 변형형이 개발되어 국소 규모의 문제점을 보완하였지만 그럼에도 전부 포화 문제가 발생하였다. 특히 1970년대 자주 사용했던 표면파 규모가 MS8.0 인근에서 포화되기 시작하기 때문에 1960년 발디비아 지진이나 1964년 알래스카 지진과 같은 초거대지진이 방출하는 에너지를 매우 과소평가한다는 문제점이 있었다.[11] 두 지진의 표면파 규모는 각각 MS8.5, MS8.4로 측정되었지만 그동안 알려졌던 M8 규모의 지진보다 파괴력이 굉장히 강했으며, 실제로 두 지진의 모멘트 규모는 각각 Mw9.6, Mw9.3이었다.[12]
단일결합과 이중결합[편집]

지진에 관한 연구는 근원이 되는 단층파열 사건을 직접 관찰할 수 없고, 지진의 지진파가 근원이 되는 사건에 대해 무엇을 말해줄 수 있는지 설명할 수 있는 수학적 방법을 개발하는데 시간이 많이 소요되었기 때문에 매우 어려웠다. 초기 지진 연구에서는 지진으로 관측하는 지진파와 동일한 파형을 만들어 낼 수 있는 서로 다른 힘을 받는 체계가 무엇이 있는지 연구하는 일이 진행되었다.[13]
가장 간단한 체계는 물체에 하나의 단일한 힘이 작용하는 경우이다. 이 때 저항을 넘을 수 있을 정도로 충분한 힘이 걸리게 되면 물체는 움직이게 된다('변환' 과정). 하지만 같은 '작용선'이지만 서로 반대 방향으로 작용하는 두 힘이 걸리게 되면 두 힘은 서로 상쇄된다. 만약 두 힘이 정확하게 같아 상쇄된다면 순변환은 존재하지 않지만, 그렇지 않다면 장력이나 압축력과 같이 물체는 지속적인 응력을 받을 것이다. 평행하지만 서로 별개의 작용선에서 작용하는 두 힘이 상쇄된다면 물체는 회전력, 토크가 작용한다. 힘의 상호작용에 관한 물리학의 한 분야인 역학에서는 이 모델을 '결합'모델 중 하나로 단일결합(Single Couple)과 이중결합(Double Couple) 모델이라고 부른다. 두 쌍의 힘이 서로 동등하고 규모가 정확히 반대라면 토크는 아에 걸리지 않으며 이를 이중결합이라고 부른다.[14] 이중결합은 "동시에 직각 방향으로 작용하는 압축력과 인장력의 합"이라고 표현할 수 있다.[15]
1923년 일본의 지진학자 나카노 히로시는 특정 지진파형들은 이중결합 모델 관점으로 잘 설명할 수 있다는 점을 보여주었다.[16] 이후 진원을 모델링하는 가장 좋은 방법에 대해 단일결합과 이중결합 두 모델이 30년 넘게 경쟁하며 논쟁을 벌이게 된다.[17] 일본의 지진학계는 이중결합설을 지지했지만, 그 외 대부분의 국가 내 지진학계에서는 단일결합설을 지지하였다.[18] 단일결합 모델에는 몇 가지 단점이 있긴 했지만 일견 간단해 직관적으로 보였고, 지진 발생을 설명하기 위한 탄성발발설이 맞기 위해서는 단일결합모델만 사용할 수 있다는 믿음이 있었다.[19] 원칙적으로 두 모델은 S파의 반사 패턴 차이를 통해 구별할 수 있지만 관측 자료의 품질이 낮아 이를 확인할 수 없었다.[20]
이 논쟁은 1963년 마루야마, 1964년 하스켈, 1964년 버리지와 노포프가 지진이 일어날 때 파열을 단층운동(Dislocation)으로 모델링할 경우 나타나는 지진학적 복사파 패턴이 항상 이중결합 모델로만 설명할 수 있는 패턴과 같으며, 단일결합 모델에서 발생하는 패턴으로는 설명할 수 없다는 것을 증명하면서 끝났다.[21] 이는 세계 표준 지진관측망(WWSSN)을 구축하여 얻은 풍부하고 질높은 데이터를 통해 지진파를 더욱 면밀하게 분석할 수 있게 되면서 가능한 일이었다. 특히 1966년 아키 게이이치는 1964년 발생한 일본 니가타 지진에서 이중결합에 기초해 지진파에서 계산해서 도출한 지진 모멘트가 관측한 물리적인 단층운동에서 계산한 지진 모멘트와 동일하다는 점을 입증하였다.[22]
단층운동 이론[편집]
이중결합 모델은 지진의 원거리 지진파 방출 패턴을 설명할 순 있지만, 지진 원점에서 흔들림이 발생하는 이유나 물리적 특징에 대해서는 설명할 수 있는 것이 거의 없다.[23] 단층을 따라 암반이 미끄러지면서 지진이 발생한다는 단층지진설 이론이 정립되었지만(그 외에는 마그마의 움직임으로 지진이 발생한다는 마그마 관입설이나 상변화에 따른 급격한 부피변화설이 있다[24]) 이를 직접 깊은 곳에서 관찰하는 것은 불가능했고 지진파를 통해 지진의 근원 원리를 연구하기 위해서는 진원 메커니즘을 이해해야 했다.[25]
지진이 지진파를 발생시키는 물리적인 과정을 모델링하기 위해서는 1907년 비토 볼테라가 처음으로 공식화하고 1927년 어거스터스 에드워드 호그 러브가 발전시킨 전위 이론의 발전이 필요했다.[26] 더욱 일반적인 재료과학적 응력 문제에 적용하기 위해[27] 1951년 프랭크 네베로가 이론을 확대하였고 러시아의 지구물리학자 A. V. 베덴스카야가 지구의 단층에도 적용시킬 수 있음을 증명하였다.[28] 1956년 발표된 논문에서 이 연구팀은 지진의 진원 메커니즘의 일부를 결정하기 위해 전위 이론을 사용하였고, 미끄러지면서 발생하는 파열 과정에서 일어나는 재료과학적인 전위가 실제로 이중결합 이론과 같다는 것을 증명하였다.[29]
1958년 발표된 두 논문에서 J. A. 스테케테는 전위 이론을 지구물리학적 특징과 연결시키는데 성공했다.[30] 여러 연구자들이 다른 세부사항을 밝혀냈으며[31] 1964년 버리지와 노포프가 이중결합 이론과 탄성발발설을 확립하고 지진의 물리적 특징을 지진 모멘트와 연관시키는 기초를 제공하며 일반적인 이론 확립에 성공하였다.[32]
지진 모멘트[편집]
지진 모멘트, 약자로 M0은 단층이 미끄러지고 지진이 발생한 면적을 측정한 값이다. 지진 모멘트의 값은 지진의 이중결합 토크와 동등한 두 힘 각각의 토크값을 의미한다.[33] 정확히 말하면 이중결합의 각 성분을 의미하는 2차 모멘트 텐서의 스칼라값이다.[34] 지진 모멘트는 뉴턴 미터(N·m) 혹은 줄 단위로 표기하며, 구 CGS 단위계에서는 다인 센치미터(dyn-cm) 단위로 표기하기도 한다.[35]
지진파를 이용해 지진 모멘트를 최초로 계산한 시점은 1964년 일본에서 니가타 지진이 발생했을 때 아키 게이이치의 계산이었다.[36] 아키 게이이치는 두 가지 방법으로 지진 모멘트를 계산했다. 첫번째로는 세계 표준 지진관측망(WWSSN)의 먼 지진관측소 데이터를 사용하여 장주기 지진파(주기 약 200초, 파장 약 1,000 km)를 분석하여 지진의 등가 이중결합의 크기를 측정하였다.[37] 두번째로는 버리지와 노포프의 전위이론을 연구하여 단층이 미끄러진 폭, 방출한 에너지, 스트레스 강하(기본적으로 방출되는 퍼텐셜 에너지의 양)을 측정하였다.[38] 특히 게이이치는 지진의 지진 모멘트를 물리 매개변수와 연관시키는 유명한 아래 방정식을 개발하였다.
- M0 = μūS
여기서 μ는 표면적 S인 단층이 평균 ū의 거리만큼 전위할 때 강성도(혹은 전위 저항)을 의미한다. 현대에 와서는 ūS를 "기하학적 모멘트" 혹은 "전위도"로 알려진 똑같은 값인 D̄A로 대체한다.[39] 위 방정식에 따르면 지진파에서 계산한 이중결합으로 도출한 지진 모멘트는 단층이 미끄러진 표면적과 미끄러진 양의 정보로 계산된 모멘트와 연관성이 높다는 사실을 알 수 있다. 1964년 니가타 지진의 경우 지진 모멘트를 통해 추정한 전위가 실제로 지질학적 분석을 통해 관측된 전위와 거의 일치하였다.[40]
지진 모멘트는 지각의 비탄성적인(강체 운동) 변위 혹은 왜곡을 일으키는 일, 정확히는 돌림힘의 크기를 가리키는 척도이다.[41] 즉 지진 모멘트는 지진으로 방출한 총 에너지와 큰 관련이 있다. 하지만 지진의 위력이나 잠재적인 파괴력은 (다른 요인들 중에서도) 총 에너지 중 얼마가 지진파로 변환되냐에 따라 달라진다.[42] 일반적인 지진은 총 에너지의 10% 이하가 지진파로 변환되며, 나머지 에너지는 암석을 파쇄하고 단층의 마찰력을 이기는 데 사용되며 열에너지 형태로 방출된다.[43]
그럼에도 지진 모멘트는 지진의 물리적인 크기를 다른 매개변수보다도 더욱 직접적으로 알려주는[44] 지진 규모의 가장 기본적인 척도이다.[45] 1975년 초에는 "가장 신뢰성 높게 결정되는 지진 발생원의 매개변수 중 하나"로 간주되었다.[46]
에너지를 따르는 모멘트 규모의 도입[편집]
대부분의 지진 규모 척도는 진원과 표준적인 거리만큼 떨어진 곳에서 표준 주파수의 지진파 파동의 진폭이 어느정도인지만 측정하고 이를 서로 비교한다는 점 때문에 지진 규모를 지진의 물리적 속성과 서로 연관짓기 매우 어렵다는 문제가 있었다. 구텐베르크와 릭터는 지진의 복사 에너지 Es가 다음 공식으로 추정할 수 있다고 주장했다.
여기서 위 식의 단위는 줄(J)이다. 불행히도 수많은 거대지진의 지진 지속 시간은 표면파 규모 Ms의 측정에 사용되는 표면파 측정 주기인 20초보다 긴 경우가 대부분이었다. 이 때문에 1960년 칠레 발디비아 지진(Mw9.5)와 같은 거대지진의 표면파 규모가 Ms8.2라는 매우 낮은 값으로 측정되었다. 칼텍의 지진학과 교수인 가나모리 히로오는 이 문제를 인식하고 복사 에너지의 추정치를 통해 역으로 규모를 정의하는 간단하지만 중요한 단계를 밟았으며 이를 통해 정의한 규모 Mw(w는 '일' 혹은 에너지를 뜻하는 work의 두문자어)의 식은 아래와 같다.[47]
가나모리는 복사 에너지를 측정하는 행위가 전체 주파수 대역에서 파동 에너지를 하나로 합쳐야 하기 때문에 기술적으로 매우 어려움을 인식하였다. 계산을 단순화하기 위해 가나모리는 여러 스펙트럼에서 가장 낮은 주파수 영역으로 스펙트럼의 나머지 전체를 추정할 수 있다고 설명하였다. 지진파 스펙트럼에서 가장 낮은 주파수 영역의 점근선을 지진 모멘트 M0으로 특정할 수 있다. 복사 에너지와 지진 모멘트 사이 관계를 응력 강하가 완벽하게 이뤄졌다고 가정하고 단층파괴 에너지를 무시한다면 다음과 같은 공식으로 정리할 수 있다.
여기서 E의 단위는 줄, M0의 단위는 Nm이며, 가나모리는 위 공식에서 모멘트 규모 Mw를 다음과 같이 계산하였다.
모멘트 규모[편집]
위의 공식은 에너지 기반 규모인 Mw를 더 쉽게 계산할 수 있도록 유도하였으나 이는 척도의 근본적인 성격을 모멘트 규모로 바꿔버렸다. 미국 지질조사국(USGS)의 지진학자인 토마스 C. 행크스는 가나모리가 만든 모멘트 규모 공식이 1973년 대처와 행크스가 언급했던 국지 규모 ML과 지진 모멘트 M0과의 관계[48]와 아주 유사하다고 언급하였다.
1979년 행크스와 가나모리는 지진 모멘트의 추정 공식에 기초하여 새로운 규모 단위를 정의하기 위해 두 논문의 성과를 하나로 합쳤다.[49]
여기서 는 뉴턴 미터(N·m) 단위이다.
현재 사용처[편집]
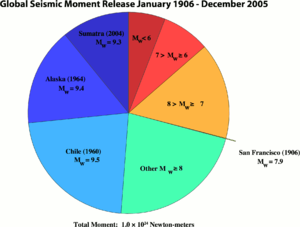
모멘트 규모는 현재 중대형 지진에서 지진의 규모를 측정하는 데 사용하는 가장 표준적인 규모 척도이지만,[50] 실제로는 지진 모멘트의 경우 매우 작은 규모인 경우 제대로 측정되지 않는 경우가 많기 때문에 모멘트 규모를 너무 작은 지진에서는 사용하기 곤란한 면이 있다. 예를 들어 미국 지질조사국에서는 모멘트 규모의 경우 규모 Mw5.0 이상인 경우에만 사용하며, 그 이하의 규모의 경우 국지 규모(릭터 규모) 같은 다른 규모를 사용하여 측정한다.[51]
또한 언론 등지에서도 규모 M4 이상의 지진이 발생했을 경우 규모 보도를 하는 편이다. 이런 중규모 이상의 지진인 경우 실제로는 모멘트 규모를 기준으로 기상기관이 발표하는 수치는 모멘트 규모로 나오지만 언론에서는 '리히터 규모' 혹은 '릭터 규모'라고 보도하는 경우가 많다.[52][3]
정의와 공식[편집]
모멘트 규모는 기호로 Mw로 나타내며, 여기서 아래첨자의 'w'는 기계적인 일을 나타내는 "work"의 약자이다. 가나모리 히로오가 처음 정의한 모멘트 규모는 아래의 공식으로 구하는 무차원량이다.
여기서 M0은 지진 모멘트로 그 단위는 다인 센치미터(10−7 N⋅m)이다.[53] 방정식에 있는 상수들은 국소 규모 및 표면파 규모와 같은 이전에 개발된 지진 규모와 그 값을 맞추고 일관성을 유지하기 위해 덧붙인 보정치이다. 따라서 규모 0의 미소지진은 1.2×109 N⋅m의 지진 모멘트를 가지며, 1960년 칠레 대지진 당시 모멘트 규모 M9.4-9.6의 지진 모멘트는 1.4×1023 N⋅m - 2.8×1023 N⋅m의 값이다.
규모와 에너지의 관계에서 규모가 1이 증가하게 되면 진폭은 10배정도 증가하고 에너지의 양은 약 32배 증가하게 된다. 한국지질자원연구원이 사용하는 모멘트 규모의 공식은 다음과 같다.[54]
: 표면파 진폭 : 표면파 주기 : 진앙거리 : 진원깊이 : 진원깊이 보정 계수 : 진앙거리 보정 계수
지진 모멘트, 방출된 퍼텐셜 에너지와 복사에너지 간의 관계[편집]
지진 모멘트는 지진이 발생하는 동안의 에너지 변화를 직접적으로 측정하여 구하지 않는다. 즉 지진 모멘트와 지진과 관련된 에너지 사이 관계는 오차가 매우 크고 지진마다 서로 달라질 수 있는 매개변수에 따라 크게 달라진다. 퍼텐셜 에너지는 축적된 변형력으로 인한 탄성 에너지와 중력 퍼텐셜 에너지의 형태로 지각 내에 쌓인다.[55] 지진이 발생하면 저장되어 있던 에너지 중의 일부인 가 다음과 같이 변환된다.
- 암반 균열을 만들어내는 과정에서 암반과의 마찰력을 이겨내고 비탄성 변형을 일으키며 소모된 에너지
- 열에너지
- 지진파로 복사된 에너지
지진으로 발생한 퍼텐셜 에너지의 강하는 지진 모멘트와 대략적으로 아래의 공식의 연관성이 존재한다.
여기서 는 지진 전후 단층의 절대전단응력의 평균값이며[56] 는 단층을 구성하는 암반의 전단 탄성 계수의 평균값이다. 현재까지 모든 관심있는 깊이에서 암반에 쌓인 응력의 절대값을 측정하는 기술이나 정확한 추정 방법은 존재하지 않기 때문에 의 값은 정확하게 알 수 없다. 이 값은 지진마다 크게 다를 수 있다. 지진 모멘트 M0이 같지만 이 다른 두 지진은 서로 다른 에너지 를 방출할 것이다.
지진의 복사 에너지는 지진 모멘트와 대략적으로 다음의 연관성이 존재한다.
여기서 는 복사 효율이며 는 정적 응력 강하, 즉 지진 전후 단층에 쌓인 전단 응력의 차이이다.[57] 이 두 양은 상수와는 거리가 멀다. 예를 들어 는 단층 파열 속도에 따라 크게 달라지는데 일반적인 지진의 경우 1에 가깝지만 해일지진이나 느린 지진의 경우 이 값이 1보다 작아진다. 지진 모멘트 M0가 같지만 나 가 다른 두 지진의 경우 도 서로 다르다.
와 은 근본적으로 진원과는 독립적인 성질을 가지고 있고 은 1970년대 들어서부터 직접적으로 확실하게 계산할 수 있게 되었기 때문에 복사 에너지와 연관된 또 다른 독립적인 지진 규모 척도를 정의할 수 있게 되었다. 1995년 초이와 보트와이트는 아래의 공식과 같은 '에너지 규모'를 정의하였다.[58]
여기서 는 J (N·m) 단위이다.
두 지진의 방출된 에너지 상대비[편집]
모든 지진에 대해 σ̄/μ가 동일하다고 가정할 때, 모멘트 규모 Mw는 지진으로 인한 퍼텐셜 에너지 변화량 ΔW의 척도로 볼 수 있다. 또한 모든 지진에 대해 가 동일하다고 가정하면 모멘트 규모 Mw는 지진으로 방사된 복사 에너지 Es의 측정값으로 볼 수 있다.[59][60]
위의 가정 하에서 모멘트 규모를 정의하는 방정식을 지진 모멘트 M0에 대해 푼 식을 정리하면 서로 다른 모멘트 규모 , 를 가진 지진의 방출 에너지(퍼텐셜 에너지 혹은 복사 에너지)의 비율 를 구할 수 있다.[61]
릭터 규모와 마찬가지로 모멘트 규모도 로그 척도를 따르므로 모멘트 규모가 1 증가하면 방출하는 에너지의 양이 101.5 ≈ 32배 증가하며, 모멘트 규모가 2 증가하면 에너지는 103 = 1000배 증가한다. 따라서 모멘트 규모 Mw7.0의 지진은 모멘트 규모 5.0 지진보다 에너지가 1,000배 강하며, 6.0 지진보다 약 32배 강하다.[62]
TNT 환산량과 비교[편집]
규모값을 절대적인 에너지 수치와 비교하기 위해 지진 발생시 방출되는 에너지를 기존의 화학 폭발물인 TNT의 세기와 비교하기도 한다. 지진 에너지 는 구텐베르크와 릭터의 공식에 따르면 아래와 같다.
이를 아래처럼 히로시마 원자폭탄 폭발력과도 비교할 수 있다.
줄 단위의 지진 에너지와 그에 해당하는 폭발 에너지를 비교하기 위해 TNT 1톤당 4.2 - 109의 환산량이 적용된다. 아래의 표는 지진의 에너지와 모멘트 규모, TNT 환산량간의 관계를 보여준다.[63]
| Mw | ES (줄) |
TNT- 환산량 (톤) |
히로시마 원자폭탄과 환산량 (12.5 kt TNT) |
|---|---|---|---|
| 3 | 2.0 · 109 | - | - |
| 4 | 6.3 · 1010 | 15 | 0.0012 |
| 5 | 2.0 · 1012 | 475 | 0.038 |
| 6 | 6.3 · 1013 | 15'000 | 1.2 |
| 7 | 2.0 · 1015 | 475'000 | 38 |
| 8 | 6.3 · 1016 | 15'000'000 | 1200 |
| 9 | 2.0 · 1018 | 475'000'000 | 38'000 |
| 10 | 6.3 · 1019 | 15'000'000'000 | 1200000 |
본 척도의 제일 끝 값은 10.6으로 이는 지구의 지각이 완전히 분해되었을 때 발생할 수 있을 것으로 가정되는 지진의 규모와 일치한다.[64]
파생 단위[편집]
모멘트 규모를 측정하기 위해 다양한 방법이 개발되었으며 모멘트 규모를 측정하는 방법에 따라 아래의 다양한 하위 파생 단위로 갈라진다.[65]
- Mwb - 주기 10초에서 100초의 장주기 실체파의 모멘트 텐서 역전에 기초하여 측정한다.
- Mwr - 국지적 거리(최대 1,800 km 이내)에서 측정한 지진파의 전체를 모멘트 텐서 역전하여 측정한다. RMT라고 부르기도 한다.
- Mwc - 중주기 혹은 장주기 실체파와 표면파의 센트로이드 모멘트 텐서 역전에 기초해 측정한다.
- Mww - W상(P파가 도착했을 당시 주기 100-1,000초가 넘는 초장주파의 상)에서 센트로이드 모멘트 텐서 역전에 기초해 측정한다.
- Mwp 혹은 Mi - 쓰보이 세이지[66]가 연안에 근접한 지역에서 일어난 거대지진의 쓰나미 위험성을 P파를 통해 빠르게 추정하기 위해 개발한 척도로, 나중에 통상적인 원거리 발생 지진에서도 쓰이게 확장되었다.[67]
- Mwpd - 단층 파열 지속시간을 고려한 지속시간-진폭 계산 척도로 Mw에서 볼 수 있는 것보다 더 오래 지속되는(=더 느린) 단층 파열로 방출한 에너지를 좀 더 정확하게 측정할 수 있다.[68]
같이 보기[편집]
각주[편집]
- ↑ Bormann, Wendt & Di Giacomo 2013, 86쪽.
- ↑ Bormann, Wendt & Di Giacomo 2013, 18쪽.
- ↑ 가 나 USGS Earthquake Magnitude Working Group이 만든 지진 규모 발표 기준 정책인 "USGS 지진 규모 정책"은 2002년 1월 18일 제정되었으며 다음 페이지에서 볼 수 있었다. 하지만 이 페이지는 웹 디자인 개정으로 사라졌으며 보존본은 Internet Archive의 다음 링크에서 볼 수 있다.
- ↑ Miyake 2017, 112쪽.
- ↑ Suzuki 2001, 121쪽. 또한 와다치의 지진 규모 관련 그래프는 Richter 1958의 Figure 2-22도 참조. (Bormann, Wendt & Di Giacomo 2013, 60쪽의 복사본)
- ↑ Gutenberg & Richter 1956a.
- ↑ Richter 1935.
- ↑ 총평에 대해서는 Bormann & Saul 2009 참조.
- ↑ Gutenberg 1945a.
- ↑ Gutenberg 1945b, Gutenberg & Richter 1956b.
- ↑ Kanamori 1977, 2981쪽.
- ↑ ISC-EHB Event 879136 [IRIS]. ISC-EHB Event 869809 [IRIS].
- ↑ Miyake 2017, 112–113쪽; Stauder 1962, 39쪽.
- ↑ Miyake 2017, 115쪽.
- ↑ Ben-Menahem 1995, 1210쪽; Maruyama 1963, 484쪽.
- ↑ Ben-Menahem 1995, 1210쪽.
- ↑ Miyake 2017, 115쪽.
- ↑ Miyake 2017, 115쪽. 당시 대부분 지진학자들이 단일결합설을 지지한 현대적, 학계적 설명에 대해서는 Byerly 1960를 참조.
- ↑ Miyake 2017, 116, 117쪽.
- ↑ Pujol 2003b, 164쪽.
- ↑ Pujol 2003b, 165쪽; Miyake 2017, 117–118쪽.
- ↑ Aki 1966b, 84쪽; Pujol 2003b, 167쪽.
- ↑ Julian, Miller & Foulger 1998, §2.2.1.
- ↑ Miyake 2017, 114, 117쪽; Maruyama 1963, 483쪽.
- ↑ Miyake 2017, 112쪽.
- ↑ Miyake 2017, 117쪽.
- ↑ Steketee 1958b, 1168–1169쪽.
- ↑ Stauder 1962, 42쪽; Aki & Richards 2002, 48쪽.
- ↑ Honda 1962, 32, 65쪽와 서지 참조; Ben-Menahem 1995, 1212쪽; Udías 1991, 90쪽; Maruyama 1963, 467쪽.
- ↑ Miyake 2017, 467쪽; Steketee 1958a, 1958b.
- ↑ 총망에 대해서는 Udías 1991에서 일부 참조.
- ↑ Pujol 2003b, 165, 167쪽; Miyake 2017, 118쪽.
- ↑ Bormann, Wendt & Di Giacomo 2013, 14쪽.
- ↑ Aki 1966b, 73쪽; Kassaras & Kapetanidis 2018, 410쪽.
- ↑ Beroza & Kanamori 2015, 5쪽.
- ↑ Dziewonski, Chou & Woodhouse 1981, 2826쪽; Aki 1966b.
- ↑ Aki 1966a, 24, 36쪽.
- ↑ Aki 1966a, 24쪽.
- ↑ Bormann, Wendt & Di Giacomo 2013, 12쪽, equation 3.1.
- ↑ Aki 1966b, 84쪽.
- ↑ Bormann, Wendt & Di Giacomo 2013, 14쪽; Bormann & Di Giacomo 2011, 412쪽.
- ↑ Bormann, Wendt & Di Giacomo 2013, 39–40쪽.
- ↑ Bormann, Wendt & Di Giacomo 2013, 7쪽.
- ↑ Abe 1982, 322쪽.
- ↑ Deichmann 2006, 1268쪽.
- ↑ Kanamori & Anderson 1975, 1076쪽.
- ↑ Kanamori 1977.
- ↑ Thatcher & Hanks 1973
- ↑ Hanks & Kanamori 1979
- ↑ Boyle 2008.
- ↑ “Magnitude Types”. 미국 지질조사국. 2022년 9월 28일에 확인함.
- ↑ Bormann, Wendt & Di Giacomo 2013, 86쪽
- ↑ Hanks & Kanamori 1979.
- ↑ “모멘트 규모”. 한국지질자원연구원.
- ↑ Kostrov 1974; Dahlen 1977.
- ↑ Venkataraman & Kanamori 2004 equation 3 참조.
- ↑ Venkataraman & Kanamori 2004 equation 1 참조.
- ↑ Choy & Boatwright 1995
- ↑ Kostrov, B. V. (1974). “Seismic moment and energy of earthquakes, and seismic flow of rock [in Russian]”. 《Izvestiya, Akademi Nauk, USSR, Physics of the solid earth [Earth Physics]》 1: 23–44 (English Trans. 12–21).
- ↑ Dahlen, F. A. (February 1977). “The balance of energy in earthquake faulting”. 《Geophysical Journal International》 48 (2): 239–261. doi:10.1111/j.1365-246X.1977.tb01298.x.
- ↑ Venkataraman, Anupama; Kanamori, H. (2004년 5월 11일). “Observational constraints on the fracture energy of subduction zone earthquakes” (PDF). 《Journal of Geophysical Research》 109 (B05302). Bibcode:2004JGRB..109.5302V. doi:10.1029/2003JB002549. 式3
- ↑ “1978-2000 지진관측보고” (PDF) (보도 자료). 대한민국 기상청. 2001년 3월. 8쪽. 2018년 9월 7일에 확인함.
- ↑ “FAQs – Measuring Earthquakes: How much energy is released in an earthquake?”. United States Geological Survey. 2010년 10월 27일에 원본 문서에서 보존된 문서. 2023년 6월 12일에 확인함.
- ↑ Quarks & Co. “Erdbeben – wenn die Erde zurückschlägt” (PDF). 2022년 3월 17일에 확인함.
- ↑ “Technical Terms used on Event Pages”. USGS. 2012년 5월 20일에 원본 문서에서 보존된 문서. 2023년 6월 12일에 확인함.
- ↑ Tsuboi 등. 1995.
- ↑ Bormann, Wendt & Di Giacomo 2013, §3.2.8.2, p. 135.
- ↑ Bormann, Wendt & Di Giacomo 2013, §3.2.8.3, pp. 137–128.
참고 문헌[편집]
- Abe, Katsuyuki (1982), “Magnitude, seismic moment and apparent stress for major deep earthquakes”, 《Journal of Physics of the Earth》 30 (4): 321–330, doi:10.4294/jpe1952.30.321, ISSN 1884-2305.
- Aki, Keiiti (1966a), “Generation and propagation of G waves from the Niigata earthquake of June 14, 1964. Part 1. A statistical analysis” (PDF), 《Bulletin of the Earthquake Research Institute》 44: 23–72.
- Aki, Keiiti (1966b), “Generation and propagation of G waves from the Niigata earthquake of June 14, 1964. Part 2. Estimation of earthquake moment, released energy and stress-strain drop from G wave spectrum” (PDF), 《Bulletin of the Earthquake Research Institute》 44: 73–88.
- Aki, Keiiti (April 1972), “Earthquake Mechanism”, 《Tectonophysics》 13 (1–4): 423–446, Bibcode:1972Tectp..13..423A, doi:10.1016/0040-1951(72)90032-7.
- Aki, Keiiti; Richards, Paul G. (2002), 《Quantitative Seismology》 2판, ISBN 0-935702-96-2.
- Ben-Menahem, Ari (August 1995), “A Concise Hiistory of Mainstream Seismology: Origins, Legacy, and Perspectives” (PDF), 《Bulletin of the Seismological Society of America》 85 (4): 1202–1225.
- Beroza, G. C.; Kanamori, Hiroo (2015), 〈4.01 Earthquake Seismologoy: An Introduction and Overview〉, Schubert, Gerald, 《Treatise on Geophysics》, 4: Earthquake Seismology 2판, doi:10.1016/B978-0-444-53802-4.00069-5, ISBN 9780444538024.
- Bormann; Di Giacomo (2011), “The moment magnitude Mw and the energy magnitude Me: common roots and differences”, 《Journal of Seismology》 15 (2): 411–427, Bibcode:2011JSeis..15..411B, doi:10.1007/s10950-010-9219-2, S2CID 130294359.
- Bormann, Peter; Saul, Joachim (2009), 〈Earthquake Magnitude〉 (PDF), 《Encyclopedia of Complexity and Applied Systems Science》 3, 2473–2496쪽.
- Bormann, Peter; Wendt, Siegfried; Di Giacomo, Dominico (2013), 〈Chapter 3: Seismic Sources and Source Parameters〉, Bormann, 《New Manual of Seismological Observatory Practice 2 (NMSOP-2)》, doi:10.2312/GFZ.NMSOP-2_ch3, 2019년 8월 4일에 원본 문서 (PDF)에서 보존된 문서, 2017년 8월 15일에 확인함.
- Boyle, Alan (2008년 5월 12일), 《Quakes by the numbers》, MSNBC, 2008년 5월 13일에 원본 문서에서 보존된 문서, 2008년 5월 12일에 확인함,
That original scale has been tweaked through the decades, and nowadays calling it the "Richter scale" is an anachronism. The most common measure is known simply as the moment magnitude scale.
.
- Byerly, Perry (1960년 5월 20일), “Earthquake Mechanisms”, 《Science》 131 (3412): 1493–1496, Bibcode:1960Sci...131.1493B, doi:10.1126/science.131.3412.1493, PMID 17802489.
- Choy, George L.; Boatwright, John L. (1995년 9월 10일), “Global patterns of radiated seismic energy and apparent stress”, 《Journal of Geophysical Research》 100 (B9): 18205–28, Bibcode:1995JGR...10018205C, doi:10.1029/95JB01969, 2011년 6월 6일에 원본 문서에서 보존된 문서, 2010년 3월 21일에 확인함.
- Dahlen, F. A. (February 1977), “The balance of energy in earthquake faulting”, 《Geophysical Journal International》 48 (2): 239–261, Bibcode:1977GeoJ...48..239D, doi:10.1111/j.1365-246X.1977.tb01298.x.
- Deichmann, Nicholas (August 2006), “Local Magnitude, a Moment Revisited”, 《Bulletin of the Seismological Society of America》 96 (4a): 1267–1277, Bibcode:2006BuSSA..96.1267D, CiteSeerX 10.1.1.993.2211, doi:10.1785/0120050115.
- Dziewonski; Chou; Woodhouse (1981년 4월 10일), “Determination of earthquake source parameters from waveform data for studies of global and regional seismicity” (PDF), 《Journal of Geophysical Research》 86 (B4): 2825–2852, Bibcode:1981JGR....86.2825D, doi:10.1029/JB086iB04p02825, 2019년 5월 7일에 원본 문서 (PDF)에서 보존된 문서, 2019년 5월 7일에 확인함.
- Dziewonski, Adam M.; Gilbert, Freeman (1976), “The effect of small aspherical perturbations on travel times and a re-examination of the corrections for ellipticity”, 《Geophysical Journal of the Royal Astronomical Society》 44 (1): 7–17, Bibcode:1976GeoJ...44....7D, doi:10.1111/j.1365-246X.1976.tb00271.x.
- Gutenberg, Beno (January 1945a), “Amplitudes of surface Waves and magnitudes of shallow earthquakes” (PDF), 《Bulletin of the Seismological Society of America》 35 (1): 3–12, Bibcode:1945BuSSA..35....3G, doi:10.1785/BSSA0350010003.
- Gutenberg, Beno (April 1945b), “Amplitudes of P, PP, and S and magnitude of shallow earthquakes” (PDF), 《Bulletin of the Seismological Society of America》 35 (2): 57–69, Bibcode:1945BuSSA..35...57G, doi:10.1785/BSSA0350020057.
- Gutenberg, Beno; Richter, Charles F. (April 1956a), “Earthquake magnitude, intensity, energy, and acceleration (Second Paper)” (PDF), 《Bulletin of the Seismological Society of America》 46 (2): 105–145, doi:10.1785/BSSA0460020105.
- Gutenberg, Beno; Richter, Charles F. (1956b), “Magnitude and energy of earthquakes”, 《Annali di Geofisica》 9 (1): 1–15.
- Hanks, Thomas C.; Kanamori, Hiroo (1979년 5월 10일), “A Moment magnitude scale” (PDF), 《Journal of Geophysical Research》 84 (B5): 2348–50, Bibcode:1979JGR....84.2348H, doi:10.1029/JB084iB05p02348, 2010년 8월 21일에 원본 문서 (PDF)에서 보존된 문서.
- Honda, Hirokichi (1962), “Earthquake Mechanism and Seismic Waves”, 《Journal of Physics of the Earth》 10 (2): 1–98, doi:10.4294/jpe1952.10.2_1.
- 국제지진센터, 《ISC-EHB Bulletin》, Thatcham, United Kingdom
- Julian, Bruce R.; Miller, Angus D.; Foulger, G. R. (November 1998), “Non-Double-Couple Earthquakes 1. Theory”, 《Reviews of Geophysics》 36 (4): 525–549, Bibcode:1998RvGeo..36..525J, doi:10.1029/98rg00716.
- Kanamori, Hiroo (1977년 7월 10일), “The energy release in great earthquakes” (PDF), 《Journal of Geophysical Research》 82 (20): 2981–2987, Bibcode:1977JGR....82.2981K, doi:10.1029/jb082i020p02981.
- Kanamori, Hiroo (1978년 2월 2일), “Quantification of Earthquakes” (PDF), 《Nature》 271 (5644): 411–414, Bibcode:1978Natur.271..411K, doi:10.1038/271411a0, S2CID 4185100.
- Kanamori, Hiroo; Anderson, Don L. (October 1975), “Theoretical basis of some empirical relations in seismology” (PDF), 《Bulletin of the Seismological Society of America》 65 (5): 1073–1095.
- Kassaras, Ioannis G.; Kapetanidis, Vasilis (2018), 〈Resolving the Tectonic Stress by the Inversion of Earthquake Focal Mechanisms. Application in the Region of Greece. A Tutorial〉, D'Amico, Sebastiano, 《Moment Tensor Solutions: A Useful Tool for Seismotectonics》, 405–452쪽, doi:10.1007/978-3-319-77359-9_19, ISBN 978-3-319-77358-2.
- Kostrov, B. V. (1974), “Seismic moment and energy of earthquakes, and seismic flow of rock [in Russian]”, 《Izvestiya, Akademi Nauk, USSR, Physics of the solid earth [Earth Physics]》 1: 23–44 (English Trans. 12–21).
- Maruyama, Takuo (January 1963), “On the force equivalents of dynamical elastic dislocations with reference to the earthquake mechanism”, 《Bulletin of the Earthquake Research Institute》 41: 467–486.
- Miyake, Teru (October–December 2017), “Magnitude, moment, and measurement: The seismic mechanism controversy and its resolution”, 《Studies in History and Philosophy of Science》, 65–66: 112–120, Bibcode:2017SHPSA..65..112M, doi:10.1016/j.shpsa.2017.02.002, hdl:10220/44522, PMID 29195644.
- Pujol, Josè (March–April 2003b), “The Body Force Equivalent to an Earthquake: A Tutorial”, 《Seismological Research Letters》 74 (2): 163–168, CiteSeerX 10.1.1.915.6064, doi:10.1785/gssrl.74.2.163.
- Richter, Charles F. (January 1935), “An Instrumental Earthquake Magnitude Scale” (PDF), 《Bulletin of the Seismological Society of America》 25 (1): 1–32, Bibcode:1935BuSSA..25....1R, doi:10.1785/BSSA0250010001, 2018년 7월 10일에 원본 문서 (PDF)에서 보존된 문서, 2022년 9월 10일에 확인함.
- Richter, Charles F. (1958), 《Elementary Seismology》, W. H. Freeman, ISBN 978-0716702115, LCCN 58-5970.
- Stauder, William (1962), 〈The Focal Mechanisms of Earthquakes〉, Landsberg, H. E.; Van Mieghem, J., 《Advances in Geophysics》 9, 1–76쪽, doi:10.1016/S0065-2687(08)60527-0, ISBN 9780120188093, LCCN 52-1226.
- Steketee, J.A. (1958a), “On Volterra's dislocations in a semi-infinite elastic medium”, 《Canadian Journal of Physics》 36 (2): 192–205, Bibcode:1958CaJPh..36..192S, doi:10.1139/p58-024.
- Steketee, J.A. (1958b), “Some geophysical applications of the elasticity theory of dislocations”, 《Canadian Journal of Physics》 36 (9): 1168–1198, Bibcode:1958CaJPh..36.1168S, doi:10.1139/p58-123.
- Suzuki, Yasumoto (June 2001), “Kiyoo Wadati and the path to the discovery of the intermediate-deep earthquake zone”, 《Episodes》 24 (2): 118–123, doi:10.18814/epiiugs/2001/v24i2/006, 2021년 2월 24일에 원본 문서에서 보존된 문서, 2022년 9월 10일에 확인함.
- Thatcher, Wayne; Hanks, Thomas C. (1973년 12월 10일), “Source parameters of southern California earthquakes”, 《Journal of Geophysical Research》 78 (35): 8547–8576, Bibcode:1973JGR....78.8547T, doi:10.1029/JB078i035p08547.
- Tsuboi, S.; Abe, K.; Takano, K.; Yamanaka, Y. (April 1995), “Rapid Determination of Mw from Broadband P Waveforms”, 《Bulletin of the Seismological Society of America》 85 (2): 606–613.
- Udías, Agustín (1991), “Source Mechanism of Earthquakes”, 《Advances in Geophysics》 33: 81–140, Bibcode:1991AdGeo..33...81U, doi:10.1016/S0065-2687(08)60441-0, ISBN 9780120188338.
- Utsu, T. (2002), Lee, W.H.K.; Kanamori, H.; Jennings, P.C.; Kisslinger, C., 편집., “Relationships between magnitude scales”, 《International Handbook of Earthquake and Engineering Seismology》, International Geophysics (Academic Press) A (81), 733–46쪽.
- Venkataraman, Anupama; Kanamori, H. (2004년 5월 11일), “Observational constraints on the fracture energy of subduction zone earthquakes” (PDF), 《Journal of Geophysical Research》 109 (B05302): B05302, Bibcode:2004JGRB..109.5302V, doi:10.1029/2003JB002549.
외부 링크[편집]
- 지진이야기 - 지진 규모 - 대한민국 지진연구센터
- (영어) USGS: Measuring earthquakes











![{\displaystyle M_{W}=\log[{\frac {A}{T}}]_{max}+1.66logB+3.3+M_{s}(h)+M_{s}(B)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7db24a000bffe6d30857413da69b0610634138f)


























