비틀어 늘린 쌍각뿔

비틀어 늘린 쌍각뿔의 집합
비틀어 늘린 오각쌍뿔은 정이십면체이다.
면	삼각형 4n개
모서리	6n
꼭짓점	2n+2
대칭군	Dnd, [2+,2n], (2*n), 4n차
회전군	Dn, [2,n]+, (22n), 2n차
쌍대다면체	깎은 엇쌍각뿔
특성	볼록

기하학에서 비틀어 늘린 쌍각뿔은 n각쌍뿔에 엇각기둥을 합동인 두 절반 사이에 넣음으로 "늘려"서 생성되는 무한한 다면체의 집합이다.

형태

이 집합의 둘은 삼각형 다면체이다. 즉, 완전히 정삼각형으로만 구성되었다: 존슨의 다면체인 비틀어 늘린 사각쌍뿔, 그리고 플라톤의 다면체인 정이십면체이다. 비틀어 늘린 삼각쌍뿔은 정삼각형으로 만들어질 수 있지만, 동일평면에 있는 면 때문에, 다시말해 엄밀히 볼록하지 않기 때문에 삼각형 다면체는 아니다. 삼각형들의 쌍은 마름모로 합쳐져서, 엇삼각쌍뿔로 볼 수 있다. 다른 것들은 이등변삼각형으로 만들 수 있다.

n	3	4	5	6	n
종류	평면	등변	정	평면
모양	비틀어 늘린 삼각쌍뿔	비틀어 늘린 사각쌍뿔	비틀어 늘린 오각쌍뿔 (정이십면체)	비틀어 늘린 육각쌍뿔	비틀어늘린 쌍뿔
그림
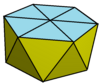
면	12	16	20	24	4n
쌍대	깎은 엇삼각쌍뿔	깎은 엇사각쌍뿔	깎은 엇오각쌍뿔 (정십이면체)	깎은 엇육각쌍뿔	깎은 엇쌍각뿔

같이 보기

• 늘린 쌍각뿔
• 비틀어 늘린 각뿔
• 늘린 각뿔
• 자른 엇쌍각뿔

외부 링크

• Conway Notation for Polyhedra Try: "knAn", where n=4,5,6... example "k5A5" is an icosahedron.