활동전위
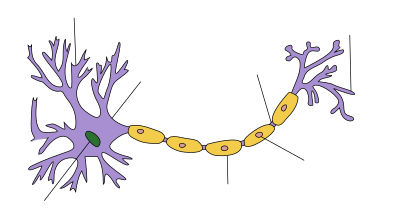
활동전위(活動電位, action potential; AP)는 근육·신경 등 흥분성 세포의 흥분에 따른 막 전위의 일시적 변화이다. 동작전위(動作電位)라고도 한다. 세포 안팎의 이온 조성은 세포막에 존재하는 나트륨·칼륨 등의 여러 이온 펌프의 활동에 의해 차이가 있는데, 이러한 이온 조성차로 세포막 안쪽이 60∼90 mV의 음전위(정지전위)를 나타낸다. 신경·근육 등의 흥분성 세포가 흥분하면 세포막 안팎의 극성이 바뀌어 세포내가 30∼40 mV의 양전위로 전위된다. 이러한 전위의 변화는 몇 밀리초(ms) 정도의 빠른 시간 안에 회복되므로 스파이크 전위(spike potential)라고도 하며, 회복기에 보이는 느린 변화인 후전위(after potential)와 구별된다. 이러한 전위의 변화에 따라 국소전류가 발생하여 1∼100m/s의 속도로 흥분이 전달된다. 이러한 전위의 변화를 율리우스 베른슈타인(Julius Bernstein)이 탈분극현상으로 설명하였다.
활동전위는 식물세포, 즉 끈끈이주걱·활수초 등에서도 보인다. 활동전위는 신경세포와 일부 신경내분비세포, 근세포에서 전기적 신호를 전달하는 방법으로 사용된다. 신경, 근육 등의 흥분성 세포가 신호를 받거나 스스로 흥분하면 분극상태의 세포막 투과성을 빠르게 변화시켜 막전위가 짧은 시간 동안 역전되면서 30~40 mV로 막전위가 탈분극된다. 이러한 전위변화는 수 밀리초(ms) 정도의 빠른 시간 안에 일어나고 회복된다. 활동전위는 휴지 상태로 돌아가기 전에 비활성 부위였던 인접부위에 전류를 보내고 새로운 활동전위를 생성하여 활동전위가 세포막 전체에 확산될 때까지 소실되지 않고 계속 전파된다.
활동전위는 크게 전압 개폐 나트륨 통로, 전압 개폐 칼륨 통로 및 다른 이온 채널에 의해 일어난다.
개관[편집]
동물, 식물, 균류의 세포막은 전위차(전압)를 유지하고, 이를 막전위라 한다. 동물 세포의 전형적인 막전위차는 -65 mV로, 1 V의 약 15분의 1에 해당한다. 세포막은 매우 얇기 때문에 막전위차는 세포막 안팎에 강한 전기력을 준다.
대부분의 세포에서 전압은 일정한 편이지만 전기적으로 활동적인 세포는 전압이 변화한다. 전압은 특정한 경우에 매우 빠르게 오르락내리락하고, 그 형태는 정형화된 양식을 따른다. 이 변화 주기를 활동전위라 한다. 활동전위가 지속되는 시간은 넓은 범위에 걸쳐 변화하여 결과적으로 아날로그 신호에 속한다. 동물의 뇌세포에서 변화는 ms 단위로 일어난다.[출처 필요] 기타 세포에서 변화 주기는 수 초에 걸쳐 일어날 수 있다.
동물세포의 전기적 특성은 막 구조에 의해 결정된다. 세포막은 단백질 분자가 박혀있는 지질층으로 이루어져 있다. 지질층은 전하를 띤 이온에 저항이 커서 부도체 기능을 한다. 반면에 막 단백질은 채널을 형성하여 이온이 막을 통과할 수 있게 한다. 몇몇 분자는 특정한 이온을 막 안팎으로 능동수송할 수 있다.
뉴런에서의 과정[편집]
동물의 신체 조직을 이루는 세포는 세포막 안팎으로 막 전위를 유지한다. 전기적 극성을 유지하는 것은 막에 박혀있는 이온 펌프와 이온 채널이다. 뉴런의 부분별로 막에 있는 이온 채널이 달라 가지돌기, 축삭, 세포체가 각각 전기적 특성이 다르다. 뉴런 어떤 부분의 막은 흥분성(활동전위를 생성할 수 있음)이고 어떤 부분은 그렇지 않다. 축삭 언덕(시작 마디, 축삭과 세포체가 만나는 부분) 뒤부터 흥분성 부위라는 연구 결과가 있으나,[출처 필요] 대부분의 사례에서는 세포체와 축삭 또한 흥분성이다.
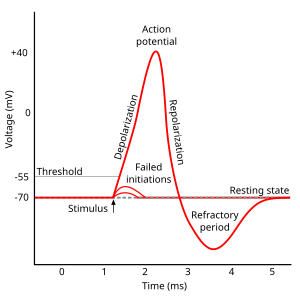
흥분성 막 부분에서 중요한 막 전위는 세포에 아무런 동요가 없을 때 막 전위인 휴지 전위와 그보다 높은 값인 역치 전위이다. 전형적인 뉴런 축삭 언덕에서 휴지 전위는 -70 mV, 역치 전위는 -55 mV 내외이다. 뉴런에 시냅스 자극이 오면 막은 탈분극(막 전위가 상승)이나 과분극(감소)한다. 활동전위는 막이 충분히 탈분극하여 역치까지 도달하면 일어난다. 역치를 넘어 탈분극이 일어나면 막 전위는 급격히 상승(+100 mV까지 도달하기도 한다)하고, 다시 급격히 감소하여 휴지 전위 아래까지 떨어졌다가 일정 시간 유지한 후 휴지 전위로 돌아온다. 활동전위의 형태는 일정하게 고정되어 있다. 즉 어떤 세포에서 활동전위는 같은 크기(amplitude)와 시간 주기로 일어난다(예외적인 경우를 이후에 다룸). 대부분의 뉴런에서 활동전위 전체 과정은 천 분의 일 초 내에 일어난다. 여러 뉴런이 초당 최대 10-100회의 속도로 활동전위를 일정하게 내보낸다. 그렇지 않은 뉴런은 수 분 이상 아무런 활동전위를 발생하지 않기도 한다.
생물물리학적 기초[편집]

활동전위는 세포막에 있는 특별한 전압 개폐 이온 채널에 의해 일어난다. 전압 개폐 이온 채널은 막에 박혀있는 단백질 집단으로 세 가지 특성을 지닌다.
- 한 개 이상의 입체형태를 가진다.
- 최소 한 개의 입체형태는 특정한 이온이 막을 통과하도록 한다.
- 한 입체형태에서 다른 입체형태로 전이(transition)는 막 전위의 영향을 받는다.
전압 개폐 이온 채널은 특정한 막 전위값에서 열리고 닫힌다. 대부분의 경우 막 전위와 채널 상태 사이의 관계는 확률론적이고 개폐에 시간차가 존재한다. 이온 채널은 입체형태를 예측할 수 없는 시각에 바꾼다. 막 전위는 전이 속도와 단위 시간당 각 입체형태일 확률을 결정한다.
전압 개폐 이온 채널은 양성 피드백 고리로 활동전위를 만들어낸다. 막 전위는 이온 채널의 상태를 통제하고 이온 채널은 막 전위를 통제한다. 따라서 특정 상황에서 막 전위가 올라가면 이온 채널이 열리고, 이로 인하여 막 전위가 더욱 상승한다. 활동전위는 양성 피드백 주기가 폭발적으로 진행될 때 일어난다. 활동전위의 시간과 크기 궤도는 활동전위를 생산하는 전압 개폐 이온 채널의 생물물리학적 특성이 결정한다. 다양한 채널이 활동 전위를 만들어내는 양성 피드백 기능을 한다. 전압 개폐 나트륨 채널은 신경 전도와 관련된 빠른 활동전위를 만든다. 근육 세포와 몇몇 뉴런에서 일어나는 느린 활동전위는 전압 개폐 칼슘 채널이 담당한다. 각각의 채널에는 전압 민감도와 시간에 따른 움직임이 다른 다수의 변형체(variant)가 존재한다.
가장 널리 연구되는 전압 의존성 이온 채널은 빠른 신경 전도에 관련된 나트륨 채널이다. 나트륨 채널과 활동전위의 생물물리학적 연구로 노벨상을 수상한 앨런 로이드 호지킨(Alan Hodgkin)과 앤드루 헉슬리Andrew Huxley)의 이름을 따 나트륨 채널을 호지킨-헉슬리 나트륨 채널이라고도 부르고, 더욱 단순하게는 NaV 채널(V는 전압을 의미)이라고 부른다. NaV 채널은 불활성형(deactivated state), 활성형(activated state), 차단형(inactivated state) 등 세 가지 상태로 존재할 수 있다. 채널은 활성형 상태일 때 나트륨 이온에 대해서만 투과성이 있다. 막 전위가 낮을 때 채널은 대부분의 시간 동안 불활성형(닫힌형) 형으로 존재한다. 막 전위가 특정 수준 이상으로 올라가면 채널이 활성형(열린형)으로 전이될 확률이 증가하고, 막 전위가 높을수록 확률은 더 커진다. 채널이 활성화되고 나면 차단형(닫힌형)으로 변화하고, 그 상태로 일정 시간 유지된다. 막 전위가 다시 낮아지면 채널은 불활성형(닫힌형)으로 돌아간다. 결론적으로 활동전위 동안 채널이 거치는 주기는 불활성형 → 활성형 → 차단형 → 불활성형 순이다. 이 순서는 채널 전체를 기준으로 평균적인 행동이고, 이론적으로 각각의 채널은 한 시점에서 전이 상태가 모두 다를 수 있다. 다만 채널이 차단형에서 곧바로 활성형으로 바뀌는 것은 거의 일어나지 않는다. 차단형에 있는 채널은 불활성형으로 되돌아갈 때까지 불응기(무반응성, refractory)를 거친다.
이러한 NaV의 동역학적 특성의 결과 NaV는 천이 매트릭스(transition matrix)의 지배를 받는다. 채널 자체가 전압을 결정하는 중요 역할을 하기 때문에, 채널이 존재하는 계의 전체적인 동역학을 계산하기는 상당히 어렵다. 호지킨과 헉슬리는 이온 채널의 상태를 나타내는 매개변수(parameter)에 대한 미분 방정식, 호지킨-헉슬리 방정식을 세웠다. 호지킨-헉슬리 방정식은 계속 변형되었지만 활동전위를 연구하는 생물물리학의 이론적인 출발점이 되고 있다.
막 전위가 올라감에 따라 나트륨 이온 채널이 열려 세포 내로 나트륨 이온이 들어온다. 칼륨 이온 채널이 그 뒤를 이어 열려 칼륨 이온이 세포 바깥으로 빠져나간다. 나트륨 이온의 유입은 양전하를 띤 양이온의 농도를 증가시켜 휴지 전위보다 높은 전위 상태인 탈분극을 유발한다. 활동전위가 최고에 달했을 때 나트륨 채널은 닫히고 칼륨 채널은 계속해서 열려있어 칼륨이 세포 밖으로 나간다. 칼륨 이온의 유출로 막 전위가 감소하고 세포는 과분극된다. 이 지점에서는 칼륨 흐름이 나트륨 보다 많아 전위는 약간 상승하고 정상적인 휴지 전위(대개 -70 mV)에 도달한다.[1][2][3] 휴지 전위보다 15 mV 높은 역치 전위를 지나 더 상승하면 나트륨 흐름이 더 우세하다. 그 결과 양성 피드백으로 나트륨 흐름은 나트륨 채널을 더 많이 활성화한다. 따라서 세포는 발화하여 활동 전위를 만든다.[1][4][5][note 1] 세포의 활동전위가 발생하는 빈도를 발화율이라 한다.
전압 개폐 채널을 열어서 생기는 이온의 흐름은 대개 활동전위를 만드는 초기 흐름보다 크다. 따라서 활동전위의 크기와 지속 시간, 형태는 자극의 크기나 지속 시간이 아니라 흥분하는 막의 특성에 대부분 의존한다. 이러한 실무율 특성은 수용기 전위, 전기긴장성 전위, 시냅스 전위 등 자극의 세기에 따라 증감하는 다단계 전위와 구별된다. 활동전위는 전위 개폐 채널과 유출 채널(leak channel)의 종류, 채널 분포, 이온 농도, 막 전기 용량, 온도 및 기타 요소에 따라 다양하다.
활동전위에 관여하는 주요 이온은 나트륨과 칼륨 양이온이다. 나트륨 이온은 세포 안으로, 칼륨 이온은 세포 밖으로 이동하여 평형을 유지한다. 상대적으로 적은 이온 이동만으로도 막 전위를 극적으로 변화시킬 수 있다. 따라서 활동전위 동안 이온 교환으로 변하는 막 안팎의 이온 농도는 무시할 수 있다. 막을 건너는 이온 중 소수는 다른 이온 수송체와 함께 정상 이온 농도비를 유지하는 나트륨-칼륨 펌프에 의하여 다시 되돌아간다. 칼슘 양이온과 염소 음이온은 심장 활동전위와 단세포 조류 Acetabularia의 활동전위 등 소수의 활동전위 유형과 연관이 있다.
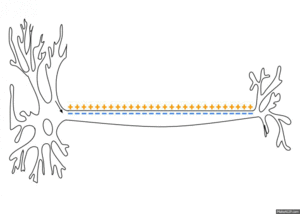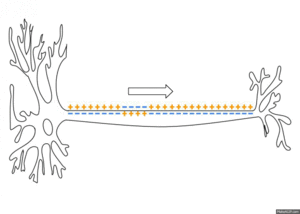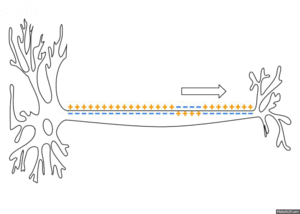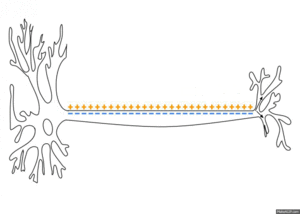
활동전위는 막의 흥분성 부분에서 국소적으로 만들어지지만, 휴지 상태의 이온 흐름도 인접한 막의 연장선에서 활동전위를 유발하고 도미노처럼 퍼지게 할 수 있다. 수동적으로 퍼지는 전기긴장성 전위와 반대로, 활동전위는 흥분이 막을 따라 뻗어가면서 계속 새로 만들어지고, 감소하지 않는다.[6] 축삭에서 수초가 있는 부분은 흥분성이 아니고 활동전위를 만들지 않아 신호가 전기긴장성 전위처럼 수동적으로 전파된다. 일정한 간격으로 수초가 없는 부분, 즉 랑비에결절은 활동전위를 만들고 신호를 빠르게 도약 전도한다. 도약 전도는 축삭 지름이 작아도 신호의 속도를 높여주는 효과가 있다. 축삭 말단이 탈분극되면 신경전달물질이 시냅스 틈으로 방출된다. 신피질 어디에나 존재하는 피라미드 뉴런의 가지돌기에서는 활동전위가 거꾸로 전파되기도 하는데,[a] 이 현상은 돌기-시기 의존성 가소성에 영향을 미치는 것으로 추정된다.
신경전달[편집]
뉴런 해부학[편집]
| 뉴런 |
|---|
활동전위를 갖는 세포로는 식물 세포, 근육 세포, 심장의 일부 특수한 세포(심장 활동전위가 일어나는 세포) 등이 있지만, 주요 흥분성 세포는 뉴런이다. 뉴런은 가장 간단한 활동전위 기작을 가진다.
뉴런은 전기적으로 흥분하는 세포로 대개는 한 개 이상의 가지돌기를 가지고 있고, 단일 세포체와 축삭, 하나 이상의 축삭 말단으로 이루어져 있다. 가지돌기는 세포에서 뻗어나온 돌기이고, 일차적으로는 시냅스 신호를 받는 역할을 한다. 가지돌기에서 돌출된 가시는 시냅스전 뉴런에서 방출되는 신경전달물질을 포착할 수 있게 되어 있다. 가시에는 리간드 개폐 이온 채널이 많다. 가시는 가느다란 '목'으로 망울 형태의 돌출부에 연결된다. 이런 구조적 특성으로 인하여 가시 안에서 일어나는 변화가 이웃한 가시에 영향을 줄 확률이 줄어든다. 극소의 예외(장기 강화)는 있지만, 가지돌기의 가시는 독립적인 단위로 행동한다. 가지돌기는 세포핵이 있는 세포체와 대부분의 세포소기관에서 멀리 뻗어나온 형태이다. 세포체의 표면에는 가시와 달리 전압 활성 이온 채널이 많이 있다. 이 채널은 가지돌기에서 만들어진 신호를 전달하는 것을 돕는다. 세포체에서 축삭으로 나오는 부분이 축삭 언덕이다. 축삭 언덕은 전압 활성 나트륨 채널이 밀집되어 있는 것이 특징이다. 일반적으로 축삭 언덕을 활동전위가 급등하여 시작되는 영역으로 간주한다.[7] 가시에서 생성되고 세포체로 전달된 신호는 모두 축삭 언덕으로 모인다. 축삭 언덕에서 곧장 이어진 부분이 축삭이다. 축삭은 관 형태로 세포체에서 길게 뻗어 있고, 미엘린 수초로 절연되어 있다. 미엘린은 신경아교세포의 일종인 슈반 세포(말초신경계의 경우)나 희소돌기아교세포(중추신경계)로 이루어져 있다. 신경아교세포는 전기적 신호 전달에 관여하지 않지만, 서로 소통하여 뉴런에 중요한 생화학적 도움을 준다.[8] 미엘린은 축삭 분절을 여러번 감싸 두꺼운 지방층을 형성하고 이온이 축삭으로 들어오거나 축삭을 빠져나가는 것을 막는다(절연). 절연을 통하여 신호가 감소하지 않고 전달 속도를 유지할 수 있지만, 절연 부위에는 채널이 존재할 수 없다. 축삭의 막에는 일정한 간격으로 절연되지 않은 부위, 랑비에결절이 있다. 랑비에결절은 일종의 축삭 언덕처럼 작용하여 신호가 감소하지 않도록 증폭시킨다. 축삭의 끝부분은 절연이 벗겨지고 여러 갈래로 나뉘어 축삭 말단을 형성한다. 이들이 시냅스전 말단 혹은 시냅스 단추(synaptic bouton)로, 신경전달물질이 든 작은 막 구조물인 시냅스 소포가 여기 존재한다.
개시[편집]
활동전위가 시작되기 위해서는 축삭 언덕에서 막전위가 역치보다 증가하여야 한다.[1][2][9][10] 탈분극이 일어나는 데에는 여러 방법이 있다.

동역학[편집]
활동전위는 일반적으로 시냅스전 뉴런에서 온 흥분성 시냅스후 전위에 의해서 시작된다.[11] 신경전달물질 분자는 시냅스전 뉴런에서 방출되어 시냅스후 세포의 수용체에 결합하고, 그 결과 다양한 이온 채널이 열린다. 이온 채널이 열리면 세포막 투과성이 국소적으로 변화하고 따라서 막 전위가 변한다. 신경전달물질이 수용체에 결합하여 전압을 증가시키면(막이 탈분극) 시냅스는 흥분한다. 반대로 전압을 감소시키면(막이 과분극) 시냅스는 억제된다. 전압의 변화는 케이블 방정식(cable equation, #케이블 이론)이 설명하는 바와 같이 수동적으로 인접한 막 영역으로 전파된다. 전압 자극은 시냅스와의 거리 및 신경전달물질이 결합하는 시간에 따라 지수적으로 감소한다. 대개는 흥분성 전압의 일부만 축삭 언덕에 닿고 막을 탈분극시켜 드물게 새로운 활동전위를 일으킨다. 가장 일반적으로는 여러 시냅스에서 온 흥분성 전위가 거의 동시에 함께 작용하여 새로운 활동전위를 일으키고, 억제성 시냅스후 전위는 반대작용을 하여 활동전위가 생성되는 것을 방해한다.
신경전달은 전기적 시냅스 사이에서도 일어난다.[12] 세포 사이에 흐르는 자유로운 이온을 통하여 화합물이 관여하지 않고 빠른 전달이 가능하다. 흥분성 세포가 틈새이음을 통하여 직접 연결되어 있기 때문에 활동전위는 세포 사이에 양방향으로 직접 전달된다. 정류 시냅스(rectifying synapse)라는 일부 전기적 시냅스에서는 활동전위가 한 방향으로만 이동한다.[13] 전기적 시냅스는 화학적 시냅스보다 드물기는 하지만 사람의 뇌를 포함하여 신경계 전반에 존재한다.[14]
실무율 원리[편집]
활동전위의 크기는 전위를 생성하는 전류의 세기와 무관하다. 즉 이온 흐름이 많을수록 활동전위가 커지지는 않는다. 활동전위는 완전히 일어나거나 아예 일어나지 않거나 둘 중 하나이고,[b][c][d] 이러한 특성을 실무율(all-or-none)이라고 한다. 활동전위의 빈도는 자극의 세기와 관련이 있다. 이와 대조적으로, 수용기 전위의 경우 전위 크기가 자극의 세기에 의존한다.[15]
감각 뉴런[편집]
감각 뉴런의 외부 신호는 압력, 온도, 빛, 소리이다. 외부 신호는 이온 채널을 여닫아 이온에 대한 막의 투과성과 막 전위를 변화시킨다.[16] 전압 변화는 흥분성(탈분극) 혹은 억제성(과분극)으로, 두 전위의 합에 따라 축삭 언덕을 탈분극시켜 활동전위를 일으킨다. 이렇게 활동전위를 일으키는 감각 뉴런의 예로 사람의 후각 수용기(후각)와 마이스너 소체(촉각)가 있다. 모든 감각 뉴런이 외부 신호를 활동전위로 전환하는 것은 아니다.[17] 외부 신호를 받으면 신경전달물질을 방출하거나 연속적인 차등 전위를 통하여 다음 뉴런에 전달하고, 그 뉴런이 활동전위를 생성한다. 사람의 귀에 있는 털세포는 소리 신호가 오면 기계 개폐 이온 채널을 여닫아서 신경전달물질을 방출한다. 사람의 망막에 있는 빛수용기 세포와 그 다음 층을 이루는 두극세포, 수평세포는 활동전위를 생성하지 않는다. 아마크린 세포 일부와 망막 신경절세포가 있는 제3층에서는 활동전위를 생성하고, 전위가 시신경으로 이동한다.
박동조율기 전위[편집]
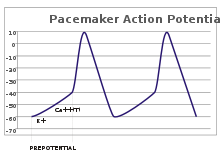
감각 뉴런처럼 외부 자극에 대하여 활동전위를 일으키는 것과는 달리, 아무런 자극 없이 발화하는 흥분성 세포가 있다. 이들은 규칙적인 속도로 축삭 언덕에서 자발적으로 탈분극하여 시계처럼 작용한다.[18] 이 세포의 전압 변화를 박동조율기 전위라고 한다.[19] 심장의 굴심방결절에 있는 심장 박동조율기 세포가 이에 속한다.[e] 박동조율기 전위는 자연적인 리듬을 가지고 있지만 외부 자극에 의해 조절될 수도 있다. 예를 들어 심박수는 약물이나 교감 및 부교감신경에 의해 변화한다.[20] 외부 자극은 세포가 반복적으로 발화하도록 하는 것이 아니라 자연적으로 발화하는 시간을 조절한다.[19] 발화 빈도는 복잡하게 조절되고, 돌발적인 활동전위 패턴(bursting)을 만들기도 한다.
활동전위의 각 시기[편집]
활동전위 시기는 다섯 부분, 즉 상승기, 최고기(peak phase), 하강기, 후기 과분극기(undershoot phase 혹은 after-hyperpolarization), 불응기로 나뉜다. 상승기에는 막 전위가 +쪽으로 이동하여 탈분극된다. 탈분극이 멈추는 지점을 최고기라고 한다. 이 단계에서 막 전위는 최고에 달한다. 이어지는 시기가 하강기로, 막 전위가 -쪽으로 이동하여 휴지 전위에 근접한다. 후기 과분극기는 막 전위가 일시적으로 휴지 전위보다 낮은(-상태, 과분극) 시기이다. 마지막으로 다음 활동전위가 발화할 수 없는, 혹은 발화하기 힘든 시기인 불응기가 이어진다. 불응기는 다른 시기와 겹칠 수 있다.[21]
활동전위 과정은 두 개의 짝지은 에 의해 결정된다.[22] 첫째, 전압 민감성 이온 채널이 막 전위 Vm의 변화에 따라 열리고 닫혀 이온 투과성이 변화한다.[23] 둘째, 골드만 방정식에 따르면 막 투과성은 평형 전위 Em에 따라 변하므로 따라서 막 전위 Vm에 따라서 변하는 것이 된다.[f] 막 전위는 투과성에 영향을, 투과성은 막 전위에 영향을 미친다. 이런 양성 피드백이 상승기의 주요 요소이다.[1][4] 하나의 이온 채널이 Vm의 변화에 따라 반대로 행동하거나 다른 속도로 작용하는 다수의 "문"을 가지고 있다면 상황이 복잡해진다.[24][g] 예를 들어 Vm가 상승하면 전압 민감성 나트륨 채널의 문 대부분이 열리지만, 채널의 "불활성화 문(inactivation gate)"은 느리게라도 닫힌다.[25] 따라서 Vm이 갑자기 상승하면 나트륨 채널은 초기에는 열리지만, 느린 불활성화에 의해 결국 닫히게 된다.
활동전위의 전압과 전류에 대한 정확한 모형은 앨런 로이드 호지킨과 앤드루 헉슬리가 1952년에 만들었고,[g] 그 공로로 1963년 노벨 생리학·의학상을 수상하였다.[lower-greek 2] 이 모형은 전압 민감성 이온 채널 단 두 종만을 고려하고, 내부적인 문(gate)은 서로에게 독립적으로 여닫힌다고 가정하였다. 실제로는 이온 채널의 종류가 더 많으며[26] 반드시 독립적으로 여닫히는 것은 아니다.[h]
자극과 상승기[편집]
활동전위는 자극이 Vm을 증가시켜 충분히 강한 탈분극이 있을 때 축삭 언덕에서 시작한다.[27] 세포에 나트륨 양이온이 유입되면 탈분극이 일어난다. 나트륨 양이온은 화학적 시냅스, 감각 뉴런, 박동조율기 전위 등 다양한 곳에서 온다.
휴지기에 있는 뉴런의 세포외액에는 나트륨과 염소 이온 농도가 높고, 세포내액에는 칼륨 이온 농도가 높다. 막 안팎의 이온 농도 기울기와 막에 있는 칼륨 누출 채널은 칼륨 이온이 세포 밖으로 빠져나가게 하여 휴지 전위 EK는 약 –75 mV를 유지한다.[28] 막이 탈분극되면 나트륨과 칼륨 채널이 모두 열려 나트륨은 축삭 안으로, 칼륨은 바깥으로 이동한다. 탈분극 정도가 작으면(예: Vm가 -70 mV에서 -60 mV로 증가), 바깥으로 나가는 칼륨이 안으로 들어오는 나트륨보다 많아 막이 다시 정상적인 휴지 전위(-70 mV 근처)로 돌아온다(재분극).[1][2][3] 탈분극이 충분히 크면 안으로 들어오는 나트륨이 바깥으로 나가는 칼륨보다 많아 양성 피드백이 일어난다. 즉, 안으로 들어오는 이온이 많을수록 Vm가 더욱 증가하고, 그 결과 안으로 들어오는 이온이 더 많아진다.[1][4] 충분히 강한 탈분극(Vm 증가)은 전압 민감성 나트륨 채널을 열고, 나트륨 이온의 투과성이 높아지면 Vm은 나트륨 평형 전압인 ENa≈ +55 mV에 근접한다. 전압이 증가하면 나트륨 채널을 더 많이 열어 Vm이 ENa에 가까워지도록 더 밀어붙이고, 모든 나트륨 채널이 열릴 때까지 계속된다.[1][2][9][10] Vm과 나트륨 투과성이 가파르게 증가하는 이 시기가 활동전위의 상승기에 해당한다.[1][2][9][10]
양성 피드백(또는 runaway condition)이 일어나는 임계 역치 전압은 -45 mV 전후이지만, 축삭의 활성 상태에 따라 달라진다. 갓 발화한 막은 이온 채널이 불활성형으로 돌아올 때까지 다른 활동전위를 만들 수 없다. 이 시기가 절대적 불응기이다.[29][30][31] 절대적 불응기가 지나고 몇몇 이온 채널은 불활성형으로 회복되면 축삭은 다른 활동전위를 생성할 수 있지만, 역치가 더 높아져 더욱 강력한 탈분극(예컨대 -30 mV)이 필요하다. 이례적으로 활동전위가 만들어지기 어려운 이 시기를 상대적 불응기라 한다.[29][30][31]
최고점 및 하강기[편집]
상승기의 양성 피드백은 나트륨 이온 채널이 최대로 열리면서 점차 느려져 정지한다. 활동전위의 최고점에서 나트륨 투과성은 최대가 되고 막 전압 Vm은 거의 나트륨 평형 전압 ENa와 같아진다. 처음에는 나트륨 채널을 열었던 전압 상승이 이제는 나트륨 채널을 천천히 닫는 역할을 한다. 나트륨 채널의 구멍이 닫히고 차단형으로 전환된다.[25] 이로 인하여 나트륨이 칼륨에 비하여 상대적으로 막 투과성이 낮아지고 막 전압이 휴지 전위값으로 되돌아간다. 동시에 높아진 전압은 전압 민감성 칼륨 채널을 열고, 칼륨 막 투과성이 높아지면 Vm은 EK를 항해 변한다.[25] 나트륨 및 칼륨 투과성 변화가 종합적으로 Vm을 빠르게 떨어뜨리고 막은 재분극되면서 활동전위는 하강기에 접어든다.[29][32][10][33]
후기 과분극[편집]
올라간 전압은 칼륨 채널을 평소보다 더 많이 열고, 칼륨 채널 중 일부는 막이 평소의 휴지 전압으로 돌아가도 곧바로 닫히지 않는다. 또한 활동전위 동안 유입된 칼슘 이온에 반응하여 SK 채널이 추가적으로 열린다. 칼륨의 투과성은 일시적으로 매우 높아지고 막 전위 Vm는 칼륨 평형 전위인 EK에 더욱 가까워진다. 이로 인하여 과분극이 일어나고 이를 후기 과분극(afterhyperpolarization 혹은 undershoot)이라 한다. 칼륨 투과성이 원래 값으로 회복되면 정상 휴지 전위값으로 돌아온다.[34][32]
불응기[편집]
활동전위에는 매번 불응기가 따른다. 불응기는 새로운 활동전위가 전혀 일어나지 못하는 절대적 불응기와 평소보다 강한 자극이 필요한 상대적 불응기로 나뉜다.[29][30][31] 불응기는 나트륨과 칼륨 채널 분자의 상태 변화로 인하여 생긴다. 활동전위가 끝날 때 나트륨 채널은 차단형(inactivated state)이 되면서 닫힌다. 차단형 나트륨 채널은 막 전위에 관계없이 열릴 수 없는 상태로 이 시기가 절대적 불응기에 해당한다. 충분히 많은 나트륨 채널이 휴지 상태로 전이한 뒤에도 칼륨 채널 중 일부는 여전히 열려 있어 막 전위가 탈분극되기 어렵다. 이 시기가 상대적 불응기에 해당한다. 칼륨 채널의 밀도와 아형은 뉴런 종류에 따라 크게 다르기 때문에 상대적 불응기 지속 시간도 차이가 크다.
절대적 불응기가 있어서 활동전위는 축삭을 따라 한 방향으로만 전파된다.[35] 어떤 특정한 순간에 활동전위가 치솟는 부분 바로 뒤의 축삭은 불응기이고, 앞쪽은 활동전위를 일으킨 적이 없어서 불응기에 있지 않기 때문에 탈분극에 의해 활성화될 수 있다.
전도[편집]
활동전위는 축삭 언덕에서 생성되어 축삭을 따라 파동처럼 전파된다.[36] 활동전위 동안 축삭의 한 지점에서 들어오는 이온 흐름은 축삭을 따라 퍼지면서 인접한 막을 탈분극 시킨다. 탈분극이 충분히 강하면 이웃 막 부분에서도 활동전위를 일으킨다. 활동전위가 퍼지는 기초적인 기작은 앨런 로이드 호지킨이 1937년에 증명한다. 신경 절편을 부수거나 냉각시켜 활동전위를 차단한 뒤에, 차단 분절이 충분이 짧으면 차단 부위 한 쪽에 도달한 활동전위가 반대편에서 활동전위를 일으킬 수 있다는 것을 보였다.[i]
막 일부에서 활동전위가 일어나면 다시 발화하기 전에 막이 회복되는 시간이 필요하다(불응기). 분자 수준에서 절대적 불응기는 전압 활성 나트륨 채널이 차단형에서 회복되어 닫힌형(불활성형)으로 돌아오는데 드는 시간에 해당한다.[30] 뉴런에는 다양한 전압 활성 칼륨 채널이 존재한다. 몇몇은 빨리 차단형으로 전이되고, 몇몇은 천천히 차단형으로 전이되거나 아예 전이되지 않는다. 이런 다양성으로 인하여 칼륨 채널 일부가 탈분극이 진행되면서 차단형이 되어도 항상 막이 재분극될 수 있는 칼륨 이온 흐름이 존재한다. 반면에 뉴런에 있는 모든 전압 활성 나트륨 채널은 강한 탈분극이 일어나고 수 ms 이내에 차단형으로 전이된다. 나트륨 채널 상당수가 불활성형으로 돌아오기 전에는 다시 탈분극할 수 없다. 절대적 불응기는 발화 빈도를 제한하지만[37] 축삭을 따라 활동전위가 한 방향으로만 전달되게 한다.[35] 본래 활동전위에서 이온 흐름은 양방향으로 전파된다.[38] 그러나 이미 발화되지 않은 축삭만이 활동전위에 반응할 수 있고, 갓 발화한 부분은 활동전위가 확실하게 그 범위를 벗어나서 그 부분을 다시 자극할 수 없을 때까지 반응하지 않는다. 활동전위가 축삭 언덕에서 축삭 말단의 시냅스 단추(synaptic knob, 종말단추)로 전파되는 순방향성 전도(orthodromic conduction)가 일반적이며, 반대 방향으로 전파되는 역방향성 전도(antidromic conduction)는 매우 드물다.[39] 실험실에서 인위적으로 축삭 가운데 지점을 자극하면 축삭의 양쪽 반이 모두 발화하지 않은 상태이므로 활동전위는 양방향으로 생성되어 하나는 축삭 언덕으로, 다른 하나는 시냅스 단추를 향하여 진행한다.
수초 및 도약 전도[편집]

신경계에서 전기 신호를 빠르고 효율적으로 전달하기 위한 장치가 특정 뉴런에 있는 미엘린 수초이다. 미엘린은 여러 층으로 된 막으로 중간중간 랑비에결절이라는 부분을 제외하고 축삭을 감싼다. 미엘린은 특수한 세포에서 생산된다. 말초신경계에서는 슈반 세포가, 중추신경계에서는 희소돌기아교세포가 그 역할을 담당한다. 미엘린 수초는 막 전기 용량을 감소시키고 랑비에결절 사이의 저항을 증가시켜서 활동전위가 결절에서 결절로 빠르게 도약하도록 한다.[j][k][l] 미엘린 형성은 주로 척추동물에서 나타나며, 새우 같은 십각목 갑각류에 속하는 소수의 무척추동물도 유사한 체계를 갖추고 있다.[m] 척추동물의 모든 뉴런이 수초를 가지지는 않는다. 자율신경계를 구성하는 뉴런의 축삭은 일반적으로 수초가 없다.
미엘린은 이온이 축삭으로 들어오거나 빠져 나가는 것을 막는다. 수초가 있는 뉴런은 일반적으로 전도가 빠르고 에너지 측면에서 효율적이다. 도약 전도와 관계없이 활동전위의 평균 신경 전달 속도는 1 m/s에서 100 m/s 이상으로, 일반적으로는 축삭 지름이 커질수록 속도도 증가한다.[n]
활동전위는 수초가 있는 축삭 분절의 막에는 퍼질 수 없다. 랑비에결절 한두 개를 탈분극시킬 수 있는 이온 흐름은 세포질을 타고 이동한다. 한 결절에서 활동전위를 일으킨 흐름은 다음 결절에서도 활동전위를 일으킨다. 이렇게 결절에서 결절로 활동전위가 "깡총깡총" 이동하는 것을 도약 전도라 한다. 도약전도 기작은 1925년 랄프 릴리(Ralph Lillie)가 제안하였으나,[o] 실험 증거는 타사키 이치지(일본어: 田崎 一二)[p]와 타케우치 타이지[q][40], 앤드루 헉슬리와 로베르트 슈템플리(독일어: Robert Stämpfli)[r]가 처음 제시하였다. 수초가 없는 축삭에서 활동전위는 바로 인접한 막을 탈분극시키고 축삭을 따라 파동처럼 이동한다.

수초가 있는 축삭은 보다 빠르게 전도할 수 있고 에너지 효율이 좋다는 장점이 있다. 최소 지름(약 1 μm)보다 큰 축삭은 수초가 많을수록 활동전위의 전도 속도가 약 10배 증가한다.[t] 반대로 생각하면 주어진 전도 속도에서 수초가 있는 뉴런은 수초가 없는 뉴런에 비하여 지름이 더 작다. 예를 들어 활동전위는 수초가 있는 개구리 축삭과 수초가 없는 오징어의 거대 축삭에서 유사한 속도(약 25 m/s)로 이동하지만, 개구리의 축삭은 지름은 30분의 1 수준이고 단면적은 1000배나 작다. 이온 흐름이 랑비에결절에만 국한되기 때문에 막 안팎으로 새나가는 이온이 훨씬 줄어들어 대사 에너지를 절감하는 효과도 있다. 사람 신경계는 전신 대사 에너지의 약 20%를 소모하기 때문에[t] 이 효과는 자연선택에서 중요한 장점으로 작용한다.
축삭의 수초가 있는 분절의 길이는 도약 전도에 중요한 요소이다. 전도의 속도를 극대화할 수 있는 만큼 길어야 하고 그렇다고 다음 랑비에결절에서 활동전위를 일으키지 못할 정도로 신호가 약해져서는 안 된다. 자연계에 존재하는 수초 분절은 수동적으로 전파된 신호가 최소 두 개 결절까지 이동할 수 있는 길이로, 두세 번째 랑비에결절에서 활동전위를 일으킬 수 있는 충분한 강도가 유지된다. 따라서 결절이 일부 손상되었을 경우에도 신호 전달을 계속할 만큼 도약 전도의 안전 계수는 높다. 다만 수초가 없는 뉴런이라 하더라도 활동전위는 안전 계수가 낮은 일부 지점에서 일찍 사라질 수 있다. 축삭이 가지를 형성하여 두 개로 갈라지는 부분을 예로 들 수 있다.[42]
미엘린 수초가 분해되어 도약 전도 능률이 떨어지고 활동전위 전도 속도가 감소하는 질병으로[u] 가장 잘 알려진 것은 다발성 경화증이 있다. 수초가 분해되어 협동적인 운동 능력이 떨어진다.[43]
케이블 이론[편집]

축삭 내부에서 이온 흐름은 케이블 이론[44] 및 그를 개선한 구획 모델에 의해[45] 양적으로 기술된다. 케이블 이론은 1855년 윌리엄 톰슨이 대서양을 건너는 전보 케이블을 구상하면서 발전하였고,[v] 1946년 호지킨과 러쉬튼(W. A. H. Rushton)이 뉴런에 적용할 수 있음을 보였다.[w] 단순한 케이블 이론에서는 뉴런을 전기적으로 수동적인, 완전한 실린더형 전송 케이블로 간주하며 다음과 같은 편미분방정식으로 기술된다.[44]
V(x, t)는 어떤 시점 t와 뉴런 길이 방향의 어떤 위치 x에서 막 안팎의 전압이고, λ와 τ는 자극에 반응하여 전압이 감쇠하는 특징적인 길이와 시간 크기를 나타낸다. 시간과 길이는 단위 길이당 저항과 전기 용량에서 결정된다.[46]
산출한 시간과 길이의 크기는 수초가 없는 신경 섬유의 경우에 전도 속도가 지름에 의존하는 정도를 이해하는데 쓰인다. 예를 들어, 시간 크기인 τ는 막 저항 rm과 전기 용량 cm 모두에 의해 증가한다. 용량이 증가하면 주어진 막관통 전압을 형성하기 위하여 더 많은 전하가 전이되어야 한다(전기 용량, Q=CV). 저항이 증가하면 단위 시간당 더 적은 전하가 전이되어 느리게 평형을 이룬다. 유사한 방식으로, 단위 길이당 내부 저항 ri가 어떤 축삭에서 작다면(지름이 커서 등), 공간적 감쇠 길이 λ는 더 길어지고 활동전위의 전도 속도는 증가한다. 막관통 저항 rm이 증가하면 막을 통해 유출되는 평균 흐름이 감소하고 마찬가지로 λ가 길어져 전도 속도가 증가한다.
종말[편집]
화학적 시냅스[편집]
일반적으로 시냅스 단추(synaptic knob)에 활동전위가 닿으면 시냅스 틈으로 신경전달물질을 방출한다.[x] 한 축삭의 축삭 말단에는 대부분 동일한 신경전달물질이 들어있다. 신경전달물질은 시냅스후 뉴런의 이온 채널을 여는 작은 분자이다. 활동전위가 도착하면 시냅스전 뉴런의 전압 민감성 칼슘 채널이 열린다. 칼슘이 세포 내로 유입되면 신경전달물질이 든 소포가 세포의 표면으로 이동하여 시냅스 틈으로 내용물을 방출한다.[y] 신경독소인 테타노스파스민(tetanospasmin)과 보툴리눔 독소는 신경전달물질 방출 과정을 억제하여 각각 파상풍과 보툴리누스 중독을 일으킨다.[z]
전기적 시냅스[편집]
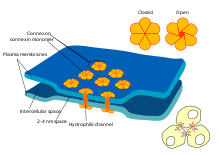
전기적 시냅스에는 신경전달물질을 분배하고 시냅스 전후 세포를 한데 연결하는 분자인 코넥손(connexon)이 있다.[aa] 활동전위가 전기적 시냅스에 닿으면 시냅스전 세포로 들어온 이온은 코넥손을 통하여 두 세포막 장벽을 가로질러 시냅스후 세포로 들어간다.[ab] 시냅스전 활동전위의 이온 흐름은 직접적으로 시냅스후 세포를 자극한다. 전기적 시냅스는 신경전달물질이 시냅스 틈을 가로질러 확산되는 과정을 거치지 않기 때문에 신호 전달이 더 빠르다. 도망 반사, 척추동물의 망막, 심장 등 빠른 반응과 시간적 동기화가 중요한 연결에는 전기적 시냅스가 쓰인다.
신경근육 이음[편집]
신경근육 이음부는 특수한 화학적 시냅스로, 운동뉴런의 축삭이 근섬유에서 끝난다.[ac] 신경근육 이음에서 방출되는 신경전달물질은 아세틸콜린으로, 근섬유 막(근육속막, sarcolemma)에 있는 막 통합 단백질인 아세틸콜린 수용체에 결합한다.[ad] 아세틸콜린은 계속 결합 상태를 유지하지 않고 분리되어 시냅스에 있는 효소 아세틸콜린에스터레이스에 의해 가수분해된다. 아세틸콜린에스터레이스는 근육에 자극을 빠르게 감소시켜 근육이 수축하는 정도와 시간을 섬세하게 조절한다. 신경 작용제 사린과 타분,[ae] 살충제 다이아지논(diazinon)과 말라티온(malathion)은[af] 아세틸콜린에스터레이스를 불활성화하여 이러한 통제를 막는 독소이다.
기타 세포 유형[편집]
심장 활동전위[편집]
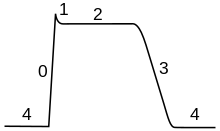
심장 활동전위는 신경 활동전위와 다르다. 심장 활동전위에는 막 전압이 높게 수백 ms 동안 유지되는 구간(plateau)이 있고 칼륨 흐름에 의해 재분극이 되는 일반적인 시기가 뒤따른다.[ag] 전압 유지기는 나트륨 채널이 차단형으로 전환된 후에도 느린 칼슘 채널이 열려있어 막 전위가 칼슘 평형 전위 근처에서 지속되기 때문에 발생한다.
심장 활동전위는 심장이 정확하게 수축하는데 중요한 기능을 한다.[ag] 굴심방 결절에 있는 심장 세포는 박동조율기 전위를 만들어 심장을 동기화한다. 박동조율기 세포의 활동전위는 일반적으로 심방과 심실 사이의 유일한 전도 경로인 방실결절로 전파된다. 방실결절에서 출발한 활동전위는 히스속을 거쳐 푸르키네 섬유[note 2](Purkinje cell, 심장전도근육세포)로 전달된다. 선천적인 변이나 외상으로 심장 활동전위에 이상이 생기면 부정맥 등 질환으로 이어진다.[ag] 퀴니딘, 리도카인, 베타 차단제, 베라파밀 등 항부정맥 약물은 심장 활동전위에 작용한다.[ah]
근육 활동전위[편집]
정상적인 골격근 세포에서 활동전위는 신경의 활동전위와 유사하다.[47] 활동전위는 세포막(근세포막, sarcolemma)이 탈분극하면서 생성되어 전압 민감성 나트륨 채널을 연다. 나트륨 채널이 차단형으로 전환되면 막은 세포 밖으로 유출되는 칼륨 이온에 의해서 재분극된다. 휴지 전위는 약 -90 mV로, 일반적인 뉴런보다 더 낮다. 근육 활동전위는 2 - 4 ms간 지속되고 절대적 불응기는 1 - 3 ms이며, 근육 내 전도 속도는 5 m/s 정도이다. 활동전위는 칼슘 이온을 방출하여 트로포마이오신을 이동시키고 근육이 수축하도록 한다. 신경근육 이음부에 뉴런의 활동전위가 도달하면 근육 활동전위가 발생한다. 신경근육 이음부는 흔히 신경독소의 표적이 된다.[ae]
식물 활동전위[편집]
식물과 진균류[ai] 세포 중에도 전기적으로 흥분하는 세포가 있다. 식물세포가 동물세포와 근본적으로 다른 점은 양전하를 띠는 나트륨 이온을 흡수하는 것이 아니라 염소 이온을 방출하여 탈분극을 일으킨다는 것이다.[aj][ak][al] 염소 이온이 방출된 이후에는 동물의 활동전위와 마찬가지로 양전하를 띠는 칼륨 이온이 방출된다. 종합하면, 동물의 활동전위는 들어오는 나트륨과 나가는 칼륨이 서로를 삼투적으로 상쇄하여 중립적(neutral)이지만, 식물의 활동전위는 염(KCl)이 삼투적으로 손실되는 현상을 가리킨다. 식물세포에서 일어나는 전기와 삼투 관계의 상호작용은[am] 염분 농도가 변화하는 환경에서 식물과 동물의 공통 단세포 조상에서 일어났던 전기적 흥분의 삼투적 기능을 나타낸다. 현재의 빠른 신호 전달은 비교적 최근에 후생동물 세포가 좀 더 안정적인 삼투 환경에서 얻은 것으로 간주한다.[48] 미모사(mimosa pudica) 같은 특정 관다발식물에서 활동전위가 하는 신호 기능은 후생동물의 흥분성 세포와는 독립적으로 진화하였을 것이다.
분류와 진화적 이점[편집]
식물, 곤충 같은 무척추동물, 파충류와 포유류 등 척추동물을 포함하여 다세포생물에 널리 활동전위가 존재한다.[an] 해면동물은 다세포 진핵생물 중 활동전위를 전달하지 않는 주요 문에 속한다. 다만 전기적 형태의 신호를 갖추고 있다는 연구도 있다.[ao] 활동전위의 크기 및 지속 시간과 마찬가지로 휴지전위는 진화를 거치면서 크게 변화하지 않았다. 전도 속도는 반면에 축삭 지름과 미엘린 수초 형성을 통하여 크게 증가하였다.
| 동물 | 세포 유형 | 휴지전위 (mV) | AP 증가 정도 (mV) | AP 지속 시간 (ms) | 전도 속도 (m/s) |
|---|---|---|---|---|---|
| 오징어 (Loligo) | 거대 축삭(giant axon) | −60 | 120 | 0.75 | 35 |
| 지렁이 (Lumbricus) | 중간 거대 섬유(median giant fiber) | −70 | 100 | 1.0 | 30 |
| 바퀴벌레 (Periplaneta) | 거대 섬유(giant fiber) | −70 | 80–104 | 0.4 | 10 |
| 개구리 (Rana) | 좌골 신경 축삭 | −60에서 −80 | 110–130 | 1.0 | 7–30 |
| 고양이 (Felis) | 척수 운동뉴런 | −55에서 −80 | 80–110 | 1–1.5 | 30–120 |
활동전위가 진화를 통해 보존된 것으로 미루어 보아 활동전위에는 진화 상의 이점이 있을 것이다. 활동전위는 빠르고, 생물체 내에서 먼 거리에 걸쳐 신호를 전달하는 기능을 한다. 전도 속도는 음속의 삼 분의 일인 110 m/s를 초과하는 경우도 있다. 혈류를 흐르는 호르몬 분자는 큰 동맥에서 대략 8 m/s의 속도로 움직이며, 심장 수축 등 기계적 요소와 밀접한 관련이 있다. 활동전위의 두 번째 이점은 활동전위가 생성되는 방법이다. 활동전위는 실무율 특성을 가진 신호이기 때문에 거리에 따라 신호 강도가 감소하지 않고, 디지털 전자공학과 유사한 이점을 지닌다. 가지돌기에서 온 다양한 신호가 축삭 언덕에서 통합되어 역치를 넘어 복잡한 활동전위를 생성하는 것은 연산(computation)의 또 다른 형태로, 생물학적 중추 패턴 발생기를 형성하고 인공적으로는 신경망에서 모방된다.
실험 방법[편집]

활동전위 연구에는 새로운 실험적 기술이 필요했다. 1955년 이전에 초기 연구는 세 가지 목표, 즉 단일 뉴런이나 축삭의 신호를 분리하는 것, 빠르고 민감한 전자 장치를 개발하는 것, 단일 세포 내부의 전압을 기록할 수 있을 정도로 전극을 작게 줄이는 것에 초점을 맞추었다.
첫 번째 목표는 오징어의 한 속인 Loligo의 뉴런에 있는 거대 축삭을 연구하여 해결하였다.[ap] 거대 축삭은 지름이 대략 1 mm로 일반적인 축삭 지름의 100배에 이르고, 맨눈으로 볼 수 있어 추출하고 조작하기 쉽다.[g][aq] 그러나 Loligo의 축삭은 모든 흥분성 세포를 대표할 만한 세포는 아니고, 활동전위와 관련된 수많은 다른 장치가 연구되었다.
두 번째 문제는 결정적으로 전압 클램프가 개발되어 해결되었다.[ar] 전압 클램프는 활동전위를 일으키는 이온 흐름을 분리하여 연구할 수 있게 하였고, 전기적인 잡음을 만드는 주요 원인인 막의 전기 용량 C와 관련된 전류 IC를 제거하였다.[50] 전류는 C에 막관통 전위 Vm 변화율을 곱한 것과 같으므로 막 사이에 흐르는 전류와 관계없이 Vm을 고정(변화율이 0)시킨 회로를 고안한 것이다. 따라서 Vm을 고정값에 유지하기 위해 필요한 전류가 막 안팎으로 흐르는 전류를 그대로 반영한다. 패러데이 새장이나 고입력 임피던스(input impedance)를 가진 전기 장치를 포함한 기타 전자공학적 진전으로 측정 자체로 인하여 전압에 미치는 영향을 없앴다.[51]
세 번째 문제, 즉 단일 축삭 내의 전압을 기록하면서 교란을 일으키지 않을 정도로 작은 전극을 얻는 문제는 1949년 유리 마이크로피펫 전극을 발명하여 해결하였다.[as] 연구자들은 재빨리 이 전극을 사용하였으며,[at][au] 전극을 개선하여 끝이 100 Å(10 nm)에 불과한, 마찬가지로 고입력 임피던스를 주는 전극을 생산하였다.[52] 활동전위는 작은 금속 전극을 뉴런 바로 옆에 두거나, EOSFET을 포함한 뉴로칩(neurochip)을 이용하여, 전압 혹은 Ca2+에 민감한 염료를 통하여 광학적으로 기록할 수도 있다.[av]

유리 마이크로피펫 전극은 이온 채널 여러 개를 지나는 전류의 합을 측정하지만, 1970년대에 에르빈 네어와 베르트 자크만이 패치 클램프를 고안하면서 단일 이온 채널의 전기적인 특성을 연구할 수 있게 되었다. 네어와 자크만은 이 공로로 1991년 노벨 생리학·의학상을 수상한다.[lower-greek 3] 패치 클램프 방법을 통하여 이온 채널이 열린형, 닫힌형, 차단형으로 구별되는 전도 상태를 거친다는 것이 확인되었다.
광학 영상 기술은 활동전위를 동시에 여러 군데에서나 초공간적인 해상도로 기록하기 위하여 최근에 발전한 기술이다. 심근세포 막의 아주 작은 일부에서 전압 민감성 염료(voltage-sensitive dye)를 이용하여 광학적으로 활동전위를 기록한 바 있다.[aw]
신경독소[편집]

신경독소는 활동전위를 차단하는 물질로, 자연계에 존재하기도 하고 합성되기도 한다. 복어의 테트로도톡신과 와편모충류에 속하는 적조 Gonyaulax속의 색시톡신은 전압 민감성 나트륨 채널을 저해하여 활동전위를 차단한다.[ax] 아프리카산 독사 맘바의 덴드로톡신도 전압 민감성 칼륨 채널을 차단한다. 이온 채널의 저해제는 특정한 이온 채널을 차단하여 다른 채널의 역할을 따로 연구하는 데에 쓰인다. 이온 채널을 친화성 크로마토그래피로 분리 정제할 때에도 유용하다. 저해제는 효과적인 신경독소로 작용할 수도 있어 화학 무기로 쓰일 가능성이 있다. 곤충의 이온 채널을 표적으로 삼는 신경독소는 효율적인 살충제이다. 합성 퍼메트린(permethrin)은 활동전위에 관여하는 나트륨 채널의 활성을 연장시킨다. 곤충의 이온 채널은 사람의 것과 충분히 다르기 때문에 사람에게 부작용은 거의 없다. 다른 신경독소 중에는 시냅스, 특히 신경근 접합부에서 활동전위가 전달되는 것을 방해하는 것도 있다.
역사[편집]
동물 신경계의 전기 활성은 1791년에서 1797년 사이 루이지 갈바니가 개구리를 해부하면서 처음으로 관찰하였다.[ay] 갈바니의 관찰 결과는 알레산드로 볼타를 자극하였고, 그는 최초의 전지인 볼타 전지를 개발하였다. 볼타는 전기뱀장어 같은 동물의 전기와 직류 전압에서 생리학적 반응을 연구하였다.[az]
19세기 과학자들은 신경 다발에서 일어나는 전기 신호 전파를 연구하고 신경 조직이 서로 연결된 관으로 된 망(reticulum)이 아니라 세포로 이루어져 있다는 것을 증명하였다.[53] 카를로 마테우치(이탈리아어: Carlo Matteucci)가 갈바니의 뒤를 이어 세포막 안팎으로 전압이 형성되어 있으며 직류 전류를 생산할 수 있다는 것을 증명하였다. 마테우치의 작업은 독일의 생리학자인 에밀 뒤 부아레몽(Emil du Bois-Reymond)에게 영감을 주었고, 그는 1848년 활동전위를 발견한다. 활동전위의 전도 속도는 1850년 뒤 부아레몽의 친구인 헤르만 폰 헬름홀츠가 처음 측정하였다. 신경조직이 개개의 세포로 형성되어 있다는 것을 증명하기 위하여 스페인 의사 산티아고 라몬 이 카할은 카밀로 골지가 발명한 염색법을 이용하여 뉴런의 수많은 형태를 밝혔다. 골지와 라몬 이 카할은 그 공로로 1906년 노벨 생리학·의학상을 수상하였다.[lower-greek 4] 그들의 연구는 19세기 신경해부학 분야의 오랜 논쟁을 종식시켰다. 특히 골지는 신경계가 신경망으로 구성되어 있다고 주장하였다.
20세기는 전기생리학의 황금기였다. 1902년과 1912년에 율리우스 베른슈타인은 축삭 막에서 이온의 투과성이 변한 결과 활동전위가 생긴다는 가설을 발전시켰다.[ba][54] 켄 콜(Ken Cole)과 하워드 커티스(Howard Curtis)가 막 전도율이 활동전위 동안 증가한다는 것을 증명하면서 베른슈타인의 가설은 확실해졌다.[bb] 1907년에 루이 라피크(프랑스어: Louis Lapicque)는 활동전위가 역치를 넘어서면서 발생한다고 주장하였고,[bc] 이후 이온 전도율이 역동적으로 변화한 결과임이 증명된다. 1949년에 앨런 호지킨과 베르나르트 카츠(독일어: Bernard Katz)는 축삭 막이 서로 다른 이온에 대해 투과성이 다를 것을 고려하여 베른슈타인의 가설을 발전시켰다. 특히 호지킨과 카츠는 활동전위에서 나트륨 투과성이 하는 중요한 역할을 증명하였다.[bd] 그들은 활동전위를 일으키는 신경 막 안팎의 실제 전기적 변화를 최초로 기록하였다.[lower-greek 5] 1952년 출판된 논문 5개에서 호지킨과 카츠, 그리고 앤드루 헉슬리는 전압 클램프 기술을 도입한다. 그들은 축삭 막의 나트륨 및 칼륨 이온 투과성이 전압과 시간에 의존하는 정도를 측정하였고, 활동전위를 양적으로 재구성할 수 있었다.[g] 호지킨과 헉슬리는 열린형, 닫힌형, 차단형 등 세 형태로 존재할 수 있는 개개의 이온 채널과 연관된 수학적 모델을 고안하였다. 이 가설은 1970년대 중반과 80년대에 걸쳐 에르빈 네어와 베르트 자크만이 개별 이온 채널에서 전도율을 측정하는 패치 클램프 기술을 고안하면서 검증되었다.[be] 21세기에 들어서 원자 수준 해상도의 결정 구조[bf]와 형광을 이용한 거리 측정,[bg] 동결전자현미경[bh] 연구를 통하여 특정한 채널이 각기 다른 종류의 이온에 갖는 선택성과 전도 상태에 대한 구조적 기반에 대하여[bi] 이해하기 시작한다.
율리우스 베른슈타인은 막 안팎의 휴지전위에 네른스트 식을 처음으로 적용하였고, 데이비드 E. 골드만이 1943년에 골드만 방정식을 통하여 일반화하였다.[f] 나트륨-칼륨 펌프가 1957년 발견되었고[bj][lower-greek 6] 펌프의 특성이 점차 밝혀졌으며,[bk][bl][bm] 마침내 X선 결정법으로 원자 분해능 구조를 결정하였다.[bn] 관련된 이온 펌프의 결정 구조 또한 밝혀져 분자 기구가 어떻게 기능하는지에 대한 시야를 넓혀주고 있다.[bo]
양적 모델[편집]

활동전위를 이해하는 데에는 수학적 및 계산적 모델이 필수적으로, 실험적 자료에 대하여 검증할 수 있는 예측값을 제시하여 이론에 대한 정밀한 측정을 가능케 한다. 가장 정확하고 중요한 위치를 차지하고 있는 모델은 호지킨-헉슬리 모델로, 활동전위를 네 개의 상미분 방정식(ordinary differential equation, ODE)으로 설명한다.[g] 호지킨-헉슬리 모델이 자연계에 실재하는 신경계 막을 단순화한 것일 수 있지만, 그 복잡성에서 더욱 단순화된, 두 개의 상미분 방정식으로 기술되는 모델인[55][bp] 모리스-레카 모델(Morris-Lecar model)[bq]과 피츠휴-나구모 모델(FitzHugh-Nagumo model)[br]이 탄생하였다. 호지킨-헉슬리 모델과 피츠휴-나구모 모델 및 그와 관련된 본회퍼-반데르 폴 모델[bs] 등의 특성은 수학,[56][bt] 계산,[57] 그리고 전자공학 분야에서 널리 연구 대상이 되었다.[bu] 현대의 연구는 크고 통합적인 계에 집중한다. 활동전위에 대한 모델을 신경계의 다른 부분, 즉 가지돌기와 시냅스에 대한 모델과 결합하여 신경 계산과[58] 도망 반사 및 중추 패턴 발생기가 통제하는 기타 단순 반사를 연구한다.[59][bv]
각주 및 참고 문헌[편집]
내용주[편집]
참조주[편집]
- ↑ 가 나 다 라 마 바 사 아 Bullock, Orkand & Grinnell 1977, 150–151쪽.
- ↑ 가 나 다 라 마 Junge 1981, 89–90쪽.
- ↑ 가 나 Schmidt-Nielsen 1997, 484쪽.
- ↑ 가 나 다 Purves et al. 2008, pp. 48–49; Bullock, Orkand & Grinnell 1977, p. 141; Schmidt-Nielsen 1997, p. 483; Junge 1981, p. 89.
- ↑ Stevens 1966, 127쪽.
- ↑ Schmidt-Nielsen, p. 484.
- ↑ Bullock, Orkand & Grinnell 1977, 11쪽.
- ↑ Silverthorn 2010, 253쪽.
- ↑ 가 나 다 Purves et al. 2008, pp. 49–50; Bullock, Orkand & Grinnell 1977, pp. 140–141; Schmidt-Nielsen 1997, pp. 480–481.
- ↑ 가 나 다 라 Schmidt-Nielsen 1997, 483–484쪽.
- ↑ Bullock, Orkand & Grinnell 1977, pp. 177–240; Schmidt-Nielsen 1997, pp. 490–499; Stevens 1966, p. 47-68.
- ↑ Bullock, Orkand & Grinnell 1977, pp. 178–180; Schmidt-Nielsen 1997, pp. 490–491.
- ↑ Silverthorn DU (2011년 3월 1일). 〈8장 뉴런: 세포와 네트워크의 특성〉. 고영규 외 역. 《인체생리학》 5판. 라이프사이언스. ISBN 978-89-6154-101-5.
- ↑ Purves 등. 2001.
- ↑ Purves 등. 2008, 26–28쪽.
- ↑ Schmidt-Nielsen 1997, pp. 535–580; Bullock, Orkand & Grinnell 1977, pp. 49–56, 76–93, 247–255; Stevens 1966, pp. 69–79.
- ↑ Bullock, Orkand & Grinnell 1977, pp. 53; Bullock, Orkand & Grinnell 1977, pp. 122–124.
- ↑ Junge 1981, 115–132쪽.
- ↑ 가 나 Bullock, Orkand & Grinnell 1977, 152–153쪽.
- ↑ Bullock, Orkand & Grinnell 1977, 444–445쪽.
- ↑ Purves 등. 2008, 38쪽.
- ↑ Stevens 1966, 127–128쪽.
- ↑ Purves 등. 2008, 61-65쪽.
- ↑ Purves et al. 2008, pp. 64–74; Bullock, Orkand & Grinnell 1977, pp. 149–150; Junge 1981, pp. 84–85; Stevens 1966, pp. 152–158.
- ↑ 가 나 다 Purves et al. 2008, p. 47; Purves et al. 2008, p. 65; Bullock, Orkand & Grinnell 1977, pp. 147–148; Stevens 1966, p. 128.
- ↑ Goldin, AL in Waxman 2007, Neuronal Channels and Receptors, pp. 43-58.
- ↑ Stevens 1966, 49쪽.
- ↑ Purves et al. 2008, p. 34; Bullock, Orkand & Grinnell 1977, p. 134; Schmidt-Nielsen 1997, pp. 478–480.
- ↑ 가 나 다 라 Purves 등. 2008, 49쪽.
- ↑ 가 나 다 라 Stevens 1966, 19–20쪽.
- ↑ 가 나 다 Bullock, Orkand & Grinnell 1977, p. 151; Junge 1981, pp. 4–5.
- ↑ 가 나 Bullock, Orkand & Grinnell 1977, 152쪽.
- ↑ Bullock, Orkand & Grinnell 1977, pp. 147–149; Stevens 1966, pp. 126–127.
- ↑ Purves 등. 2008, 37쪽.
- ↑ 가 나 Purves 등. 2008, 56쪽.
- ↑ Bullock, Orkland & Grinnell 1977, 160–164쪽.
- ↑ Stevens 1966, 21–23쪽.
- ↑ Bullock, Orkland & Grinnell 1977, 161–164쪽.
- ↑ Bullock, Orkland & Grinnell 1977, 509쪽.
- ↑ Tasaki, I in Field 1959, 75–121쪽
- ↑ Schmidt-Nielsen 1997, Figure 12.13.
- ↑ Bullock, Orkland & Grinnell 1977, 163쪽.
- ↑ Waxman, SG in Waxman 2007, Multiple Sclerosis as a Neurodegenerative Disease, pp. 333-346.
- ↑ 가 나 Rall, W in Koch & Segev 1989, Cable Theory for Dendritic Neurons, p. 9-62.
- ↑ Segev, I; Fleshman, JW; Burke, RE in Koch & Segev 1989, Compartmental Models of Complex Neurons, pp. 63-96.
- ↑ Purves 등. 2008, 52–53쪽.
- ↑ Ganong 1991, 59–60쪽.
- ↑ Gradmann, D; Mummert, H in Spanswick, Lucas & Dainty 1980, Plant action potentials, pp. 333-344.
- ↑ Bullock 1965.
- ↑ Junge 1981, 63–82쪽.
- ↑ Kettenmann & Grantyn 1992.
- ↑ Snell, FM in Lavallee, Schanne & Hebert 1969, Some Electrical Properties of Fine-Tipped Pipette Microelectrodes.
- ↑ Brazier 1961; McHenry & Garrison 1969; Worden, Swazey & Adelman 1975.
- ↑ Bernstein 1912.
- ↑ Hoppensteadt 1986.
- ↑ Sato, S; Fukai, H; Nomura, T; Doi, S in Reeke 등. 2005, Bifurcation Analysis of the Hodgkin-Huxley Equations, pp. 459-478.
* FitzHugh, R in Schwann 1969, Mathematical models of axcitation and propagation in nerve, pp. 12-16.
* Guckenheimer & Holmes 1986, 12–16쪽 - ↑ Nelson, ME; Rinzel, J in Bower & Beeman 1995, The Hodgkin-Huxley Model, pp. 29-49.
* Rinzel, J & Ermentrout, GB; in Koch & Segev 1989, Analysis of Neural Excitability and Oscillations, pp. 135-169. - ↑ McCulloch 1988, pp. 19–39, 46–66, 72–141; Anderson & Rosenfeld 1988, pp. 15–41.
- ↑ Getting, PA in Koch & Segev 1989, Reconstruction of Small Neural Networks, pp. 171-194.
서적[편집]
- Anderson JA, Rosenfeld E ed. (1988). 《Neurocomputing: Foundations of Research》. Cambridge, Mass.: The MIT Press. ISBN 978-0-262-01097-9. LCCN 87003022. OCLC 15860311.
- Bernstein, J (1912). 《Elektrobiologie, die Lehre von den elektrischen Vorgängen im Organismus auf moderner Grundlage dargestellt》 [Electric Biology, the study of the electrical processes in the organism represented on a modern basis]. Braunschweig: Vieweg und Sohn. LCCN 12027986. OCLC 11358569.
- Bower JM, Beeman D (1995). 《The Book of GENESIS: Exploring Realistic Neural Models with the GEneral NEural SImulation System》. Santa Clara, Calif.: TELOS. ISBN 978-0-387-94019-9. LCCN 94017624. OCLC 30518469.
- Brazier, MAB (1961). 《A History of the Electrical Activity of the Brain》. London: Pitman. LCCN 62001407. OCLC 556863.
- Bullock TH, Horridge GA (1965). 《Structure and Function in the Nervous Systems of Invertebrates》. A series of books in biology. San Francisco: W. H. Freeman. LCCN 65007965. OCLC 558128.
- Bullock TH, Orkand R, Grinnell A (1977). 《Introduction to Nervous Systems》. A series of books in biology. San Francisco: W. H. Freeman. ISBN 978-0-7167-0030-2. LCCN 76003735. OCLC 2048177.
- Field J ed. 《Handbook of Physiology: a Critical, Comprehensive Presentation of Physiological Knowledge and Concepts: Section 1: Neurophysiology》 1. Washington, DC: American Physiological Society. LCCN 60004587. OCLC 830755894.
- Ganong, WF (1991). 《Review of Medical Physiology》 15판. Norwalk, Conn.: Appleton and Lange. ISBN 978-0-8385-8418-7. ISSN 0892-1253. LCCN 87642343. OCLC 23761261.
- Guckenheimer J, Holmes P (1986). 《Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields》. Applied Mathematical Sciences 42 2판. New York: Springer Verlag. ISBN 978-0-387-90819-9. OCLC 751129941.
- Hoppensteadt, FC (1986). 《An Introduction to the Mathematics of Neurons》. Cambridge studies in mathematical biology 6. Cambridge: Cambridge University Press. ISBN 978-0-521-31574-6. LCCN 85011013. OCLC 12052275.
- Junge, D (1981). 《Nerve and Muscle Excitation》 2판. Sunderland, Mass.: Sinauer Associates. ISBN 978-0-87893-410-2. LCCN 80018158. OCLC 6486925.
- Kettenmann H, Grantyn R ed. (1992). 《Practical Electrophysiological Methods: A Guide for In Vitro Studies in Vertebrate Neurobiology》. New York: Wiley. ISBN 978-0-471-56200-9. LCCN 92000179. OCLC 25204689.
- Keynes RD, Aidley DJ (1991). 《Nerve and Muscle》 2판. Cambridge: Cambridge University Press. ISBN 978-0-521-41042-7. LCCN 90015167. OCLC 25204483.
- Koch C, Segev I ed. (1989). 《Methods in Neuronal Modeling: From Synapses to Networks》. Cambridge, Mass.: The MIT Press. ISBN 978-0-262-11133-1. LCCN 88008279. OCLC 18384545.
- Lavallée M, Schanne OF, Hébert NC ed. (1969). 《Glass Microelectrodes》. New York: Wiley. ISBN 978-0-471-51885-3. LCCN 68009252. OCLC 686.
- McCulloch, WS (1988). 《Embodiments of Mind》. Cambridge, Mass.: The MIT Press. ISBN 978-0-262-63114-3. LCCN 88002987. OCLC 237280.
- McHenry LC, Garrison FH (1969). 《Garrison's History of Neurology》. Springfield, Ill.: Charles C. Thomas. OCLC 429733931.
- Silverthorn, DU (2010). 《Human Physiology: An Integrated Approach》 5판. San Francisco: Pearson. ISBN 978-0-321-55980-7. LCCN 2008050369. OCLC 268788623.
- Spanswick RM, Lucas WJ, Dainty J ed. (1980). 《Plant Membrane Transport: Current Conceptual Issues》. Developments in Plant Biology 4. Amsterdam: Elsevier Biomedical Press. ISBN 978-0-444-80192-0. LCCN 79025719. OCLC 5799924.
- Purves D, Augustine GJ, Fitzpatrick D, Hall WC, Lamantia A-S, McNamara JO, Williams SM (2001). 〈Release of Transmitters from Synaptic Vesicles〉. 《Neuroscience》 2판. Sunderland, MA: Sinauer Associates. ISBN 978-0-87893-742-4. LCCN 00059496. OCLC 806472664.
- Purves D, Augustine GJ, Fitzpatrick D, Hall WC, Lamantia A-S, McNamara JO, White LE (2008). 《Neuroscience》 4판. Sunderland, MA: Sinauer Associates. ISBN 978-0-87893-697-7. LCCN 2007024950. OCLC 144771764.
- Reeke GN, Poznanski RR, Sporns O, Rosenberg JR, Lindsay KA (2005). 《Modeling in the Neurosciences: from Biological Systems to Neuromimetic Robotics》. Boca Raton, Fla.: Taylor & Francis. ISBN 978-0-415-32868-5. LCCN 2005298022. OCLC 489024131.
- Schmidt-Nielsen, K (1997). 《Animal Physiology: Adaptation and Environment》 5판. Cambridge: Cambridge University Press. ISBN 978-0-521-57098-5. LCCN 96039295. OCLC 35744403.
- Schwann HP ed. (1969). 《Biological Engineering》. Inter-University Electronics Series 9. New York: McGraw-Hill. ISBN 978-0-07-055734-5. LCCN 68027513. OCLC 51993.
- Stevens, CF (1966). 《Neurophysiology: A Primer》. New York: John Wiley and Sons. LCCN 66015872. OCLC 1175605.
- Waxman SG ed. (2007). 《Molecular Neurology》. Burlington, Mass.: Elsevier Academic Press. ISBN 978-0-12-369509-3. LCCN 2008357317. OCLC 154760295.
- Worden FG, Swazey JP, Adelman G ed. (1975). 《The Neurosciences, Paths of Discovery》. Cambridge, Mass.: The MIT Press. ISBN 978-0-262-23072-8. LCCN 75016379. OCLC 1500233.
저널[편집]
- ↑ Golding NL, Kath WL, Spruston N (December 2001). “Dichotomy of action-potential backpropagation in CA1 pyramidal neuron dendrites”. 《J. Neurophysiol.》 86 (6): 2998–3010. PMID 11731556.
- ↑ Sasaki, T., Matsuki, N., Ikegaya, Y. 2011 Action-potential modulation during axonal conduction Science 331 (6017), pp. 599-601
- ↑ Aur D., Connolly C.I., Jog M.S., (2005) Computing spike directivity with tetrodes, Journal of Neuroscience Methods, 149 (1), pp. 57-63
- ↑ Aur D., Jog, MS., 2010 Neuroelectrodynamics: Understanding the brain language, IOS Press, 2010. http://dx.doi.org/10.3233/978-1-60750-473-3-i
- ↑ Noble D (1960). “Cardiac action and pacemaker potentials based on the Hodgkin-Huxley equations”. 《Nature》 188 (4749): 495–497. Bibcode:1960Natur.188..495N. doi:10.1038/188495b0. PMID 13729365.
- ↑ 가 나 Goldman DE (1943). “Potential, impedance and rectification in membranes”. 《J. Gen. Physiol.》 27 (1): 37–60. doi:10.1085/jgp.27.1.37. PMC 2142582. PMID 19873371.
- ↑ 가 나 다 라 마 Hodgkin AL, Huxley AF, Katz B (1952). “Measurements of current-voltage relations in the membrane of the giant axon of Loligo”. 《Journal of Physiology》 116 (4): 424–448. PMC 1392213. PMID 14946713.
* Hodgkin AL, Huxley AF (1952). “Currents carried by sodium and potassium ions through the membrane of the giant axon of Loligo”. 《Journal of Physiology》 116 (4): 449–472. PMC 1392213. PMID 14946713.
* Hodgkin AL, Huxley AF (1952). “The components of membrane conductance in the giant axon of Loligo”. 《J Physiol》 116 (4): 473–496. PMC 1392209. PMID 14946714.
* Hodgkin AL, Huxley AF (1952). “The dual effect of membrane potential on sodium conductance in the giant axon of Loligo”. 《J Physiol》 116 (4): 497–506. PMC 1392212. PMID 14946715.
* Hodgkin AL, Huxley AF (1952). “A quantitative description of membrane current and its application to conduction and excitation in nerve”. 《J Physiol》 117 (4): 500–544. PMC 1392413. PMID 12991237. - ↑ Naundorf B, Wolf F, Volgushev M (April 2006). “Unique features of action potential initiation in cortical neurons” (Letter). 《Nature》 440 (7087): 1060–1063. Bibcode:2006Natur.440.1060N. doi:10.1038/nature04610. PMID 16625198. 2008년 3월 27일에 확인함.
- ↑ Hodgkin AL (1937). “Evidence for electrical transmission in nerve, Part I”. 《Journal of Physiology》 90 (2): 183–210. PMC 1395060. PMID 16994885.
* Hodgkin AL (1937). “Evidence for electrical transmission in nerve, Part II”. 《Journal of Physiology》 90 (2): 211–32. PMC 1395062. PMID 16994886. - ↑ Zalc B (2006). “The acquisition of myelin: a success story”. 《Novartis Found. Symp.》. Novartis Foundation Symposia 276: 15–21; discussion 21–5, 54–7, 275–81. doi:10.1002/9780470032244.ch3. ISBN 978-0-470-03224-4. PMID 16805421.
- ↑ S. Poliak & E. Peles (2006). “The local differentiation of myelinated axons at nodes of Ranvier”. 《Nature Reviews Neuroscience》 12 (4): 968–80. doi:10.1038/nrn1253. PMID 14682359.
- ↑ Simons M, Trotter J (October 2007). “Wrapping it up: the cell biology of myelination”. 《Curr. Opin. Neurobiol.》 17 (5): 533–40. doi:10.1016/j.conb.2007.08.003. PMID 17923405.
- ↑ Xu K, Terakawa S (1999년 8월 1일). “Fenestration nodes and the wide submyelinic space form the basis for the unusually fast impulse conduction of shrimp myelinated axons”. 《J. Exp. Biol.》 202 (Pt 15): 1979–89. PMID 10395528. 2020년 3월 24일에 원본 문서에서 보존된 문서. 2014년 11월 17일에 확인함.
- ↑ 가 나 Hursh JB (1939). “Conduction velocity and diameter of nerve fibers”. 《American Journal of Physiology》 127: 131–39.
- ↑ Lillie RS (1925). “Factors affecting transmission and recovery in passive iron nerve model”. 《J. Gen. Physiol.》 7 (4): 473–507. doi:10.1085/jgp.7.4.473. PMC 2140733. PMID 19872151. See also Keynes and Aidley, p. 78.
- ↑ Tasaki I (1939). “Electro-saltatory transmission of nerve impulse and effect of narcosis upon nerve fiber”. 《Amer. J. Physiol.》 127: 211–27.
- ↑ Tasaki I, Takeuchi T (1941). “Der am Ranvierschen Knoten entstehende Aktionsstrom und seine Bedeutung für die Erregungsleitung”. 《Pflüger's Arch. Ges. Physiol.》 244 (6): 696–711. doi:10.1007/BF01755414.
* Tasaki I, Takeuchi T (1942). “Weitere Studien über den Aktionsstrom der markhaltigen Nervenfaser und über die elektrosaltatorische Übertragung des nervenimpulses”. 《Pflüger's Arch. Ges. Physiol.》 245 (5): 764–82. doi:10.1007/BF01755237. - ↑ Huxley A, Stämpfli R (1949). “Evidence for saltatory conduction in peripheral myelinated nerve-fibers”. 《Journal of Physiology》 108: 315–39.
* Huxley A, Stämpfli R (1949). “Direct determination of membrane resting potential and action potential in single myelinated nerve fibers”. 《Journal of Physiology》 112 (3–4): 476–95. PMC 1393015. PMID 14825228. - ↑ Rushton WAH (1951). “A theory of the effects of fibre size in the medullated nerve”. 《Journal of Physiology》 115 (1): 101–22. PMC 1392008. PMID 14889433.
- ↑ 가 나 Hartline DK, Colman DR (2007). “Rapid conduction and the evolution of giant axons and myelinated fibers”. 《Curr. Biol.》 17 (1): R29–R35. doi:10.1016/j.cub.2006.11.042. PMID 17208176.
- ↑ Miller RH, Mi S (2007). “Dissecting demyelination”. 《Nat. Neurosci.》 10 (11): 1351–54. doi:10.1038/nn1995. PMID 17965654.
- ↑ Kelvin WT (1855). “On the theory of the electric telegraph”. 《Proceedings of the Royal Society》 7: 382–99. doi:10.1098/rspl.1854.0093.
- ↑ Hodgkin AL, Rushton WAH (1946). “The electrical constants of a crustacean nerve fibre”. 《Proceedings of the Royal Society B》 133 (873): 444–79. Bibcode:1946RSPSB.133..444H. doi:10.1098/rspb.1946.0024. PMID 20281590.
- ↑ Süudhof TC (2008). “Neurotransmitter release”. 《Handb Exp Pharmacol》. Handbook of Experimental Pharmacology 184 (184): 1–21. doi:10.1007/978-3-540-74805-2_1. ISBN 978-3-540-74804-5. PMID 18064409.
- ↑ Rusakov DA (August 2006). “Ca2+-dependent mechanisms of presynaptic control at central synapses”. 《Neuroscientist》 12 (4): 317–26. doi:10.1177/1073858405284672. PMC 2684670. PMID 16840708.
- ↑ Humeau Y, Doussau F, Grant NJ, Poulain B (May 2000). “How botulinum and tetanus neurotoxins block neurotransmitter release”. 《Biochimie》 82 (5): 427–46. doi:10.1016/S0300-9084(00)00216-9. PMID 10865130.
- ↑ Zoidl G, Dermietzel R (2002). “On the search for the electrical synapse: a glimpse at the future”. 《Cell Tissue Res.》 310 (2): 137–42. doi:10.1007/s00441-002-0632-x. PMID 12397368.
- ↑ Brink PR, Cronin K, Ramanan SV (1996). “Gap junctions in excitable cells”. 《J. Bioenerg. Biomembr.》 28 (4): 351–8. doi:10.1007/BF02110111. PMID 8844332.
- ↑ Hirsch NP (July 2007). “Neuromuscular junction in health and disease”. 《Br J Anaesth》 99 (1): 132–8. doi:10.1093/bja/aem144. PMID 17573397.
- ↑ Hughes BW, Kusner LL, Kaminski HJ (April 2006). “Molecular architecture of the neuromuscular junction”. 《Muscle Nerve》 33 (4): 445–61. doi:10.1002/mus.20440. PMID 16228970.
- ↑ 가 나 Newmark J (2007). “Nerve agents”. 《Neurologist》 13 (1): 20–32. doi:10.1097/01.nrl.0000252923.04894.53. PMID 17215724.
- ↑ Costa LG (2006). “Current issues in organophosphate toxicology”. 《Clin. Chim. Acta》 366 (1–2): 1–13. doi:10.1016/j.cca.2005.10.008. PMID 16337171.
- ↑ 가 나 다 Kléber AG, Rudy Y (April 2004). “Basic mechanisms of cardiac impulse propagation and associated arrhythmias”. 《Physiol. Rev.》 84 (2): 431–88. doi:10.1152/physrev.00025.2003. PMID 15044680.
- ↑ Tamargo J, Caballero R, Delpón E (January 2004). “Pharmacological approaches in the treatment of atrial fibrillation”. 《Curr. Med. Chem.》 11 (1): 13–28. doi:10.2174/0929867043456241. PMID 14754423.
- ↑ Slayman CL, Long WS, Gradmann D (1976). “Action potentials in Neurospora crassa , a mycelial fungus”. 《Biochimica et Biophysica Acta》 426 (4): 737–744. doi:10.1016/0005-2736(76)90138-3. PMID 130926.
- ↑ Mummert H, Gradmann D (1991). “Action potentials in Acetabularia: measurement and simulation of voltage-gated fluxes”. 《Journal of Membrane Biology》 124 (3): 265–273. doi:10.1007/BF01994359. PMID 1664861.
- ↑ Gradmann D (2001). “Models for oscillations in plants”. 《Austr. J. Plant Physiol.》 28: 577–590.
- ↑ Beilby MJ (2007). “Action potentials in charophytes”. 《Int. Rev. Cytol.》. International Review of Cytology 257: 43–82. doi:10.1016/S0074-7696(07)57002-6. ISBN 978-0-12-373701-4. PMID 17280895.
- ↑ Gradmann D, Hoffstadt J (1998). “Electrocoupling of ion transporters in plants: Interaction with internal ion concentrations”. 《Journal of Membrane Biology》 166 (1): 51–59. doi:10.1007/s002329900446. PMID 9784585.
- ↑ Fromm J, Lautner S (2007). “Electrical signals and their physiological significance in plants”. 《Plant Cell Environ.》 30 (3): 249–257. doi:10.1111/j.1365-3040.2006.01614.x. PMID 17263772.
- ↑ Leys SP, Mackie GO, Meech RW (1999년 5월 1일). “Impulse conduction in a sponge”. 《J. Exp. Biol.》 202 (9): 1139–50. PMID 10101111. 2022년 2월 13일에 원본 문서에서 보존된 문서. 2014년 11월 17일에 확인함.
- ↑ Keynes RD (1989). “The role of giant axons in studies of the nerve impulse”. 《BioEssays》 10 (2–3): 90–93. doi:10.1002/bies.950100213. PMID 2541698.
- ↑ Meunier C, Segev I (2002). “Playing the devil's advocate: is the Hodgkin-Huxley model useful?”. 《Trends Neurosci.》 25 (11): 558–63. doi:10.1016/S0166-2236(02)02278-6. PMID 12392930.
- ↑ Cole KS (1949). “Dynamic electrical characteristics of the squid axon membrane”. 《Arch. Sci. Physiol.》 3: 253–8.
- ↑ Ling G, Gerard RW (1949). “The normal membrane potential of frog sartorius fibers”. 《J. Cell. Comp. Physiol.》 34 (3): 383–396. doi:10.1002/jcp.1030340304. PMID 15410483.
- ↑ Nastuk WL, Hodgkin AL (1950). “The electrical activity of single muscle fibers”. 《J. Cell. Comp. Physiol.》 35: 39–73. doi:10.1002/jcp.1030350105.
- ↑ Brock LG, Coombs JS, Eccles JC (1952). “The recording of potentials from motoneurones with an intracellular electrode”. 《J. Physiol. (London)》 117: 431–460.
- ↑ Ross WN, Salzberg BM, Cohen LB, Davila HV (1974). “A large change in dye absorption during the action potential”. 《Biophysical Journal》 14 (12): 983–986. Bibcode:1974BpJ....14..983R. doi:10.1016/S0006-3495(74)85963-1. PMC 1334592. PMID 4429774.
* Grynkiewicz G, Poenie M, Tsien RY (1985). “A new generation of Ca2+ indicators with greatly improved fluorescence properties”. 《J. Biol. Chem.》 260 (6): 3440–3450. PMID 3838314. - ↑ Bu G, Adams H, Berbari EJ, Rubart M (March 2009). “Uniform action potential repolarization within the sarcolemma of in situ ventricular cardiomyocytes”. 《Biophys. J.》 96 (6): 2532–46. Bibcode:2009BpJ....96.2532B. doi:10.1016/j.bpj.2008.12.3896. PMC 2907679. PMID 19289075.
- ↑ Nakamura Y, Nakajima S, Grundfest H (1965). “The effect of tetrodotoxin on electrogenic components of squid giant axons”. 《J. Gen. Physiol.》 48 (6): 985–996. doi:10.1085/jgp.48.6.975.
* Ritchie JM, Rogart RB (1977). “The binding of saxitoxin and tetrodotoxin to excitable tissue”. 《Rev. Physiol. Biochem. Pharmacol.》. Reviews of Physiology, Biochemistry and Pharmacology 79: 1–50. doi:10.1007/BFb0037088. ISBN 0-387-08326-X. PMID 335473.
* Keynes RD, Ritchie JM (1984). “On the binding of labelled saxitoxin to the squid giant axon”. 《Proc. R. Soc. Lond.》 239: 393–434. - ↑ Piccolino M (1997). “Luigi Galvani and animal electricity: two centuries after the foundation of electrophysiology”. 《Trends in Neuroscience》 20 (10): 443–448. doi:10.1016/S0166-2236(97)01101-6.
- ↑ Piccolino M (2000). “The bicentennial of the Voltaic battery (1800–2000): the artificial electric organ”. 《Trends in Neuroscience》 23 (4): 147–151. doi:10.1016/S0166-2236(99)01544-1.
- ↑ Bernstein J (1902). “Untersuchungen zur Thermodynamik der bioelektrischen Ströme”. 《Pflüger's Arch. Ges. Physiol.》 92 (10–12): 521–562. doi:10.1007/BF01790181.
- ↑ Cole KS, Curtis HJ (1939). “Electrical impedance of the squid giant axon during activity”. 《J. Gen. Physiol.》 22 (5): 649–670. doi:10.1085/jgp.22.5.649. PMC 2142006. PMID 19873125.
- ↑ Lapicque L (1907). “Recherches quantitatives sur l'excitationelectrique des nerfs traitee comme une polarisation”. 《J. Physiol. Pathol. Gen》 9: 620– 635.
- ↑ Hodgkin AL, Katz B (1949). “The effect of sodium ions on the electrical activity of the giant axon of the squid”. 《J. Physiology》 108: 37–77.
- ↑ Neher E, Sakmann B (1976). “Single-channel currents recorded from membrane of denervated frog muscle fibres”. 《Nature》 260 (5554): 779–802. Bibcode:1976Natur.260..799N. doi:10.1038/260799a0. PMID 1083489.
* Hamill OP, Marty A, Neher E, Sakmann B, Sigworth FJ (1981). “Improved patch-clamp techniques for high-resolution current recording from cells and cell-free membrane patches”. 《Pflugers Arch.》 391 (2): 85–100. doi:10.1007/BF00656997. PMID 6270629.
* Neher E, Sakmann B (1992). “The patch clamp technique”. 《Scientific American》 266 (3): 44–51. doi:10.1038/scientificamerican0392-44. PMID 1374932. - ↑ Doyle DA; Morais Cabral J; Pfuetzner RA; Kuo A; Gulbis JM; Cohen SL; 외. (1998). “The structure of the potassium channel, molecular basis of K+ conduction and selectivity”. 《Science》 280 (5360): 69–77. Bibcode:1998Sci...280...69D. doi:10.1126/science.280.5360.69. PMID 9525859.
* Zhou Y, Morias-Cabrak JH, Kaufman A, MacKinnon R (2001). “Chemistry of ion coordination and hydration revealed by a K+-Fab complex at 2.0 A resolution”. 《Nature》 414 (6859): 43–48. doi:10.1038/35102009. PMID 11689936.
* Jiang Y, Lee A, Chen J, Ruta V, Cadene M, Chait BT, MacKinnon R (2003). “X-ray structure of a voltage-dependent K+ channel”. 《Nature》 423 (6935): 33–41. Bibcode:2003Natur.423...33J. doi:10.1038/nature01580. PMID 12721618. - ↑ Cha A, Snyder GE, Selvin PR, Bezanilla F (1999). “Atomic-scale movement of the voltage-sensing region in a potassium channel measured via spectroscopy”. 《Nature》 402 (6763): 809–813. doi:10.1038/45552. PMID 10617201.
* Glauner KS, Mannuzzu LM, Gandhi CS, Isacoff E (1999). “Spectroscopic mapping of voltage sensor movement in the Shaker potassium channel”. 《Nature》 402 (6763): 813–817. Bibcode:1999Natur.402..813G. doi:10.1038/45561. PMID 10617202.
* Bezanilla F (2000). “The voltage sensor in voltage-dependent ion channels”. 《Physiol. Rev.》 80 (2): 555–592. PMID 10747201. - ↑ Catterall WA (2001). “A 3D view of sodium channels”. 《Nature》 409 (6823): 988–999. doi:10.1038/35059188. PMID 11234048.
* Sato C; Ueno Y; Asai K; Takahashi K; Sato M; Engel A; 외. (2001). “The voltage-sensitive sodium channel is a bell-shaped molecule with several cavities”. 《Nature》 409 (6823): 1047–1051. doi:10.1038/35059098. PMID 11234014. - ↑ Yellen G (2002). “The voltage-gated potassium channels and their relatives”. 《Nature》 419 (6902): 35–42. doi:10.1038/nature00978. PMID 12214225.
- ↑ Skou J (1957). “The influence of some cations on an adenosine triphosphatase from peripheral nerves”. 《Biochim Biophys Acta》 23 (2): 394–401. doi:10.1016/0006-3002(57)90343-8. PMID 13412736.
- ↑ Hodgkin AL, Keynes RD (1955). “Active transport of cations in giant axons from Sepia and Loligo”. 《J. Physiol.》 128 (1): 28–60. PMC 1365754. PMID 14368574.
- ↑ Caldwell PC, Hodgkin AL, Keynes RD, Shaw TI (1960). “The effects of injecting energy-rich phosphate compounds on the active transport of ions in the giant axons of Loligo”. 《J. Physiol.》 152 (3): 561–90. PMC 1363339. PMID 13806926.
- ↑ Caldwell PC, Keynes RD (1957). “The utilization of phosphate bond energy for sodium extrusion from giant axons”. 《J. Physiol. (London)》 137 (1): 12–13P. PMID 13439598.
- ↑ Morth JP, Pedersen PB, Toustrup-Jensen MS, Soerensen TLM, Petersen J, Andersen JP, Vilsen B, Nissen P (2007). “Crystal structure of the sodium–potassium pump”. 《Nature》 450 (7172): 1043–1049. Bibcode:2007Natur.450.1043M. doi:10.1038/nature06419. PMID 18075585.
- ↑ Lee AG, East JM (2001). “What the structure of a calcium pump tells us about its mechanism”. 《Biochemical Journal》 356 (Pt 3): 665–683. doi:10.1042/0264-6021:3560665. PMC 1221895. PMID 11389676.
- ↑ * FitzHugh R (1960). “Thresholds and plateaus in the Hodgkin-Huxley nerve equations”. 《J. Gen. Physiol.》 43 (5): 867–896. doi:10.1085/jgp.43.5.867. PMC 2195039. PMID 13823315.
* Kepler TB, Abbott LF, Marder E (1992). “Reduction of conductance-based neuron models”. 《Biological Cybernetics》 66 (5): 381–387. doi:10.1007/BF00197717. PMID 1562643. - ↑ Morris C, Lecar H (1981). “Voltage oscillations in the barnacle giant muscle fiber”. 《Biophysical Journal》 35 (1): 193–213. Bibcode:1981BpJ....35..193M. doi:10.1016/S0006-3495(81)84782-0. PMC 1327511. PMID 7260316.
- ↑ FitzHugh R (1961). “Impulses and physiological states in theoretical models of nerve membrane”. 《Biophysical Journal》 1 (6): 445–466. Bibcode:1961BpJ.....1..445F. doi:10.1016/S0006-3495(61)86902-6. PMC 1366333. PMID 19431309.
* Nagumo J, Arimoto S, Yoshizawa S (1962). “An active pulse transmission line simulating nerve axon”. 《Proceedings of the IRE》 50 (10): 2061–2070. doi:10.1109/JRPROC.1962.288235. - ↑ Bonhoeffer KF (1948). “Activation of Passive Iron as a Model for the Excitation of Nerve”. 《J. Gen. Physiol.》 32 (1): 69–91. doi:10.1085/jgp.32.1.69. PMC 2213747. PMID 18885679.
* Bonhoeffer KF (1953). “Modelle der Nervenerregung”. 《Naturwissenschaften》 40 (11): 301–311. Bibcode:1953NW.....40..301B. doi:10.1007/BF00632438.
* van der Pol B (1926). “On relaxation-oscillations”. 《Philosophical Magazine》 2: 977–992.
* van der Pol B, van der Mark J (1928). “The heartbeat considered as a relaxation oscillation, and an electrical model of the heart”. 《Philosophical Magazine》 6: 763–775.
* van der Pol B, van der Mark J (1929). “The heartbeat considered as a relaxation oscillation, and an electrical model of the heart”. 《Arch. Neerl. Physiol.》 14: 418–443. - ↑ Evans JW (1972). “Nerve axon equations. I. Linear approximations”. 《Indiana U. Math. Journal》 21 (9): 877–885. doi:10.1512/iumj.1972.21.21071.
* Evans JW, Feroe J (1977). “Local stability theory of the nerve impulse”. 《Math. Biosci.》 37: 23–50. doi:10.1016/0025-5564(77)90076-1. - ↑ Keener JP (1983). “Analogue circuitry for the van der Pol and FitzHugh-Nagumo equations”. 《IEEE Trans. on Systems, Man and Cybernetics》 13 (5): 1010–1014. doi:10.1109/TSMC.1983.6313098.
- ↑ Hooper SL (March 2000). “Central pattern generators”. 《Curr. Biol.》 10 (5): R176. doi:10.1016/S0960-9822(00)00367-5. PMID 10713861. CiteSeerX: 10.1.1.133.3378.
웹 페이지[편집]
- ↑ “FitzHugh-Nagumo model”. 2014년 5월 24일에 확인함.
- ↑ “The Nobel Prize in Physiology or Medicine 1963” (보도 자료). The Royal Swedish Academy of Science. 1963. 2010년 2월 21일에 확인함.
- ↑ “The Nobel Prize in Physiology or Medicine 1991” (보도 자료). The Royal Swedish Academy of Science. 1991. 2010년 2월 21일에 확인함.
- ↑ “The Nobel Prize in Physiology or Medicine 1906” (보도 자료). The Royal Swedish Academy of Science. 1906. 2010년 2월 21일에 확인함.
- ↑ Warlow, Charles. “The Recent Evolution of a Symbiotic Ion Channel in the Legume Family Altered Ion Conductance and Improved Functionality in Calcium Signaling”. BMJ Publishing Group. 2013년 3월 23일에 확인함.
- ↑ “The Nobel Prize in Chemistry 1997” (보도 자료). The Royal Swedish Academy of Science. 1997. 2010년 2월 21일에 확인함.