기수법
| 기수법 |
|---|
| 개념 |
| 숫자 |
| 진법 |
기수법(記數法, numeral system)은 수를 시각적으로 나타내는 방법으로, 기수법을 통해서 나타나는 각각의 숫자는 다른 수들과 구별되는 표기 방식을 가진다. 가장 단순하고 원시적인 기수법은 1에 대한 표기만 가지고 모든 수를 표현하는 단항 기수법(unary numeral system)이며, 이후 특정 수들에 대한 표기를 가지는 명수법(命數法, sign-value notation), 숫자의 위치와 계수를 이용하여 수를 나타내는 위치값 기수법(positional system) 등의 기수법 형태로 발전하였다. 현대에서 기수법이라는 용어는 일반적으로 위치값 기수법을 의미한다.
고대부터 기수법은 문명의 발달에 따라 다양한 형태로 발전하였고, 각 문명의 기수법 체계는 그 사회의 문화와 사상을 반영한다. 초기의 숫자 체계는 각 계수(등급)의 값을 나타내는 기호를 반복하여 숫자를 나타내는 기수법(명수법)을 사용하였으며, 그리스 숫자, 이집트 숫자, 그리고 로마 숫자들이 이 경우에 속한다. 하지만 인도 문명과 중국 문명은 숫자의 위치로 계수를 나타내는 발달된 체계(위치값 기수법)로 수를 표기하였다. 특히 인도는 0의 도입을 통해서 추상적인 위치값 기수법을 완성했다는 평가를 받고 있으며 아라비아 숫자(인도 숫자)는 오늘날 전 세계적으로 가장 널리 쓰이는 기수 체계가 되었다.
현대에는 2진법, 10진법, 60진법 등 등급화의 기수(基數)에 따른 다양한 위치값 기수법이 사용되고 있다. 현대인들이 주로 사용하는 진법은 10진법으로 대부분의 숫자들은 모두 10진법으로 표기된다. 그러나 컴퓨터와 같이 비교적 간단한 표기 체계가 필요한 분야에서는 2진법도 유용하게 사용되고 있으며, 시간 표기나 각도 측정 등에서는 60진법이 이용되는 등 현대 사회에서는 다양한 진법이 복합적으로 응용된다.
종류[편집]
단항 기수법(1진법)[편집]
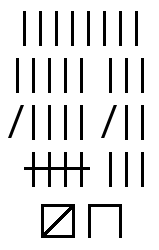
가장 원시적인 기수체계는 단항 기수법으로서, 단위 수를 수직선, 원, 또는 점 등의 기호를 반복하는 방식으로 숫자를 나타낸다. 예를 들어 만약 1을 나타내는 단위 기호가 |이라면 5는 |||||, 10은 ||||||||||로 표기한다. 초기의 단항 기수법에서는 숫자를 나타낼 때 단위 기호를 동일선 상에서 표기하였으나, 일직선의 기호들로 나타낸 숫자들은 사람들의 눈에 쉽게 들어오지 않았으며, 이에 따라 시간이 지나면서 한 줄에 있는 기호가 특정한 개수를 넘으면 다음 줄로 넘어가는 방식으로 숫자를 쓰기 시작했다. 학자들에 따르면 일렬로 나열된 단위 기호가 4개를 넘으면 쉽게 숫자를 인식하지 못하기 때문에 단항 기수법에서 한 줄에 존재하는 단위 기호는 최대 4개인 것이 일반적이라고 한다. 실제로 이집트 인이나 크레타섬 주민들의 경우 초기 단항 기수법에서 한 줄에 단위 기호를 4개씩 표기하였으며, 바빌로니아 인이나 페니키아 인들도 3분 원칙을 채택하여 실제 고대 문명의 단항기수법에서도 4의 법칙을 확인할 수 있다.[1] 또한 어떤 문명은 아예 숫자 5에 대한 기호를 만들어 초기 단항 기수법에서 발생했던 숫자 인식의 어려움을 극복하고자 하였다.
명수법[편집]
단항 기수법 체계는 단위 수(1)을 나타내는 기호 하나만을 반복적으로 배열하여 숫자를 표현하기 때문에 큰 수를 나타내기에는 한계가 있다. 때문에 단위 수뿐만 아니라 이보다 더 큰 특정한 수들에 대해서도 기호를 붙였는데, 이러한 방법을 명수법이라고 한다. 명수법을 이용해서 숫자를 표현하는 경우 단항 기수법에 비해서 큰 수를 간결하게 표현할 수 있게 된다. 예를 들어서 1을 나타내는 기호가 |, 10을 나타내는 기호를 @, 100을 나타내는 기호를 %라고 하자. 이 명수법에서 425는 %%%%@@|||||, 145는 %@@@@|||||, 57은 @@@@@||||||| 등의 방식으로 나타낸다. 고대 이집트 숫자와 로마 숫자는 명수법을 바탕으로 한 기수 체계를 형성한 대표적인 수 표기 방식이다.
위치값 기수법[편집]
인류의 기수법 체계는 단항 기수법과 명수법을 거쳐 위치값 기수법(Positional notation)으로 발전하였으며, 이전의 두 체계와 달리 위치값 기수법에서는 숫자의 위치가 계수를 의미한다. 현대에 사람들이 사용하는 숫자 체계는 아라비아 숫자에 근거한 10진법 위치값 기수 체계이다. 예를 들어서 1524라는 숫자는 (1×103) + (5×102) + (2×101) + (4×100)로 표현되며, 이 표기법에서 등급화된 수 10은 100, 101, 102, 103 등의 형태로 찾을 수 있다.
일반적으로, 위치값 기수법으로 나타낸 수 z를 수식으로 표현하면 아래와 같다.
- 또는
위 식에서 x는 등급화된 기수를 의미하며 기수의 거듭제곱들, 즉 를 기수 x에 대한 계수(階數)라고 한다. 이에 따라 등급화된 기수 x에 따라수 위치값 기수법을 x진법이라고 한다. 예컨대 등급화된 수가 2이면 2진법, 10이면 10진법, 60이면 60진법이라고 말한다. 위에서 들은 예인 1524는 10진법 체계로 표시된 숫자이다. (1)과 (2)의 끝 항에는 기수의 거듭제곱(계수(階數))없이 로 표기되는데, 이는 끝항에서 계수(階數)가 이기 때문에 생략된 것이다.
계수(係數) 는 해당 위치의 계수(階數) 의 개수를 나타내는 숫자이다. 로서 가능한 수는 항상 기수 1, 2, 3, ... , (x-1)까지 x로 등급화된 기수 체계에서 x-1개가 존재한다. 위치값 기수법으로 수를 표현하는 경우 특정한 위치가 수의 표현에서 필요하지 않는 경우가 생기는데, 이 때 그 위치가 의미를 가지지 않는다는 것을 나타내기 위해서 0의 개념이 필요하다. 인도의 10진법 숫자 체계와 바빌로니아의 60진법 숫자 체계는 대표적인 위치적 기수법 체계인데, 일부 문명은 위치의 공백을 나타내기 위한 기호 0을 고안하였다.
고대 문명의 기수법[편집]
바빌로니아 문명의 기수법[편집]
바빌로니아식 60진법[편집]

바빌로니아 문명에서 기수법이 고안된 것은 함무라비 왕 직전이라고 전해지고 있으며, 비슷한 시기에 발전하였던 기수 체계들과 달리 위치적 기수법을 사용하였다. 바빌로니아 기수법은 오늘날 가장 널리 사용되는 10진법이 아닌 60진법을 토대로 하여 한 자리에 올 수 있는 계수(係數)는 1부터 59까지 총 59개였다. 또한 숫자의 자릿수는 60에 대한 계수()를 의미한다.
바빌로니아 기수 체계에서는 59개의 계수를 단위 수 1을 나타내는 '못![]() ' 모양의 문자와 10에 해당하는 '서까래
' 모양의 문자와 10에 해당하는 '서까래![]() ' 두 가지 기호의 조합으로 나타내는데, 그 형태들이 못과 쐐기에서 따왔다고 하여 설형문자라고 말한다. 1부터 59까지의 수는 이 '못'과 '서까래'를 반복하여 표시하였다. 예를 들어 55는 못 5개와 서까래 5개로 표기하고 14는 못 4개의 서까래 1개로 나타낸다. 그러나 60을 넘어서면 위치값 기수법에 근거하여 두 자리 이상으로 수를 표시하였는데, 몇 가지 수를 바빌로니아식 기수법으로 나타내면 아래와 같다.
' 두 가지 기호의 조합으로 나타내는데, 그 형태들이 못과 쐐기에서 따왔다고 하여 설형문자라고 말한다. 1부터 59까지의 수는 이 '못'과 '서까래'를 반복하여 표시하였다. 예를 들어 55는 못 5개와 서까래 5개로 표기하고 14는 못 4개의 서까래 1개로 나타낸다. 그러나 60을 넘어서면 위치값 기수법에 근거하여 두 자리 이상으로 수를 표시하였는데, 몇 가지 수를 바빌로니아식 기수법으로 나타내면 아래와 같다.
- 75: 바빌로니아식 표기 - (1;15)[못 1개 ; 서까래 1개와 못 5개]
- 1000: 바빌로니아식 표기 - (16;40)[서까래 1개와 못 6개 ; 서까래 4개]
- 400: 바빌로니아식 표기 - (6;40)[못 6개 ; 서까래 4개]
여기에서 바빌로니아 기수법은 위치적 기수 체계(60진법)를 기본 바탕으로 설형문자로 계수(係數)를 나타내는 과정에서 10개의 못을 서까래 1개로 나타내는 등의 부가적인 원칙을 채용한 복합적인 구조였음을 확인할 수 있다. 추가적으로, 아래의 기록에서도 바빌로니아 문명이 60진법을 사용했다는 것을 쉽게 확인할 수 있다.
마르듀(Marduk) 신께서는 바빌로니아를 저버리는 기간으로 70년(못 1개;서까래 1개)이라는 수를 운명의 대장에도 기록하신 후, 관대하게도 자신의 결심을 바꾸었다. 신께서는 숫자를 바꾸어 놓으셨고, 그렇게 해서 이 도시를 단지 11년(서까래 1개와 못 1개)만에 다시 돌보도록 하셨다[2]
바빌로니아 기수법의 한계[편집]
바빌로니아 문명은 위치적 기수법을 사용하였지만, 오늘날 0의 역할처럼 특정한 위치가 수의 표현에서 의미가 없음을 나타내는 기호가 특별히 존재하지 않아 숫자 표기의 애매모호함을 피할 수 없었다. 예컨데 바빌로니아 기수법에 의하면 2는 (못 2개), 61은 (못 1개;못 1개)로 표시하지만, 두 숫자 모두 못 2개의 연속적인 배열로 표현되기 때문에 혼동을 일으킨다. 이런 문제점을 인식한 일부 바빌로니아의 서기들은 혼동을 피하고자 자릿수 사이의 띄어쓰기를 명확하게 하여 수를 표기하기도 하였지만, 종종 신중하지 못한 서기들이 띄어쓰기를 제대로 하지 못해 숫자 표기에서 모호함은 계속되었다. 이처럼 초기 바빌로니아 기수법의 근본적인 한계는 바로 '없음'을 나타내는 기호 자체가 없었다는 것이다. 하지만 현대 학자들은 바빌로니아 학자들이 그들의 애매한 위치적 기수 체계에 별다른 불편함을 느끼지 않았다고 생각하고 있으며, 이 체계는 바빌로니아 문명이 존재했던 오랜 시간동안 지속되었다.
바빌로니아 기수법에서 '없음'(특정 위치의 무의미성)의 기호가 나타난 것은 기원전 3세기 경으로, 이는 역사에서 가장 오래된 '없음'의 개념이다. 그러나 없다는 것을 의미하는 바빌로니아식 기호와 오늘날 우리가 사용하는 0의 의미에는 약간의 차이가 있다. 바빌로니아 사람들은 그들이 만든 '없음'의 기호를 양이 아무것도 없는 것을 표현하는 데 쓰지 않고 단지 특정 위치에서의 공백을 나타낼 때만 사용하였다. 현대적으로 표현하면, 0이라는 기호를 102, 4006 등 숫자를 표기하는 과정에서는 썼지만 30-30이라는 연산에 대한 답으로서 0을 쓰지는 않았다는 것이다.(대신 "다 떨어졌다", "없어졌다" 등의 문장 표현을 사용했다고 한다.) 이처럼 바빌로니아 사람들은 위치에서의 공백과 양적으로 없는 것을 다르게 간주하였다. 비록 완전하지는 않지만, 바빌로니아의 기수 체계는 최초로 위치적 기수법을 도입하고 공백을 나타내는 기호를 처음으로 발명했다는 점에서 충분히 수학사적 가치를 가진다.
고대 이집트 문명의 기수법[편집]
고대 이집트의 10진법[편집]
고대 이집트 문명에서 기수법이 고안된 것은 약 기원전 3000년부터라고 전해지고 있으며, 이 기수법은 기원후 1000년 초까지 고대 이집트에서 사용되어왔다. 고대 이집트 기수법은 현대인들이 주로 쓰는 10진법을 사용하였으며, 표기 방법으로는 명수법을 기초로 하고 있다. 10진법을 사용함에 따라 1, 10, 100, 1000 등의 숫자들을 특정한 기호로 표기하였는데, 이러한 기호들에는 모두 특정 사물을 본 따서 만든 상형문자가 사용되었다. 1은 막대기, 10은 발뒤꿈치 뼈, 100은 감아 놓은 밧줄, 1000은 연꽃 줄기, 10000은 손가락, 10만은 개구리 혹은 올챙이, 100만은 두 손을 위로 올린 사람 등의 모습으로부터 상형문자를 고안했는데, 기호 관념을 갖추고 있었던 이집트 문화 속에서 이들 기호가 어떤 신비주의적 중요성을 띄었던 것이라고 추측하는 이들도 있다.[3] 예를 들어 100만의 경우, 당시 고대 이집트에서 100만이란 숫자는 어마어마하게 크고 거대한 수였기에 100만에서 느껴지는 경외감을 사람이 두 손을 위로 들어 신을 경배 하는듯한 모습으로 표현한 것이라고 할 수 있다는 것이다. 이러한 상형문자를 이용한 기수법은 자리마다 다른 기호가 필요하므로 모든 수를 표현하려면 상형문자 기호가 무한히 많아야 했겠지만, 실질적으로 고대 이집트에서 10만보다 큰 수가 필요한 경우는 드물었기에 이러한 기수법이 오랜 기간 유지되었던 것이다. 아래의 표는 고대 이집트에서 숫자에 사용된 상형문자를 정리한 것이다.
| 숫자 | 1 | 10 | 100 | 1,000 | 10,000 | 100,000 | 100만, 혹은 많다 | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 상형 문자 |
|
|
|
|
|
혹은
|
| ||||||||||||||||
| 묘사 | 막대기 | 발뒤꿈치 뼈 | 감아 놓은 밧줄 | 연꽃 줄기 | 손가락 | 올챙이 혹은 개구리 |
두 손을 위로 올린 남자 |
예를 들어, 이집트 공화국 동부에 있는 카르낙이라는 곳에서 발견된 돌에 새겨진 아래의 기호는 4622를 뜻하는 기호이다.
|
이러한 숫자 기호들은 위에서 아래, 아래에서 위, 왼쪽에서 오른쪽으로, 또는 오른쪽에서 왼쪽으로 쓰여 왔는데 오른쪽에서 왼쪽으로 쓸 때는 기호가 뒤집혀서 쓰였다. 위의 예제는 왼쪽에서 오른쪽, 그리고 위에서 아래로 쓰인 경우이다.
신관서체의 숫자 기호[편집]
행정상과 회계 상의 문서들은 상형문자처럼 돌에 새겨지는 것이 아니라 파피루스 또는 도편에 기록되었는데, 이 경우 고대 이집트인들은 '신관서체'라는 필기체를 사용하였다. 신관서체의 숫자 기호는 기존에 사용되던 숫자 기호와는 사뭇 다른데, 이를 사용한 흔적은 이집트 초기왕조 시기에 발견된 문서들에서 찾아 볼 수 있다. 특히, 이집트 고 왕국 시대 때의 아부시르에서 발견된 파피루스들은 신관서체의 숫자 기호가 사용된 중요한 문서들이다.
신관서체에서의 기수법은 기존의 기수법과는 다르게 1부터 9, 10부터 90까지의 10의 배수, 100부터 900까지의 100의 배수, 1000부터 9000까지의 1000의 배수 등에 각기 다른 기호를 붙여서 사용하였다. 예를 들어 9999의 경우, 기존의 기수법으로는 36개의 기호(1 9개, 10 9개, 100 9개, 1000 9개)가 필요하지만 신관서체로 9999를 기록할 때는 오로지 4개의 기호(9 1개, 90 1개, 900 1개, 9000 1개)만이 필요하다.
신관서체의 숫자 기호를 사용하여 저술된 수학적인 문서들 중 가장 저명한 두 개의 파피루스가 바로 '모스크바 파피루스' 와 '린드 파피루스'이다.
중국 문명의 기수법[편집]
중국의 숫자체계는 특정 숫자들을 발음할 때 쓰이던 중국의 문자들로 구성되어 있는데, 이 숫자 체계는 과거 한자 문화권에 포함되어있던 일본, 한국에서도 사용되었다. 이러한 숫자 체계는 영어처럼 발음에 쓰이던 문자들로 구성되어있기 때문에 아라비아 숫자 등에서 쓰이던 위치 기수법이 사용되지 않았다. 중국에서 숫자를 나타낼 때 쓰였던 문자들은 다음과 같이 크게 4가지로 나눌 수 있다; 상 왕조 시대의 숫자, 청동기 시대의 숫자, 막대 숫자(산가지), 표준 숫자.
상 왕조 시대의 숫자[편집]

상 왕조 시대 이후의 중국 숫자들은 대부분이 기원전 14세기인 상 왕조 시대 때 쓰이던 숫자에서부터 비롯되었다. 갑골 문자로 알려진 상 왕조 시대의 숫자는 거북이의 등껍질과 동물의 뼈에서 처음 발견이 되었다.
청동기 시대의 숫자[편집]

청동기 시대의 숫자들 중 1, 2, 3, 4, 10, 11, 12, 13 등의 숫자들에 쓰이던 기호들이 이후의 중국 숫자인 막대 숫자(산가지)에도 그대로 쓰였다.
산가지[편집]
산가지는 각 숫자들을 막대기로 표현하였는데, 혼란을 방지하기 위해 수직과 수평을 번갈아 가면서 사용하였다. 일반적으로, 수직 막대는 한 자리 수, 백의 자리 수, 만의 자리 수 등을 표현하는데 사용되었고, 수평 막대는 십의 자리 수, 천의 자리 수, 십만의 자리 수 등을 표현하는데 사용되었다. 산가지 숫자 체계는 전국 시대부터 16세기까지 쓰였는데 주로 상인, 수학자, 천문학자들에 의해 사용되었다.
| 七 | 一 | 八 | 二 | 四 |
|---|---|---|---|---|
| 万 | 千 | 百 | 十 | 步 |
표준 숫자[편집]
중국의 표준 숫자는 크게 두 가지로 나뉜다. 일반적인 생활에서 쓰이는 숫자와, 갖은자라 불리는 경제 관련 문서에서 쓰이는 숫자가 바로 그것이다. 경제 관련 문서에는 일반적인 생활에서 쓰이는 숫자와 다른 숫자를 썼는데, 그 이유는 일부 중국 숫자의 특성 상 획을 몇 개 추가하거나 수정하면 다른 수를 뜻하는 문자가 되어버리기 때문이다. 예를 들어, 三十(30)의 경우, 三에 두 획을 그으면 五, 十에 한 획을 그으면 千이 되어 三十(30)이 五千(5000)으로 바뀌어 버린다. 일반적인 생활에서는 이와같이 숫자를 바꿀 필요가 없지만, 경제 관련 문서에서는 위조가 될 가능성이 매우 높아지게 된다. 따라서, 중국 표준 숫자에서 경제 관련 문서에 쓰이는 숫자는 일상 생활에서 쓰이는 숫자에서 수정 가능한 숫자들을 몇 개 바꾼 것을 사용한다.
| 경제 관련 문서 | 일반적인 문서 | 크기 | 병음 |
|---|---|---|---|
| 零 | 〇 | 0 | líng |
| 壹 | 一 | 1 | yī |
| 貳 (번) 또는 贰 (간) |
二 | 2 | èr |
| 叄 (번) 또는 叁 (간) |
三 | 3 | sān |
| 肆 | 四 | 4 | sì |
| 伍 | 五 | 5 | wǔ |
| 陸 (번) 또는 陆 (간) |
六 | 6 | liù |
| 柒 | 七 | 7 | qī |
| 捌 | 八 | 8 | bā |
| 玖 | 九 | 9 | jiǔ |
| 拾 | 十 | 10 | shí |
| 佰 | 百 | 100 | bǎi |
| 仟 | 千 | 1,000 | qiān |
| 萬 | 萬 (번) 또는 万 (간) |
104 | wàn |
| 億 | 億 (번) 또는 亿 (간) |
108 | yì |
중국의 일부 지역에서는 표준 숫자에서 일부분 바뀐 숫자들을 사용한다.
| 바뀐 숫자 | 크기 | 병음 | 표준 숫자 |
|---|---|---|---|
| 幺 | 1 | yāo | 一 |
| 兩(번) 또는 两(간) |
2 | liǎng | 二 |
| 呀 | 10 | yā | 十 |
| 念(번) 또는 廿(간) |
20 | niàn | 二十 |
| 卅 | 30 | sà | 三十 |
| 卌 | 40 | xì | 四十 |
| 皕 | 200 | bì | 二百 |
그리스 문명의 기수법[편집]
그리스 숫자[편집]
그리스 기수법은 그리스 문자를 사용하여 숫자들을 표현하는 방식이다. 고대 그리스에 알파벳이 만들어지기 전에 사용되던 숫자 체계를 '에게 숫자'라고 부르는데, 이 숫자 체계에는 1, 10, 100, 1000 그리고 10000에 해당하는 기호들이 존재하여 그 기호들의 조합으로 숫자를 표현하였다.
| = 1, – = 10, ◦ = 100, ¤ = 1000, ☼ = 10000
'에게 숫자' 이후 고대 그리스인들은 두 가지의 숫자 체계를 사용했는데, 둘 중 먼저 만들어진 것은 수를 순서대로 배열한 뒤 로마 숫자처럼 무리를 지어 사용하는 숫자 체계이었다. 이를 '열(列) 숫자' 혹은 '아티카 숫자'라고 부르는데, 이 숫자 체계에는 1, 10, 100, 1000 그리고 10000의 계수를 나타내는 개별적인 기호들이 존재한다. 또한, 위와 같이 10진법의 집단화를 나타내는 기호들 외에, 5에 의한 집단화를 나타내는 기호들도 존재하는데, 여기서 1을 제외한 나머지 계수들(10, 100, 1000, 10000)을 나타내는 기호들은 각 계수를 나타내는 수 단어의 첫 글자들이며, 5에 의한 집단화를 뜻하는 기호들은 5를 나타내는 수 단어 pente의 첫 글자인 <Π>를 사용하여 나타내어졌다.[4]
Ι = 1, Π = 5, Δ = 10, ΠΔ = 50, Η = 100, ΠΗ = 500, Χ = 1000, ΠΧ = 5000, Μ = 10000, ΠΜ = 50000
'열(列) 숫자' 혹은 '아티카 숫자'에 이어서 그리스에 알파벳으로 이루어지고 유사십진법을 사용하는 학문적인 숫자 체계가 등장하였는데, 바로 '이오니아 숫자'이다. 기원전 5세기에 처음으로 등장한 '이오니아 숫자'는 기원전 1세기부터 그리스의 도시 중 하나인 아테네의 공식 숫자 체계로 사용되었는데, 이 숫자 체계는 각 일의 자리(1, 2, ..., 9)와 십의 자리(10, 20, ..., 90), 백의 자리(100, 200, ..., 900)를 나타내기 위해 각각에 별도의 문자를 할당하였다. 여기에는 총 27개의 문자가 필요한데, 그리스 문자인 24자 이외에 지금은 쓰이지 않는 옛 문자인 디감마 ϝʹ 혹은 스티그마 ϛʹ(6), 코파 ϟʹ (90), 삼피 ϡʹ(900)이 사용되었다.[5]
| 기호 | 값 | 기호 | 값 | 기호 | 값 | ||
|---|---|---|---|---|---|---|---|
| αʹ | 1 | ιʹ | 10 | ρʹ | 100 | ||
| βʹ | 2 | κʹ | 20 | σʹ | 200 | ||
| γʹ | 3 | λʹ | 30 | τʹ | 300 | ||
| δʹ | 4 | μʹ | 40 | υʹ | 400 | ||
| εʹ | 5 | νʹ | 50 | φʹ | 500 | ||
| ϝʹ 혹은 ϛʹ 혹은 στʹ | 6 | ξʹ | 60 | χʹ | 600 | ||
| ζʹ | 7 | οʹ | 70 | ψʹ | 700 | ||
| ηʹ | 8 | πʹ | 80 | ωʹ | 800 | ||
| θʹ | 9 | ϟʹ | 90 | ϡʹ | 900 |
매우 큰 수의 표기[편집]
그리스인들은 매우 큰 수를 표기하기 위해 '만' 단위의 묶음을 이용했는데, '만'을 나타내는 기호로 (Mʹ)을 사용하여 큰 수를 표기하였다. 예를 들어, 45,820,709의 경우에는 아래와 같이 표기를 하였다.
Mʹ을 사용하여도 나타낼 수 없을 만큼 큰 수를 표현할 때에는, '억'을 나타내는 기호인 (ΜΜʹ)가 사용되었다. 아르키메데스의 논문인 '모래알을 세는 사람'에서 아르키데메스는 우주를 모두 모래로 채울 때 모래알의 개수는 몇 개가 될 것인가에 대해 다루었다. 아르키메데스는 그 모래알의 개수보다 큰 수는 다룰 필요가 없다고 하여 그 모래알의 개수를 수에 있어서의 위쪽 경계선으로 지정하였는데, 그 모래알의 개수를 표현하기 위해 그는 새로운 수 표현 체계를 만들어야 했다. 조는 MMMʹ과 같이 쓸 수 있다.
마야 문명의 기수법[편집]
마야 인들의 20진법[편집]

중앙아메리카에서 번성하였던 마야 문명은 독자적으로 기수법 체계를 발전시켜왔다. 5-6 세기 경 천문학과 점성술에 관련된 마야 인들의 기록인 '드레스드 처방전'(Codex de Dresde)에는 마야 승려 사회에서는 20으로 등급화된 위치적 기수 체계(20진법)가 존재했음을 알 수 있는 기록이 남아있으며,[6] 이들은 0에 대한 개념도 가지고 있었다. 마야 문명의 기수법에서는 총 19개의 수가 점과 선 등의 단순한 상징들로 표상되며, 점은 단위 수 1을 나타내고 가로선 또는 세로선은 5를 의미한다. 점 5개는 선 한 개로 대체되어서 5를 나타내고, 따라서 한 자릿수에서 나타날 수 있는 점은 최대 4개가 되는 것이다. 또한 마야 숫자는 가로와 세로 두 방향으로 쓸 수 있다.(가로의 경우 왼쪽에서 오른쪽으로, 세로의 경우 위쪽에서 아래쪽으로 읽는다.)
그러나 마야 문명의 기수법은 일반적인 위치적 기수법과 부분적으로 차이를 보인다. 마야의 기수법은 20진법을 기반으로 하고 있기 때문에 원칙적으로 끝자리부터 3번째 숫자의 계수(階數)는 는 가 되어야 하지만, 마야의 학자들에게 세 번째 숫자는 360을 의미하는 것이었다. 그리고 4번째의 숫자의 계수(階數)부터는 다시 20진법의 정의대로 계수가 20의 거듭제곱의 형태로 나타난다. 예를 들어 (13;1;5;14)라는 마야 숫자를 그들의 위치적 기수법에 따라서 분석하면 가 된다. 이런 변칙은 마야 숫자가 모든 수를 나타낼 수 없게 되는 원인이 되었다.
마야 문명의 기수 체계와 천문학[편집]
마야 문명의 기수법의 셋째 자리 숫자에서 나타나는 변칙의 원인은 마야의 천문학에서 찾을 수 있다. 사실 마야의 천문학에서 발전된 날짜 체계는 그 단위가 '하루'였으며, 1년은 360일로 어림잡고 있었다. 그리고 마야인들은 보통 마야 기원 이후 흐른 시간을 (끝자리부터)kins('일'), unials(20일을 나타내는 '월'), tuns(360일로 구성된 '년'), katuns(20년 주기), baktuns(400년 주기)로 하여 총 다섯 개의 숫자로 표현하였다.[7] 마야 기수 체계의 발명된 목적은 일상 생활에서의 셈이 아니라 시간의 계산과 천문학적 관찰 과정에서의 필요성이었다. 그러므로 마야의 천문학에서 발전된 날짜와 시간 표시 체계는 마야의 기수법에 영향을 줄 수밖에 없었다. 마야 시간 표기법에서 세 번째 숫자는 360일로 구성된 1'년'을 나타내는 것이었고, 때문에 마야 문명의 기수 체계에서 세 번째 숫자의 계수(階數)는 400이 아닌 360이 되었다.
마야 기수 체계에 0을 의미하는 기호가 존재하는 이유도 마야인들의 신에 대한 두려움 및 신비주의에서 비롯된 것이다. 먀야의 시간 표기 체계에서 5개의 숫자는 각각 신을 대변하는 것이었다. 마야 학자들은 시간을 표기할 때 필요가 없다는 이유로 다섯 자리 숫자 중에서 일부를 나타내지 않으면 그것은 신에 대한 모독이라고 생각하였고, 때문에 비록 자릿수가 공백이 될 지라도 그것을 표시할 기호를 발명하게 되었다. 또한 공백을 나타내는 기호의 발명에는 문자를 배치하는 과정에서 균형미에 대한 마야인들의 염려도 어느정도 기여하였다. 결국 신에 대한 신비주의적인 두려움과 미학적인 걱정이 마야인들로 하여금 '공백'에 대한 기호를 창조하게 만든 것이다.
인도 문명의 기수법 체계[편집]
초기 인도 문명의 기수법[편집]
기록에 의하면 북인도 지방에 살고 있던 초기 인도인들은 원시적인 기수법을 사용하였으며, 그 체계는 명수법을 따르고 있다. 또한 이 시기에 사용된 기호들은 오늘날 사람들이 사용하고 있는 아라비아 숫자의 기원이 되었다. 인도 숫자는 개발된 지역에 따라서 그 표기에 어느 정도 차이가 있으며, 동아라비아 숫자(아라비아-인도식),이에 대한 변형인 동아라비아-인도식 숫자, 데바나가리(Devanagari) 숫자, 타밀 숫자 등의 종류가 있다. 일반적으로 인도 기수 체계에서 존재하였던 기호가 나타내는 수는 아래와 같다.
- 1, 2, 3, 4, 5, 6, 7, 8, 9
- 99이하의 10의 배수 : 10, 20, 30, 40, 50, 60, 70, 80, 90.
- 999 이하의 100의 배수 : 100, 200, 300, 400, 500, 600, 700, 800, 900
- 9999 이하의 1000의 배수 : 1000, 2000, 3000, 4000, 5000, 6000, 7000, 8000, 9000
- 99999 이하의 10000의 배수 : 10000, 20000, 30000, 40000, 50000, 60000, 70000, 80000, 90000
각각의 수는 위의 단위 수들을 나타내는 기호를 반복하여 나열하는 방식으로 표기되었다. 그리고 이 중에서 1부터 9까지의 기호는 이후 '0'을 나타내는 기호의 발명과 함께 위치값 기수법에서 계수를 나타내는 숫자로 발전하게 된다.
문자 표기법[편집]
원시적인 인도의 기수법은 큰 수를 나타내기 매우 어려웠기 때문에, 이후 인도인들은 산스크리트어로 수를 나타냄으로써 표기의 번거러움을 줄이고자 하였다. 우선 기본 수인 1부터 9까지 9개의 숫자와 10의 거듭제곱수에 명칭을 붙이고, 기본 단위부터 시작해서 거듭제곱수들과 그에 대한 계수(係數)를 작은 수에서 큰 수로 배열하였다. 수들은 각기 다른 문자들로 표현되었으며, 10, 100, 1000 등의 거듭제곱수들과 1부터 9까지의 수는 아래의 표처럼 각각의 문자로 표기되었다.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| eka | dvi | tri | catur | parica | sat | sapta | esta | nava |
| 10 | 100 | 1000 | 10000 | 100000 | 1000000 | 10000000 | 100000000 | 1000000000 |
| dasa | sata | sahasra | ayuta | laksa | prayuta | koti | vyarbuda | padma |
예를 들어서 4232는 인도의 산스크리트어 문자 표기 기수법에 의해 dvi tri dasa dvi sata catur sahasra(이, 삼십, 이백, 그리고 사천)와 같이 나타낼 수 있다. 이 기수법은 오늘날의 구두 기수법과 달리 작은 단위수부터 읽는다. 인도의 문자 기수법은 인도 문명의 전통적, 신화적 관념을 반영하기도 하였다. 인도 학자들은 숫자 하나를 나타나는데 특별한 의미들을 부여받은 여러 가지 문자들을 동시에 사용하였는데, 예를 들어 1을 의미하는 eka는 '시작', '몸통', '제일의 아버지' 등의 의미를 나타는 문자로 대체 가능했고 2의 dvi는 전통과 신화 등에서 둘을 의미하는 '쌍둥이 신', '눈', '팔', '날개' 동의어들이 그 역할을 대신할 수 있었다. 실제로도 인도 문명에서 후가 및 천문학 관련 기록은 대체로 이런 방식으로 표현된 수들로 구성되어 있는 시로 전해 내려오고 있다.[10]
위치값 기수법의 등장[편집]
산스크리트어 표기법이 발달한 이후에도 인도 학자들은 더 간단하게 수를 나타내기 위해서 노력하였고, 이는 그들로 하여금 계수를 나타내는 명칭을 제거하고 자릿수의 위치가 그 역할을 대신하는 위치값 기수법을 고안하게 하였다. 또한 이러한 위치 기수 체계에서는 특정한 자릿수 단위가 '공백'임을 나타낼 수 있는 기호가 필요하였으며, 인도 학자들은 이에 대한 기호로 sunya를 사용하기 시작하였다.[11] 이처럼 인도 숫자 체계는 위치값 기수법의 사용 및 '공백'을 나타내는 기호 확립 등 현대적인 기수법의 구성의 발판을 마련하기 시작하였다.
그러나 이 방식은 덧셈과 곱셈 등의 산술연산을 행하기는 상당히 어렵다는 문제점을 가지고 있었고, 때문에 1부터 9까지의 기본 수는 원시적인 인도 기수법에서 사용하던 기호를 사용하고 위치의 구분을 선으로서 구분하는 기둥 셈틀을 사용하기 시작하였다. 기둥 셈틀은 오른쪽에서부터 시작해서 첫 번째는 1단위, 두 번째는 10단위, 세 번째는 100단위의 방식으로 나타내었으며 특정 위치에 숫자가 존재하지 않는 경우 그 위치는 빈 칸으로 남겨두었다. 예를 들어서 132는 1|3|2로, 1300은 1|3| | , 2011은 2| |1|1등의 방식으로 나타냈다.
인도에서 '0'의 개념과 위치 기수 체계의 본격적으로 확립되기 시작한 것은 5세기 경 부터이다. 이 시기부터는 10진법으로 숫자를 표현한 기록이 존재하며, 인도 숫자는 학자들의 세계에서 대중들에게로, 또 인도를 넘어 캄보디아와 베트남 등의 주변 지역으로까지 확산되었다.[12] 인도 문명은 이후 위치적 기수법에서 특정한 위치에 대한 '공백'과 양적으로 '없음'을 통합적으로 의미하는 '0'이라는 기호를 발명하는 경지에 이르게 된다. 작은 수를 왼쪽에 위치시키던 방식을 버리고 오늘날과 같이 오른쪽에 위치시키는 방법을 사용한 것도 이 시기부터이다.
| 표현 방식 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 아라비아-인도식 | ٠ | ١ | ٢ | ٣ | ٤ | ٥ | ٦ | ٧ | ٨ | ٩ |
| 동 아라비아-인도식 (페르시아 및 우르드) |
۰ | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ |
| 데바나가리(Devanagari) (Hindi) |
० | १ | २ | ३ | ४ | ५ | ६ | ७ | ८ | ९ |
| 타밀(Tamil) | (빈칸) | ௧ | ௨ | ௩ | ௪ | ௫ | ௬ | ௭ | ௮ | ௯ |
0의 발명과 위치값 기수법의 발전[편집]
위치값 기수법은 한정된 숫자들만을 이용해서 모든 수를 나타낼 수 있는 매우 효율적인 기수법이었다. 바빌로니아 문명, 마야 문명, 중국 문명 등은 이 기수 체계를 사용할 줄 알았지만, 현대에 사용되고 있는 위치값 기수법과 비교했을 때 몇 가지 한계가 존재하였다. 바빌로니아 문명은 60진법을 1과 10을 나타내는 설형 문자의 조합으로 나타내어서 기록의 번거로움을 피할 수 없었고, 마야 문명도 비슷하게 20진법에서 숫자를 1과 5에 대한 기호의 조합으로 표기해 쓰기가 어려웠다. 또한 마야 인들은 기수법과 천문학의 밀접한 연관성으로 인해서 세 번째 숫자의 계수를 400이 아닌 360으로 나타내서 모든 수를 나타낼 수도 없었다. 중국 문명 또한 십진법 표기에 필요한 1에서 9까지의 단위를 각기 다른 기호로 표현한 것이 아니라 특정 단위의 반복으로 표현하였다.
위치값 기수 체계가 등장하면서 숫자의 위치가 갖는 의미는 매우 중요해졌지만, 공백을 나타내기 위해서 띄어쓰기를 하는 등의 기존의 방식으로는 표기의 애매모호함을 피할 수 없었다. 때문에 바빌로니아 문명과 마야 문명은 해당 위치의 '공백'을 의미하는 기호를 개발해 냈다. 하지만 이들은 양이 존재하지 않는 것과 위치의 공백을 서로 다른 개념으로 생각하였고, 그들의 기수 체계에서 산술적인 연산을 시행하는 것에도 한계가 있었다.
현대적인 위치적 기수법을 향한 발전의 발판을 마련한 것은 인도 문명이었다. 그들은 1에서 9까지의 단위 수들은 각기 다른 단순한 기호로 표현하였으며, 위치의 공백과 무의미한 양을 통합적으로 나타낸 기호 '0'을 발명해냈다. 이는 인도 숫자(아라비아 숫자)가 중국이나 마야, 바빌로니아 문명의 숫자와 달리 널리 퍼져 산술과 대수학의 발전을 가져왔으며, 오늘날 아라비아 숫자는 바탕으로 한 위치적 기수 체계는 편리함 및 우수성을 인정받아 전 세계적으로 통용되고 있다.
한국의 기수법 역사[편집]
한자로 된 숫자[편집]
한반도에서는 고대부터 한자를 사용하였으며, 당연히 한문으로 된 숫자가 있었다. 이 당시 사용되었던 기수법은 10진법을 기반으로 하였고, 1, 2, ..., 10, 100, 1000, ... 에 해당하는 한문을 숫자로 사용하였다. 아래는 각 숫자를 나타내는 한자들이다.
一 = 1, 二 = 2, 三 = 3, 四 = 4, 五 = 5, 六 = , 七 = 7, 八 = 8. 九 = 9, 十 = 10, 百 = 100, 千 = 1000, 萬 = 10000, 億 = 100000000, 兆 = 1012, ...
11과 같은 복합된 숫자를 나타낼 때는 아래와 같이 왼쪽에서 오른쪽으로 차례대로 썼으며, 큰 수를 묶어서 표현을 할 때는 중국의 전통대로 '만'을 기준으로 하였다.
十一 = 11, 三十四 = 34, 六千九百七 = 6907, 十萬 = 100000, 百萬 = 1000000, 千萬 = 10000000
주식 숫자[편집]
현재 사용하는 아라비아 숫자와는 달리 한문으로 된 숫자는 계산용이 아닌 기록이 목적이었다. 그러므로 계산을 위해서 별도의 계산 기구가 필요한 것은 당연했다. 한반도에서도 중국의 예를 본받아 공적으로 산가지[算木, 策]을 계산기로 사용하였다. 처음에는 관료 조직의 내부 또는 사대부 층의 엘리트 사회에서만 사용했었는데 그 이유는, 조선 중기까지는 조직적인 계산 능력이 필요할 정도의 상업 활동을 할 집단은 오직 관료 체제의 내부나 극소수의 지배계층뿐이었기 때문이다. 산가지는 삼국시대부터 사용되었는데 산가지의 제도, 즉 공식 규격이 정해져 있었지만 이러한 규격은 딱히 지켜진 것이 아닌, 그저 형식상의 규격일 뿐이었다.[13]
산가지로 수를 나타내는 방법으로는 <손자산경>이라는 책에 나온 아래의 문구대로 이루어졌다.
일은 세로, 십은 가로, 백은 서고, 천은 눕고, 천과 십은 서로 우러러 보고, 만과 백은 서로 마주 대한다.

즉, 산가지를 배열할 때에는 1의 자리와 10의 자리의 수를 혼동하지 않도록 세로와 가로로 구별하면서 놓고, 이하 100의 자리의 수를 혼동하지 않도록 세로와 가로로 구별하면서 놓고, 이하 100의 자리와 만의 자리는 세로, 1000의 자리와 10만 자리 등은 가로가 되도록 세로와 가로를 번갈아 가면서 바꾼다. 산가지의 수 표시를 그대로 옮겨 쓴 것이 이른바 '주식 숫자'이다. 주식 숫자에서는 각 숫자 사이에 간격을 두지 않고 꼭 붙여서 써야하고, 빈자리는 O으로 나타내야 하며, 음수는 마지막 자리의 숫자에 빗금을 그어야했다.[14]
-
2567을 '주식 숫자'로 나타내었다.
-
23016을 '주식 숫자'로 나타내었다. 여기서 0을 O으로 표현했다는 것에 주목해야한다.
-
-732을 '주식 숫자'로 나타내었다. 여기서 음수는 마지막 자리의 숫자에 빗금을 그어야한다는 것에 주목해야한다.
호산[편집]

조선 후기에 대규모의 고리대 자본이 형성된 이후, 부기에는 '호산' 혹은 '표산'이라고 불리는 숫자가 쓰였다. 이 표기법은 주로 중국 상인들이 사용하였던 표기법인데, 개성상인이 인삼 등의 무역을 통한 중국 상인과의 교류를 통해 이 표기법을 익힌 것이라고 생각된다. '호산'은 주로 물건의 가격을 표시하기 위해 사용되었는데, 매매 및 교환물은 물론 물품의 단위 또한 이것으로 표시했으며 금액을 합계한 총액을 기재하는 데도 쓰였다.[15]
아라비아 숫자[편집]
개화기 이후, 국내에서 사용하는 숫자가 '아라비아 숫자'로 바뀌었으며 현재까지도 유지되어오고 있다. 이러한 '아라비아 숫자'를 읽는 방식에는 두 가지가 있는데, 한국어의 한자어로 읽는 방법과 고유 한국어로 읽는 방법으로 아래의 표와 같이 읽는다.
| 숫자 | 한자 | 한국어의 한자어 | 고유 한국어 |
|---|---|---|---|
| 한글 | 한글 | ||
| 0 | 零/〇 | 영 (령), 공 | - |
| 1 | 一 | 일 | 하나 |
| 2 | 二 | 이 | 둘 |
| 3 | 三 | 삼 | 셋 |
| 4 | 四 | 사 | 넷 |
| 5 | 五 | 오 | 다섯 |
| 6 | 六 | 육 (륙) | 여섯 |
| 7 | 七 | 칠 | 일곱 |
| 8 | 八 | 팔 | 여덟 |
| 9 | 九 | 구 | 아홉 |
| 10 | 十 | 십 | 열 |
| 11 | 十一 | 십일 | 열 하나 |
| 12 | 十二 | 십이 | 열 둘 |
| 13 | 十三 | 십삼 | 열 셋 |
| 14 | 十四 | 십사 | 열 넷 |
| 15 | 十五 | 십오 | 열 다섯 |
| 16 | 十六 | 십육 (십륙) | 열 여섯 |
| 17 | 十七 | 십칠 | 열 일곱 |
| 18 | 十八 | 십팔 | 열 여덟 |
| 19 | 十九 | 십구 | 열 아홉 |
| 20 | 二十 | 이십 | 스물 |
| 30 | 三十 | 삼십 | 서른 |
| 40 | 四十 | 사십 | 마흔 |
| 50 | 五十 | 오십 | 쉰 |
| 60 | 六十 | 육십 (륙십) | 예순 |
| 70 | 七十 | 칠십 | 일흔 |
| 80 | 八十 | 팔십 | 여든 |
| 90 | 九十 | 구십 | 아흔 |
| 100 | 百 | 백 | 온 |
| 1000 | 千 | 천 | 즈믄 |
| 10000 | 萬 | 만 | 드먼 / 골 |
| 100000000 | 億 | 억 | 잘 |
| 1012 | 兆 | 조 | 울 |
| 1016 | 京 | 경 | - |
| 1020 | 垓 | 해 | - |
| 1024 | 秭 | 자 | - |
| 1028 | 穰 | 양 | - |
| 1032 | 溝 | 구 | - |
| 1036 | 澗 | 간 | - |
| 1040 | 正 | 정 | - |
| 1044 | 載 | 재 | - |
| 1048 | 極 | 극 | - |
| 1052 혹은 1056 | 恒河沙 | 항하사 | - |
| 1056 혹은 1064 | 阿僧祇 | 아승기 | - |
| 1060 혹은 1072 | 那由他 | 나유타 | - |
| 1064 혹은 1080 | 不可思議 | 불가사의 | - |
| 1068 혹은 1088 | 無量大數 | 무량대수 | - |
대표적인 진법과 그 응용[편집]
2진법[편집]

2진법은 두 종류의 숫자만을 이용하여 수를 나타내는 수 체계이다. 관습적으로 0과 1의 기호를 쓰며 이들로 이루어진 수를 2진수라고 한다. 2진법이 정확히 언제부터 사용되었는지는 아무도 모르지만, 인도 학자인 핀갈라(약 기원전 5세기 ~ 2세기)가 시의 운율을 수학적으로 표현하기 위해 음절의 길고 짧음을 구분해서 마치 모스 부호처럼 표현을 했는데 이것이 여태까지 알려진 2진법이 사용된 표현들 중 최초라고 알려져 있다. 2진법은, 두 가지의 숫자만을 이용한다는 특징 때문에 논리적인 이분법과 잘 맞아떨어져 논리와 관련된 상당 부분의 수학적 표현이 2진법으로 이루어질 수 있다. 현대의 컴퓨터도 이러한 2진법의 특성을 잘 이용한 예이다. 2진법을 사용하면 논리의 조립이 간단해지고 컴퓨터 내부에 사용되는 소자가 그 특성상(켜지고 꺼짐) 2진법의 수를 나타내는데 편리하기 때문에 컴퓨터에서 보내는 디지털 신호는, 비록 신호의 길이가 길어지더라도 기본적으로 2진법 수들의 나열로 이루어져 있으며 컴퓨터 내부에서 처리하는 모든 숫자들도 기본적으로 2진법을 사용하고 있다.[16]
2진법을 이용한 계산[편집]
2진법은 2로 등급화된 위치값 기수법 체계로, 계수(階數)는 2의 거듭제곱으로 나타내며 해당 위치의 계수(係數)는 0과 1 두 가지 종류의 숫자이다. 예를 들어서 11101의 2진법 숫자는 10진수로 29와 같고 110은 10진수 6을 의미한다. 또한 2진법은 소수점 아래의 숫자까지 표기할 수 있도록 확장되었다. 즉, 소숫점 n번째 자리가 나타내는 계수(階數)는 이다. 확장 정의에 따른 2진수 110.11은 소수점 왼쪽에 있는 숫자를 십진수 6으로 나타낸 것에다 소숫점 이하의 숫자를 10진수로 변환한 를 더한 6.75와 같은 수가 된다. 이처럼 2진법은 0과 1 두 가지의 간단한 기호만으로 소수점 아래의 연산까지 포함하는 사칙연산을 비교적 단순한 방법으로 수행할 수 있기 때문에 컴퓨터나 논리 회로 등에서 유용하게 이용된다.
2진법과 논리 연산[편집]
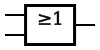
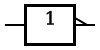
표기 숫자가 0과 1 두 가지밖에 없다는 특징 때문에 2진법은 참(True)과 거짓(False)을 나타내는 방식으로도 사용된다. 일반적으로 참(True)는 1로, 거짓(False)은 0으로 표시한다. 논리 연산은 몇 개의 2진수로 표기된 참과 거짓을 입력으로 받아들인 다음 특정한 방식의 연산을 수행하여 하나의 결과를 다시 참과 거짓을 의미하는 이진수 0 또는 1로 출력하는 것을 의미하며, 대표적인 연산으로는 AND, OR, NOT 연산 등이 있다. 아래의 그림은 AND, OR, NOT 연산의 표기와 진리표(Truth table)를 나타낸 것이다.
| 유형 | 논리 회로 표현 방식 | 논리 회로 표현 방식(직사각형) | 논리 연산 표기 방식 | 진리표(Truth table) | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AND | 
|

|
| |||||||||||||||||||
| OR | 
|
|
| |||||||||||||||||||
| NOT | 
|
|
| |||||||||||||||||||
이 외에도 NAND, NOR, XOR 회로 등 위의 세 논리 연산을 응용한 연산 방식들이 존재한다. 이와 같은 2진법에 근거한 논리 연산은 신호 전압이나 전류를 수치화된 논리 부호(참과 거짓)로 처리하는 디지털 회로(Digital circuit, 디지털 논리 회로)등에 유용하게 응용되고 있다.
10진법[편집]
10진법은 사람의 손가락이 10개인 것에서 유래한 만큼 현재 세계에서 가장 널리 쓰이고 있는 진법으로, 고대 이집트의 상형문자, 로마의 기수법, 중국의 기수법, 초기 인도 카로시의 기수법, 인도 브라미의 기수법 등 고대의 수많은 문화들이 10진법을 사용하였다고 한다. 고대 이집트의 상형문자는 크레타섬의 상형문자에 큰 영향을 끼쳤고, 이것은 다시 그리스의 청동기 시대의 수 체계 형성에도 영향을 끼쳤다. 10진법이 사용되는 곳은 셀 수 없이 많은데, 우리가 물건을 세거나, 계산을 하거나, 기초적인 수학문제를 푸는 등의 일상생활에서 사용하는 숫자들의 대부분이 10진법이다. 초기의 컴퓨터인 에니악, IBM 650 등에서도 2진법 대신 10진법을 사용하였으며, 현대의 컴퓨터에서도 사람에게 보이는 화면이나 사람에 의해 입력되는 부분의 상당수가 10진법으로 행해진다. 거리를 나타내는 단위인 킬로미터, 미터, 센티미터, 밀리미터, 무게의 단위인 킬로그램, 그램, 밀리그램, 시간의 단위인 초, 밀리초, 마이크로초 등등의 수많은 단위들도 모두 10진법을 바탕으로 한 단위들이다.
11진법[편집]
ISBN에서, 체크 디지트는 0,1,2,3,4,5,6,7,8,9,X를 사용하는 십일진법이다.
12진법[편집]

12진법은 1,2,3,4,6 등 약수를 많이 가지고 있기 때문에 과거 상거래에서 주요하게 사용되었으며, 현재에서 그 관습이 남아서 일부 단위에서 12진법이 사용되고 있다. 예를 들어 연필이나 펜을 세는 단위 다스는 12자루를 묶어서 나타내는 단위이며, 12다스는 다시 묶여서 1그로스라고 나타낸다. 로마인들은 화폐나 무게의 단위인 아스(As)라는 단위를 하부 단위인 12개의 온스(once)라고 나누어 사용하였고, 13세기까지 유럽인들도 화폐의 단위로서 투르(tournois)와 1/12 단위인 드니(denier)를 썼다. 12길이의 단위 중 하나인 1 피트(feet)는 12인치(inch)를 일컬으며, 프랑스 혁명 이전의 유럽인들은 12진법을 바탕으로 한 길이 단위를 사용하는 등 12진법은 길이의 표현에도 자주 사용되었다. 또한 한국과 중국 등 동양에서는 하루를 24시간으로 근거하여 동일하게 12개의 시간으로 나누었고, 수메르 인들도 하루를 12시간으로 나누어 1 단위를 '단나(Danna)'라고 하였다. 오늘날에도 오전과 오후가 각각 12시간으로 나뉘어 있으며, 1년도 12월로 구성되어 있는 등 시간 속에서 12진법을 확인할 수 있다. 이러한 12진법의 유용성 때문에 일부 학자들은 12진법이 10진법보다 더 우수한 기수법이라고 평가하기도 한다.[17]
60진법[편집]
60진법은 숫자를 표현하기에는 다소 복잡한 기수 체계이지만, 일부 민족들은 실제로 60진법을 사용하였다. 60진법을 처음 사용한 민족은 수메르 인으로, 그들이 어떠한 이유로 60진법을 사용하게 되었는지에 대한 기원은 아직까지도 학자들 사이에서 논쟁이 되고 있다. 이에 대해서는 엄지손가락을 제외한 네 손가락의 12마디에 비롯된 12진법과 10진법이 융합하여 두 수의 최소공배수인 60진법이 탄생하게 되었다는 것과 12진법에 나머지 손의 5개의 손가락에서 나온 5진법이 합해져 이들의 곱인 60진법이 생겨났다는 것 등 다양한 가설이 존재한다.[18]
현대의 문화에서도 60진법의 흔적을 찾을 수 있는데, 1시간은 60분으로 이루어져 있으며 1분은 다시 60초로 구성되어 있는 현대의 시간 체계는 60진법을 기초로 한 것이다. 이뿐만 아니라 기하학이나 천문학에서 사용되는 1도가 60분이고 1분이 60초인 각도 체계에서도 60진법을 확인할 수 있다.
진수[편집]
진법들의 숫자 또는 연산된 숫자를 진수 또는 진수값이라고 한다.
- 의 진법표기는 또는 또는 으로 표기한다. 이것의 진수값은 다음과 같이 구해진다.
- 의 진법표기는 또는 또는 으로 표기한다. 이것의 진수값은 다음과 같다.
- 의 진법표기는 또는 또는 으로 표기한다.
- 따라서 의 진법의 진수는 이므로,
- 따라서 의 진수는 이고,
- 의 진수는 이다.
이때, 지수법칙에 의해서,
진법간의 변환[편집]
- 진수은 아래와 같이 나머지 연산인에 의해 진법의 진수진수로 변환된다.
- 진수은 아래와 같이 진법의 진수진수로 변환된다.
소수[편집]
- 의 진수값은 다음과 같이 구해진다.
- 의 진수값은 다음과 같다.
각주[편집]
- ↑ 조르쥬 이프라(2002), 신비로운 수의 문화사, 예하, p. 23.
- ↑ 조르쥬 이프라(2002),신비로운 수의 역사, 예하, p. 266.(기원전 680-699년 앗시리아 왕 아자라돈의 <검은 돌>에서 발췌)
- ↑ 피터 S. 루드만(2009), 수학의 탄생(이집트부터 그리스까지 시대르 초월한 수학적 사고방식의 비밀을 추적하다), 살림MATH, p. 74.
- ↑ 카롤 A. 메닝거(2005), 수의 문화사, 열린책들, p. 379.
- ↑ 카롤 A. 메닝거(2005), 수의 문화사, 열린책들, p. 383.
- ↑ 조르쥬 이프라(2002),신비로운 수의 역사, 예하, p. 280.
- ↑ 조르쥬 이프라(2002),신비로운 수의 역사, 예하, p. 286.
- ↑ 조르쥬 이프라(2002),신비로운 수의 역사, 예하, p. 298.
- ↑ 조르쥬 이프라(2002),신비로운 수의 역사, 예하, p. 300-301.
- ↑ 조르쥬 이프라(2002),신비로운 수의 역사, 예하, p. 305.
- ↑ 조르쥬 이프라(2002),신비로운 수의 역사, 예하, p. 302.
- ↑ 조르쥬 이프라(2002),신비로운 수의 역사, 예하, p. 303-304.
- ↑ 김용운(2009), 한국 수학사(수학의 창을 통해 본 한국인의 사상과 문화), 살림MATH, p.513.
- ↑ 김용운(2009), 한국 수학사(수학의 창을 통해 본 한국인의 사상과 문화), 살림MATH, p.517.
- ↑ 현병주, 사개송도치부법, p.18.
- ↑ 네이버 백과사전, 2진법.http://100.naver.com/100.nhn?docid=128180
- ↑ 네이버 백과사전, 12진법.http://100.naver.com/100.nhn?docid=103457
- ↑ 조르쥬 이프라(2002), 신비로운 수의 역사, 예화, p 79-80.
같이 읽기[편집]
관련 서적[편집]
- 카롤 A. 메닝거(2005), 수의 문화사, 열린책들, ISBN 8932905894
- 조르쥬 이프라(2002), 신비로운 수의 역사, ISBN 8973854062
- 피터 S. 루드만(2009), 수학의 탄생(이집트부터 그리스까지 시대를 초월한 수학적 사고방식의 비밀을 추적하다), 살림MATH, ISBN 9788952210517
- 김용운(2009), 한국 수학사(수학의 창을 통해 본 한국인의 사상과 문화), 살림MATH, ISBN 9788952209399
외부 링크[편집]
- 고대의 기수법Archived 2012년 10월 22일 - 웨이백 머신
- 마야 문명의 기수법과 시간 체계 - Maya World Study Center
- 기수법 변환기












































































