수학적 최적화
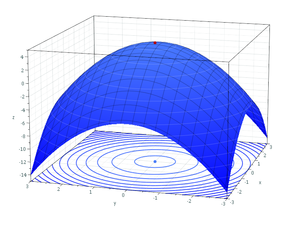
수학적 최적화(最適化, 영어: mathematical optimization 또는 mathematical programming)는 특정의 집합 위에서 정의된 실수값, 함수, 정수에 대해 그 값이 최대나 최소가 되는 상태를 해석하는 문제이다. 수리 계획 또는 수리 계획 문제라고도 한다. 물리학이나 컴퓨터에서의 최적화 문제는 생각하고 있는 함수를 모델로 한 시스템의 에너지를 나타낸 것으로 여김으로써 에너지 최소화 문제라고도 부른다.
최적화 문제[편집]
최적화 문제는 다음과 같은 방법으로 표현한다.
- 수식: 함수 f : A R 어떤 집합 A에서 실수 x 에 대해
- 의미: an elementx0 in A such that f(x0) ≤ f(x) for all x in A ("minimization") or such that f(x0) ≥ f(x) for all x in A ("maximization").
위와 같은 공식은 선형 계획법 (linear programming)이라 한다. 실생활 및 이론적 문제 모두가 이와 같은 보편적 방법으로 해결할 수 있다.
함수 f의 값이 최소이거나 최대인 값을 찾으면 최적화 해법(optimal solution)을 찾은 것이 된다.[1] 최적화 문제의 종류에 따라서 최적해를 찾기 위한 방법은 최소화(minimization) 혹은 최대화(maximization)로 나눌 수 있다.
역사[편집]
페르마와 라그랑주가 최적화를 정의하기 위한 미적분 기반 함수를 제시하였고, 뉴턴과 가우스는 최적화를 반복문을 통해 찾아가는 해법을 제시하였다. 역사적으로 최적화 분야에서 최초로 이름이 붙여진 용어는 선형 계획법이다.
계획법(programming)이라는 용어는 컴퓨터 프로그래밍(programming)과는 다른 용어이다. 미국에서 계획법이라는 용어는 조지 단치그의 연구 분야가 미국 육군에서 훈련과 수송 및 물류 업무에 활용되면서 널리 알려졌다.
주요 하위 분야[편집]
- convex / concave 계획법
- integer 계획법
- fraction 계획법
- 비선형 계획법
- stochastic 계획법
- stochastic 최적화
다중 객체 최적화 문제[편집]
이 문단은 비어 있습니다. 내용을 추가해 주세요. |
다중 해법 최적화 문제[편집]
다중 해법 최적화 문제(multi-modal optimization)은 여러 개의 해법을 가지는 최적화 문제이고 그 전부의 cost function이 동일하여 모두가 좋은 해법인 문제이다.
컴퓨터를 통한 최적화 기술[편집]
최적화 알고리즘[편집]
이 문단은 비어 있습니다. 내용을 추가해 주세요. |
반복 방법론[편집]
휴리스틱[편집]
이 문단은 비어 있습니다. 내용을 추가해 주세요. |
같이 보기[편집]
각주[편집]
| 이 글은 수학에 관한 토막글입니다. 여러분의 지식으로 알차게 문서를 완성해 갑시다. |



