몫공간

벡터 공간의 몫공간에 대해서는 몫 벡터 공간 문서를 참고하십시오.

일반위상수학에서 몫공간(-空間, 영어: quotient space)은 어떤 위상 공간의 몫집합 위에 표준적으로 존재하는 위상 공간이다.

정의

몫위상

위상 공간 $X$ 및 그 위의 동치 관계 ${\sim }\subseteq X^{2}$가 주어졌을 때, 몫집합 $X/{\mathord {\sim }}$ 위의 몫위상(-位相, 영어: quotient topology)은 다음 두 가지 방법을 통해 정의할 수 있으며, 이렇게 정의한 두 위상은 서로 같다.^:139

• (열린집합을 통한 정의) 부분 집합 $U\subseteq X/{\mathord {\sim }}$이 열린집합일 필요충분조건은 $[-]_{\sim }^{-1}(U)\subseteq X$가 $X$의 열린집합인 것이다. (여기서 $\textstyle [-]_{\sim }^{-1}(U)=\{x\in X\colon [x]_{\sim }\in U\}$는 $U$의 표준 사영 $X\to X/{\mathord {\sim }}$에 대한 원상이다.)
• (닫힌집합을 통한 정의) 부분 집합 $F\subseteq X/{\mathord {\sim }}$이 닫힌집합일 필요충분조건은 $[-]_{\sim }^{-1}(F)\subseteq X$가 $X$의 닫힌집합인 것이다.

이 위상은 표준 사영

$X\to X/{\mathord {\sim }}$

을 연속 함수로 만드는 가장 섬세한 위상이다. 또한, 이는 임의의 위상 공간 $Y$ 및 함수 $f\colon X/{\mathord {\sim }}\to Y$에 대하여 다음 두 조건을 동치로 만드는, 유일한 $X/{\mathord {\sim }}$ 위의 위상이다.

• $f$는 연속 함수이다.
• $f\circ [-]_{\sim }\colon X\to Y$는 연속 함수이다.

몫사상

두 위상 공간 $X$, $Y$ 사이의 전사 함수 $q\colon X\to Y$에 대하여, 다음 세 조건이 서로 동치이며, 이를 만족시키는 $q$를 몫사상(-寫像, 영어: quotient map)이라고 한다.^:137

• $f$는 연속 함수이며, 만약 $U\subseteq Y$가 부분 집합이며 $q^{-1}(U)\subseteq X$가 열린집합이라면, $U\subseteq Y$ 역시 열린집합이다.
• $f$는 연속 함수이며, 만약 $F\subseteq Y$가 부분 집합이며 $q^{-1}(F)\subseteq X$가 닫힌집합이라면, $F\subseteq Y$ 역시 닫힌집합이다.
• 임의의 위상 공간 $Z$ 및 함수 $f\colon Y\to Z$에 대하여, $f$가 연속 함수인 것과 $f\circ q\colon X\to Z$가 연속 함수인 것은 동치이다.

몫위상과 몫사상의 개념은 서로 동치이다. 구체적으로, 몫공간 $X/{\mathord {\sim }}$에 대하여, 표준 사영 $X\to X/{\mathord {\sim }}$은 몫사상이다. 반대로, 몫사상 $q\colon X\to Y$가 주어졌을 때, $X$ 위에 다음과 같은 동치 관계 ${\stackrel {q}{\sim }}$을 정의하자.

$x{\stackrel {q}{\sim }}x'\iff q(x)=q(x')\qquad \forall x,x'\in X$

그렇다면 $Y$는 몫공간 $X/{\mathord {\stackrel {q}{\sim }}}$과 위상 동형이다.

성질

함의 관계

모든 몫사상은 전사 연속 함수이며, 모든 열린 전사 연속 함수와 닫힌 전사 연속 함수는 몫사상이다. 몫사상이 단사 함수일 필요충분조건은 위상 동형 사상이다. 콤팩트 공간 $X$에서 하우스도르프 공간 $Y$로 가는 함수 $X\to Y$의 경우, 전사 연속 함수, 몫사상, 닫힌 전사 연속 함수의 개념이 서로 동치이다. (이는 모든 연속 함수 $X\to Y$가 닫힌 함수이기 때문이다.)

연산에 대한 닫힘

두 몫사상 $f\colon X\to Y$와 $g\colon Y\to Z$의 합성 $g\circ f\colon X\to Z$는 몫사상이다. 반대로, 만약 $f\colon X\to Y$와 $g\colon Y\to Z$가 연속 함수이며 $g\circ f$가 몫사상이라면, $f$ 역시 몫사상이다.

몫사상 $f\colon X\to Y$ 및 연속 함수 $h\colon X\to Z$에 대하여, 만약 $x,x'\in X$, $f(x)=f(x')$가 항상 $h(x)=h(x')$을 함의한다면, $f$와 $h$를 통해 유일하게 정의되는 함수

${\widetilde {h}}\colon Y\to Z$

${\widetilde {h}}\circ f=h$

는 연속 함수이다.^:142

몫사상 $q\colon X\to Y$ 및 부분 집합 $A\subseteq Y$에 대하여, 만약 다음 네 조건 가운데 하나가 성립한다면, 제한

$q\upharpoonright (q^{-1}(A),A)\colon q^{-1}(A)\to A$

는 몫사상이다.^:140

• $A\subseteq Y$는 열린집합이다.
• $A\subseteq Y$는 닫힌집합이다.
• $q$는 열린 함수이다.
• $q$는 닫힌 함수이다.

반대로, 만약 $q\colon X\to Y$가 전사 연속 함수이며, 임의의 $y\in Y$가 $q\upharpoonright (q^{-1}(N),N)$을 몫사상으로 만드는 근방 $N\ni y$를 갖는다면, $q$는 몫사상이다.

몫사상 $f\colon X\to Y$, $f'\colon X'\to Y'$에 대하여, 자연스럽게 정의되는 함수

$f\times f'\colon X\times X'\to Y\times Y'$

$f\times f'\colon (x,x')\mapsto (f(x),f'(x'))$

를 생각하자. 이는 전사 연속 함수이지만, (정의역과 공역의 곱위상에 대하여) 몫사상이 아닐 수 있다. 그러나 임의의 몫사상 $f\colon X\to Y$ 및 국소 콤팩트 공간 $Z$에 대하여,

$f\times \operatorname {id} _{Z}\colon X\times Z\to Y\times Z$

는 (곱위상에 대하여) 몫사상이다. 또한, 임의의 콤팩트 생성 공간 $X$, $Z$ 및 몫사상 $f\colon X\to Y$에 대하여,

$k(f\times \operatorname {id} _{Z})\colon k(X\times Z)\to k(Y\times Z)$

는 (콤팩트 생성 곱위상에 대하여) 몫사상이다.^{:192, Corollary 5.9.10}

끝 위상과의 관계

몫위상은 표준 사영에 대한 끝 위상이다. 반대로, 위상 공간 $Y$가 위상 공간들의 집합 $(X_{i})_{i\in I}$ 및 함수들의 집합 $(f_{i}\colon X_{i}\to Y)_{i\in I}$에 대한 끝 위상을 갖는다고 하자. 이는 위상합

$X=\bigsqcup _{i\in I}X_{i}$

위에 자연스럽게 유도되는 하나의 함수

$f\colon X\to Y$

에 대한 끝 위상과 같다. 이 경우, $f\upharpoonright (X,f(X))\colon X\to f(X)$는 몫사상이다. 따라서 $f(X)$는 열린닫힌집합이며, $X$의 몫공간과 위상 동형이다. 또한 $Y\setminus f(X)$은 이산 공간이다. 즉, $Y$는 $(X_{i})_{i\in I}$의 위상합의 몫공간과 이산 공간의 위상합이다.

예

다각형의 몫공간

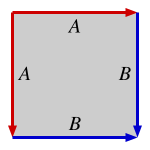
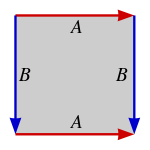
직사각형의 한 쌍의 대변을 직사각형의 둘레를 따라 회전하는 방향을 기준으로 반대 방향을 따라 붙여 몫공간을 취하면 원기둥을 얻으며, 같은 방향을 따라 붙이면 뫼비우스의 띠를 얻는다.

그림1	그림2	몫공간
		원기둥 ${\bar {\mathbb {D} }}^{2}\times [0,1]$
		뫼비우스의 띠 $\operatorname {M}$

만약 어떤 위상 공간이 변의 수가 짝수인 다각형의 변을 둘씩 짝을 지어 붙여 만든 몫공간과 위상 동형이라면, 이 다각형과 동치 관계의 순서쌍을 위상 공간의 다각형 표시(多角形表示, 영어: polygonal presentation)이라고 한다. 변의 수가 $2n$인 다각형 표현은 길이 $2n$의 문자열 $\alpha \in \{a_{1},a_{2},\dotsc ,a_{n},a_{1}^{-1},a_{2}^{-2},\dotsc ,a_{n}^{-1}\}^{2n}$로 나타낼 수 있다. 각 $i=1,2,\dotsc ,n$에 대하여, $\alpha$ 속에는 $a_{i}$가 정확히 두 번 등장하거나 $a_{i}$와 $a_{i}^{-1}$가 정확히 한 번씩 등장해야 한다. 만약 $\alpha _{i}=\alpha _{j}$라면, 다각형의 $i$번째 변과 $j$번째 변을 같은 방향으로 붙인다. 만약 $\alpha _{j}=\alpha _{i}^{-1}$라면, $i$번째 변과 $j$번째 변을 반대 방향으로 붙인다.

다각형 표시 그림	다각형 표시	몫공간 그림	몫공간
	$abb^{-1}a^{-1}$		구 $\mathbb {S} ^{2}$
	$abab$		실수 사영 평면 $\mathbb {RP} ^{2}$
	$abab^{-1}$		클라인 병 $\mathbb {RP} ^{2}\#\mathbb {RP} ^{2}$
	$aba^{-1}b^{-1}$		원환면 $\mathbb {T} ^{2}=\mathbb {S} ^{1}\times \mathbb {S} ^{1}$

부분 집합을 한 점으로 합친 공간

위상 공간 $X$의 부분 집합 $A$을 한 점으로 합쳐 만든 몫공간은

$X/A$

로 표기한다.

하우스도르프 공간 $X$ 및 콤팩트 집합 $A\subseteq X$에 대하여, $X/A$는 항상 하우스도르프 공간이다.

예를 들어,

$[0,1]/\{0,1\}\cong \mathbb {S} ^{1}$

${\bar {\mathbb {D} }}^{2}/\mathbb {S} ^{1}\cong \mathbb {S} ^{2}$

이다. 여기서 ${\bar {\mathbb {D} }}^{n}$은 $n$차원 유클리드 공간의 닫힌 공이며, $\mathbb {S} ^{n}$은 $n$차원 초구이다.

뿔

 이 부분의 본문은 붙임 공간입니다.

위상 공간 $X$ 위의 뿔은 다음과 같다.

$\operatorname {cone} (X)=(X\times [0,1])/(X\times \{0\})$

하우스도르프 공간 위의 뿔은 하우스도르프 공간이다.

유클리드 공간 $\mathbb {R} ^{n}$의 콤팩트 집합 $X$ 위의 뿔은 다음과 같은 공간과 위상 동형이다.

$\operatorname {cone} (X)\cong \{(1-t)a+tx\colon x\in X,\;t\in [0,1]\}$

$a\in \mathbb {R} ^{n+1}\setminus \mathbb {R} ^{n}$

임의의 연속 함수 $f\colon X\to Y$에 대하여, 다음 두 조건이 서로 동치이다.

• $f$는 널호모토픽하다.
• $f$의 연속 확장 $\operatorname {cone} (X)\to Y$이 존재한다.

붙임 공간

 이 부분의 본문은 붙임 공간입니다.

두 위상 공간 $X$, $Y$ 및 부분 집합 $A\subseteq X$ 및 연속 함수 $f\colon A\to Y$가 주어졌다고 하자. 위상합 $X\sqcup Y$ 위에 다음과 같은 동치 관계를 정의하자.

$x\sim f(x)\qquad \forall x\in A$

그렇다면, $f$의 붙임 공간은 다음과 같은 몫공간이다.

$Y\cup _{f}X=(X\sqcup Y)/\sim$

예를 들어,

${\bar {\mathbb {D} }}^{2}\cup _{\iota _{\mathbb {S} ^{1}}}{\bar {\mathbb {D} }}^{2}\cong \mathbb {S} ^{2}$

$\operatorname {M} \cup _{\iota _{\partial {\operatorname {M} }}}\operatorname {M} \cong \mathbb {RP} ^{2}\#\mathbb {RP} ^{2}$

$M\cup _{f}{\bar {\mathbb {D} }}^{2}\cong \mathbb {RP} ^{2}$

이다. 여기서 $\iota _{\mathbb {S} ^{1}}\colon \mathbb {S} ^{1}\to {\bar {\mathbb {D} }}^{2}$와 $\iota _{\partial {\operatorname {M} }}\colon \partial {\operatorname {M} }\to \operatorname {M}$은 포함 함수이며, $f\colon \partial {\bar {\mathbb {D} }}^{2}\to \partial {\operatorname {M} }$는 두 경계 사이의 위상동형사상이다.

열린 함수나 닫힌 함수가 아닌 몫사상

몫공간 $\mathbb {R} /(0,1]$으로의 표준 사영 $p\colon \mathbb {R} \to \mathbb {R} /(0,1]$은 몫사상이지만, 열린 함수가 아니며 닫힌 함수도 아니다. 예를 들어, $(-\infty ,1)\subseteq \mathbb {R}$는 열린집합이지만, $p((-\infty ,1))\subseteq \mathbb {R} /(0,1]$은 열린집합이 아니다. 이는

$p^{-1}(p((-\infty ,1)))=(-\infty ,1]\subseteq \mathbb {R}$

가 열린집합이 아니기 때문이다. 또한 $[1,\infty )\subseteq \mathbb {R}$는 닫힌집합이지만, $p([1,\infty ))\subseteq \mathbb {R} /(0,1]$은 닫힌집합이 아니다. 이는

$p^{-1}(p([1,\infty )))=(0,\infty )\subseteq \mathbb {R}$

가 닫힌집합이 아니기 때문이다.

곱이 몫사상이 아닌 두 몫사상

몫공간 $\mathbb {Q} /\mathbb {Z}$로의 표준 사영 $\mathbb {Q} \to \mathbb {Q} /\mathbb {Z}$과 항등 함수 $\mathbb {Q} \to \mathbb {Q}$의 곱

$f\colon \mathbb {Q} \times \mathbb {Q} \to \mathbb {Q} /\mathbb {Z} \times \mathbb {Q}$

는 (곱위상에 대하여) 몫사상이 아니다. 예를 들어, 임의의 $n\in \mathbb {Z}$에 대하여 $r_{n}={\sqrt {2}}/(|n|+1)$이라고 하자. 또한 $A_{n}\subseteq [n,n+1]\times \mathbb {R}$가 $(n,r_{n})$, $(n+1/2,r_{n})$, $(n+1,r_{n+1})$을 꼭짓점으로 하는 열린 삼각형 영역이라고 하고,

$B=(\mathbb {Q} \times \mathbb {Q} )\cap \operatorname {cl} _{\mathbb {R} ^{2}}\bigcup _{n\in \mathbb {Z} }A_{n}$

라고 하자. 그렇다면,

$f^{-1}(f(B))=B\subseteq \mathbb {Q} \times \mathbb {Q}$

는 닫힌집합이지만, $f(B)\subseteq \mathbb {Q} /\mathbb {Z} \times \mathbb {Q}$는 닫힌집합이 아니다. 이는

$f((0,0))\in \operatorname {cl} _{\mathbb {Q} /\mathbb {Z} \times \mathbb {Q} }f(B)\setminus f(B)$

이기 때문이다.

외부 링크

• “Quotient space” (영어). 《Encyclopedia of Mathematics》. Springer-Verlag. 2001. ISBN 978-1-55608-010-4. 
• “Quotient mapping” (영어). 《Encyclopedia of Mathematics》. Springer-Verlag. 2001. ISBN 978-1-55608-010-4. 
• Weisstein, Eric Wolfgang. “Quotient space” (영어). 《Wolfram MathWorld》. Wolfram Research. 
• “Quotient space” (영어). 《nLab》. 
• “Quotient topology” (영어). 《Topospaces》. 
• “Quotient map” (영어). 《Topospaces》. 
• “Quotient space” (영어). 《PlanetMath》. 
• “Definition:Quotient topology” (영어). 《ProofWiki》.