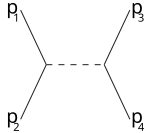
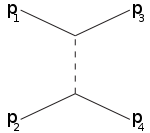
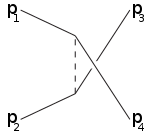
산란 이론에서, 만델스탐 변수 (영어 : Mandelstam variable )는 두 입자 가 산란하여 튕겨나오는 과정에서, 각 입자의 초기 4차원 운동량과 나중 4차원 운동량의 관계를 나타내는 세 변수 s , t , u 다. 단위는 에너지의 제곱. 남아공 의 물리학자 스탠리 만델스탐 (Stanley Mandelstam)이 도입하였다.[1]
+−−− 계량 부호수 를 사용하자. 사차원 운동량 이 각각
p
1
{\displaystyle p_{1}}
p
2
{\displaystyle p_{2}}
p
3
{\displaystyle p_{3}}
p
4
{\displaystyle p_{4}}
사차원 운동량 을 가지게 된다고 하자. 그렇다면 만델스탐 변수
s
{\displaystyle s}
t
{\displaystyle t}
u
{\displaystyle u}
s
=
(
p
1
+
p
2
)
2
=
(
p
3
+
p
4
)
2
{\displaystyle s=(p_{1}+p_{2})^{2}=(p_{3}+p_{4})^{2}}
t
=
(
p
1
−
p
3
)
2
=
(
p
2
−
p
4
)
2
{\displaystyle t=(p_{1}-p_{3})^{2}=(p_{2}-p_{4})^{2}}
u
=
(
p
1
−
p
4
)
2
=
(
p
2
−
p
3
)
2
{\displaystyle u=(p_{1}-p_{4})^{2}=(p_{2}-p_{3})^{2}}
여기서 s 는 무게중심 기준틀 에서 관측한 에너지 의 제곱과 같다. t 는 한 입자에서 다른 입자로 옮겨간 운동량 의 정도(의 제곱)으로 해석할 수 있다.
세 만델스탐 변수들은 서로 독립적이지 않으며, 다음과 같은 관계를 만족시킨다.
s
+
t
+
u
=
m
1
2
+
m
2
2
+
m
3
2
+
m
4
2
{\displaystyle s+t+u=m_{1}^{2}+m_{2}^{2}+m_{3}^{2}+m_{4}^{2}}
여기서
m
i
2
=
p
i
2
{\displaystyle m_{i}^{2}=p_{i}^{2}}
불변 질량 이다.
만약 산란 뒤 입자가 산란 이전 입자와 다를 경우, 서로 유사한 입자의 운동량을
p
1
{\displaystyle p_{1}}
p
3
{\displaystyle p_{3}}
p
2
{\displaystyle p_{2}}
p
4
{\displaystyle p_{4}}
e+ +e−
→
{\displaystyle \to }
+ +μ− 와 같은 경우, 전자 (e− )와 뮤온 (μ− )이 서로 유사하므로 이들을 각각
p
1
{\displaystyle p_{1}}
p
3
{\displaystyle p_{3}}
파인먼 도형의 모양 [ 편집 ] 이 세 변수에 비례하는 산란 진폭 성분을 나타내는 파인먼 도형 은 다음과 같이 특정한 모양을 지닌다. 이런 모양의 파인먼 도형에 해당하는 산란 진폭 성분을 s 채널 · t 채널 · u 채널 로 부른다.
s
{\displaystyle s}
t
{\displaystyle t}
u
{\displaystyle u}
임의의 차원에서의 만델스탐 변수 [ 편집 ] 일반적으로,
D
{\displaystyle D}
N
>
2
{\displaystyle N>2}
p
1
,
…
,
p
N
{\displaystyle p_{1},\dots ,p_{N}}
만델스탐 변수
s
i
j
{\displaystyle s_{ij}}
s
i
j
=
(
p
i
+
p
j
)
2
(
1
≤
i
<
j
≤
N
)
{\displaystyle s_{ij}=(p_{i}+p_{j})^{2}\qquad (1\leq i<j\leq N)}
즉, 총
N
(
N
−
1
)
/
2
{\displaystyle N(N-1)/2}
∑
j
≠
i
s
i
j
=
∑
j
=
1
N
m
j
2
+
(
N
−
4
)
m
i
2
{\displaystyle \sum _{j\neq i}s_{ij}=\sum _{j=1}^{N}m_{j}^{2}+(N-4)m_{i}^{2}}
4차원에서는
s
=
s
12
{\displaystyle s=s_{12}}
t
=
s
13
{\displaystyle t=s_{13}}
u
=
s
14
{\displaystyle u=s_{14}}
이므로, 이 상관관계는 4차원에서의 상관관계
s
+
t
+
u
=
∑
i
=
1
4
m
i
2
{\displaystyle s+t+u=\sum _{i=1}^{4}m_{i}^{2}}
의 일반화이다.
독립 만델스탐 변수들의 수 [ 편집 ] 편의상
D
′
=
D
−
min
{
N
,
D
}
{\displaystyle D'=D-\min\{N,D\}}
로 정의하자. 운동량들 사이에는 다음과 같은 조건들이 존재한다.
(질량껍질 조건)
p
i
2
=
m
i
2
∀
i
=
1
,
…
,
N
{\displaystyle p_{i}^{2}=m_{i}^{2}\;\forall i=1,\dots ,N}
(운동량 보존 법칙 )
∑
i
=
1
N
p
i
=
0
{\displaystyle \sum _{i=1}^{N}p_{i}=0}
또한, 로런츠 변환 을 통해
D
(
D
−
1
)
/
2
{\displaystyle D(D-1)/2}
개의 추가 제약을 가할 수 있으나, 이들 가운데
D
′
(
D
′
−
1
)
/
2
{\displaystyle D'(D'-1)/2}
개는 자명하게 작용 한다. 따라서, 독립적인 만델스탐 변수의 개수는
N
D
−
N
−
D
+
D
′
−
D
(
D
−
1
)
/
2
+
D
′
(
D
′
−
1
)
/
2
=
{
N
(
D
−
1
)
−
D
(
D
+
1
)
/
2
D
≤
N
N
(
N
−
3
)
/
2
D
−
1
≥
N
{\displaystyle ND-N-D+D'-D(D-1)/2+D'(D'-1)/2={\begin{cases}N(D-1)-D(D+1)/2&D\leq N\\N(N-3)/2&D-1\geq N\end{cases}}}
이다.
다양한 차원에서 독립 만델스탐 변수들의 수
입자 수 N
D = 2D = 3D = 4D = 5D = 6
3
0
0
0
0
0
4
1
2
2
2
2
5
2
4
5
5
5
6
3
6
8
9
9
2차원 만델스탐 변수 [ 편집 ] 2차원에서는 2→2 산란 과정에서 오직 하나만의 독립적 만델스탐 변수가 존재하며, 이는 신속도 로 쓸 수 있다.
네 입자의 신속도를 각각
θ
1
{\displaystyle \theta _{1}}
θ
2
{\displaystyle \theta _{2}}
θ
3
{\displaystyle \theta _{3}}
θ
4
{\displaystyle \theta _{4}}
p
i
=
m
i
(
cosh
θ
i
,
sinh
θ
i
)
{\displaystyle p_{i}=m_{i}(\cosh \theta _{i},\sinh \theta _{i})}
이다.
편의상 모든 입자의 질량이
m
1
=
m
2
=
m
3
=
m
4
=
m
{\displaystyle m_{1}=m_{2}=m_{3}=m_{4}=m}
로런츠 변환 을 가해
θ
1
+
θ
2
=
0
{\displaystyle \theta _{1}+\theta _{2}=0}
θ
3
+
θ
4
=
0
{\displaystyle \theta _{3}+\theta _{4}=0}
으로 놓자. 그렇다면 운동량 보존에 따라서
θ
1
=
−
θ
2
=
±
θ
3
=
∓
θ
4
{\displaystyle \theta _{1}=-\theta _{2}=\pm \theta _{3}=\mp \theta _{4}}
임을 알 수 있다.
2
θ
=
θ
1
−
θ
2
=
±
(
θ
3
−
θ
4
)
{\displaystyle 2\theta =\theta _{1}-\theta _{2}=\pm (\theta _{3}-\theta _{4})}
로 놓자. 그렇다면
s
=
4
m
2
cosh
2
θ
{\displaystyle s=4m^{2}\cosh ^{2}\theta }
t
=
−
m
2
(
1
∓
1
)
2
sinh
2
θ
{\displaystyle t=-m^{2}(1\mp 1)^{2}\sinh ^{2}\theta }
u
=
−
m
2
(
1
±
1
)
2
sinh
2
θ
{\displaystyle u=-m^{2}(1\pm 1)^{2}\sinh ^{2}\theta }
이 된다 (복호 동순).
참고 문헌 [ 편집 ]