파인만 도형
 | |
| 대칭 | |
|---|---|
| 시공간 | 병진 대칭 · 로런츠 군 · 푸앵카레 군 · 등각 대칭 |
| 이산 대칭 | 전하 켤레 대칭 (C) · 반전성 (P) · 시간 역전 대칭 (T) |
| 기타 | 게이지 이론 · 초대칭 |
| 대칭 깨짐 | 자발 대칭 깨짐 · 골드스톤 보손 · 힉스 메커니즘 · 변칙 |
| 도구 | |
| 기본 개념 | 전파 인자 · 윅 정리 (표준 순서) · LSZ 축약 공식 · 상관 함수 |
| 양자화 | 정준 양자화 · 경로 적분 |
| 산란 이론 | 산란 행렬 · 만델스탐 변수 |
| 섭동 이론 | 파인만 도형 · 질량껍질 · 가상 입자 |
| 조절과 재규격화 | 파울리-빌라르 조절 · 차원 조절 · 최소뺄셈방식 · 재규격화군 · 유효 이론 (유효 작용) |
| 게이지 이론 | 공변미분 · 파데예프-포포프 유령 · BRST 대칭 · 워드-다카하시 항등식 |
| 이론 | |
| 장난감 모형 | 사승 상호작용 · 콜먼-와인버그 모형 · 시그마 모형 · 베스-추미노 모형 |
| 게이지 이론 | 양자 전기역학 · 양-밀스 이론 · 양자 색역학 · 전기·약 이론 · 표준 모형 |
| 대통일 이론 | 대통일 이론 · 페체이-퀸 이론 · 시소 메커니즘 · 최소 초대칭 표준 모형 · 테크니컬러 |
| 학자 | |
| 초기 학자 | 위그너 · 마요라나 · 바일 |
| 전자기력 | 디랙 · 슈윙거 · 도모나가 · 파인만 · 다이슨 |
| 강한 상호작용 | 유카와 · 겔만 · 그로스 · 폴리처 · 윌첵 |
| 약한 상호작용 | 양전닝 · 리정다오 · 난부 · 글래쇼 · 살람 · 와인버그 · 고바야시 · 마스카와 · 힉스 · 앙글레르 |
| 재규격화 | 펠트만 · 엇호프트 · 윌슨 |
양자장론에서 파인만 도형(Feynman diagram)은 양자장 혹은 통계물리의 장에서 전이진폭 혹은 상관함수의 계산에서 나타나는 항들을 나타내는 도형이다. 리처드 파인만이 도입하였으며, 그의 이름을 따라 명명되었다.
양자장론의 정준 수식화에서 파인만 도형은 산란행렬의 윅의 정리에 따른 섭동이론적 전개에서의 특정 항을 나타낸다. 이때 전이진폭은 양자계의 시작과 끝 사이의 상태에 대한 산란행렬의 성분이다. 경로적분의 관점에서 보면, 전이진폭은 계의 처음과 마지막 상태 사이의 모든 가능한 경로들의 (가중된) 합이다. 파인먼 도형은 성분이 결합하고 쪼개어지는 그림을 통해 입자의 특정 경로를 직관적으로 나타낸다.
파인만 도형의 규칙[편집]
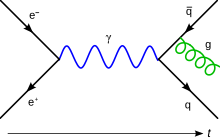
파인만 도형은 일종의 그래프로, 다음과 같은 규칙을 따른다.
- 입자의 전파인자는 변으로, 입자 사이의 상호작용은 꼭짓점으로 나타낸다.
- 입자가 그 반입자와 다를 경우 (디랙 페르미온, 복소 스칼라 입자, W보손 등), 그 변은 유향(directed)변이다. 즉, 변에다 작은 화살표로 방향을 표시한다. 입자의 경우는 초기 상태에서 최종 상태를 향하여, 반입자의 경우 최종 상태에서 초기 상태를 가리킨다.
- 입자가 그 반입자와 같은 경우 (광자, Z보손, 실수 스칼라 입자 등), 화살표를 표시하지 않는다.
- 광자와 W와 Z보손은 물결선(〰)으로 나타낸다. 글루온은 꼬인 선(➿)으로 나타낸다. 기타 입자를 구별할 필요가 있으면 변 옆에 부호로 표시한다.
역사[편집]
리처드 파인만이 1948년에 도입하였으나, 출판하지 않았다. 출판물에서는 프리먼 다이슨이 1949년에 최초로 사용하였다.[1]
참고 문헌[편집]
- Smirnov, Vladimir Alexandrovich (2009). “Multiloop Feynman integrals”. 《Scholarpedia》 4 (6): 8507. doi:10.4249/scholarpedia.8507.
- Veltman, Martinus (1994년 6월). 《Diagrammatica: The Path to Feynman Diagrams》. Bibcode:1994diag.book.....V. doi:10.1017/CBO9780511564079. ISBN 9780521456920.
- Kaiser, David (2005년 6월). 《Drawing Theories Apart: The Dispersion of Feynman Diagrams in Postwar Physics》. University of Chicago Press. ISBN 9780226422664.
- Polyak, Michael (2005). “Feynman diagrams for pedestrians and mathematicians”. 《Proceedings of Symposia in Pure Mathematics》 73: 15-42. arXiv:math/0406251. Bibcode:2004math......6251P.
외부 링크[편집]
 |
위키미디어 공용에 관련된 미디어 분류가 있습니다. |
- SLAC의 파인만 도형 소개
- 위키 문헌에서 파인만 도형을 바로 작성할 수 있게 해주는 WikiTeX 지원 안내문서.
- FeynDiagram으로 파인만 도형 그리기 : 포스트스크립트 출력용 C++ 라이브러리.
- Thorsten Ohl의 Feynmf LaTeX 패키지를 사용한 파인만 도형 예제.
- JaxoDraw : 파인만 도형을 그리는 자바 프로그램.
각주[편집]
- ↑ Dyson, Freeman J. (1949). “The Radiation Theories of Tomonaga, Schwinger, and Feynman” (PDF). 《Physical Review》 75 (3): 486–502. Bibcode:1949PhRv...75..486D. doi:10.1103/PhysRev.75.486.
|
이 글은 물리학에 관한 토막글입니다. 여러분의 지식으로 알차게 문서를 완성해 갑시다. |