위키백과, 우리 모두의 백과사전.
|
|
이 문서의 내용은 출처가 분명하지 않습니다.
지금 바로 이 문서를 편집하여, 참고하신 문헌이나 신뢰할 수 있는 출처를 주석 등으로 표기해 주세요. 검증되지 않은 내용은 삭제될 수도 있습니다. 내용에 대한 의견은 토론 문서에서 나누어 주세요. |
산란(散亂) 또는 흩뜨림은 어떤 매질을 직선 경로로 통과하는 빛, 소리, 움직이는 입자 등의 복사(輻射)가 하나 이상의 국부적 불균일성에 의해 경로를 벗어나는 현상을 가리키는 일반적인 물리적인 과정이다. 일반적으로는 반사의 법칙으로 예측한 경로가 아닌 방향으로 반사되는 복사를 일컫는다. 산란되는 반사를 보통 '난반사'라고 부르며, 산란되지 않는 반사를 '정반사'(또는 거울반사)라고 부른다.
산란을 일으키는 불균일성 입자를 '산란자'(scatterer) 또는 '산란중심'(scattering center)이라고 한다. 그 종류는 일일이 나열할 수 없을 정도로 많지만 몇 가지 예를 들어보자면, 미립자, 기포, 물방울, 유체의 밀도 변동, 다결정고체의 결정, 단결정고체의 흠집, 거친 표면, 유기체의 세포, 천의 직물성 섬유 등이다. 모든 전파되거나 이동하는 입자의 경로에 대한 이러한 특징의 효과는 산란 이론의 기초에서 다뤄진다.
산란과 산란 이론을 중요하게 여기는 분야에는 레이더 감지, 의료 초음파, 반도체 웨이퍼 검사, 중합 과정 모니터링, 자유공간 통신, CGI 등이 있다.
단일 산란과 다중 산란[편집]
산란 이론[편집]
전자기 산란[편집]
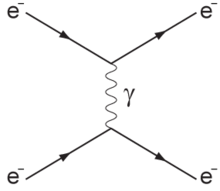
전자기파는 산란이 일어나는 복사의 형태로서 잘 알려져 있으며 가장 흔하게 접할 수 있다. 빛과 전파(특히 레이더)의 산란은 특히 중요하다. 전자기파 산란의 몇 가지 다양한 측면은 관습적인 명칭을 가질 수 있을 만큼 뚜렷하다. 탄성 빛 산란의 대표적인 형태는 레일리 산란과 미 산란이다. 비탄성 산란에는 브릴루앙 산란과 라만 산란, 비탄성 X-ray 산란과 콤프턴 산란이 포함된다.
같이 보기[편집]
바깥 고리[편집]
불교에서의 산란(散亂)에 대해서는 산란 (마음작용) 문서를 참조하십시오.
이 부분은 토막글입니다. 서로 지식을 모아 알차게 문서를 완성해 갑시다.
