쌍곡 좌표계

오일러 평면에 나타낸 쌍곡 좌표계: 같은 파란색 직선에 있는 모든 점은 같은 좌표값 u를 공유하고, 같은 빨간색 쌍곡선에 있는 모든 점은 같은 좌표값 v를 공유한다.

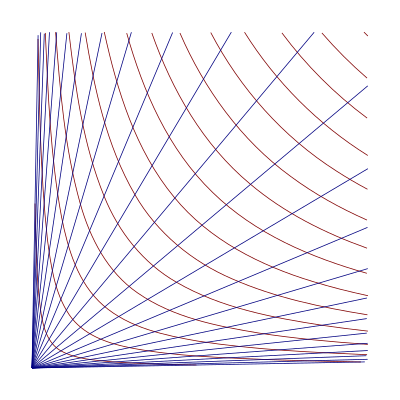
수학에서 쌍곡 좌표계(영어: hyperbolic coordinates)는 데카르트 좌표 평면의 제 1사분면에 있는 점들을 위치시키는 방법이다.

$\{(x,y)\ :\ x>0,\ y>0\ \}=Q$.

쌍곡 좌표계는 다음과 같이 정의된 쌍곡면의 값을 가진다:

$HP=\{(u,v):u\in \mathbb {R} ,v>0\}$.

HP에 있는 이 좌표계는 Q에 있는 정비례의 로그 비교 연구와 정비례의 편차 측정 연구에서 유용하다.

$Q$에 있는 $(x,y)$에 대해서 u와 v는 다음과 같다:

$u=\ln {\sqrt {\frac {x}{y}}}$

$v={\sqrt {xy}}$

매개변수 u는 (x, y)의 쌍곡선각이고 v는 x와 y의 기하 평균이다.

역 변환은 다음과 같다:

$x=ve^{u},\quad y=ve^{-u}$.

함수 $Q\rightarrow HP$는 연속 함수지만 해석 함수는 아니다.

다른 사분면 측도

HP는 쌍곡 기하학의 푸앵카레 반평면 모델의 측도 공간 구조를 가져오기 때문에, 전단사 대응 $Q\leftrightarrow HP$는 이 구조를 Q로 가져온다. 쌍곡 이동의 표기법을 통해서 쓸 수 있다. HP에 있는 측지선은 경계를 중심으로 하는 반원이기 때문에, Q에 있는 측지선은 대응점에서 얻을 수 있고 윈점에서 출발하는 반직선이나 원점에서 떠나고 원점으로 재진입하는 꽃잎 모양의 곡선으로 바뀐다. 좌우 이동으로 주어진 HP의 쌍곡 이동은 Q에 누름 변환을 적용시킨 것에 대응한다.

Q에 있는 쌍곡선은 HP의 경계에 평행한 직선에 대응하기 때문에, Q의 측도 기하학에서는 호로사이클(영어: horocycle)이다.

평면의 유클리드 위상과 Q를 상속받은 위상만을 고려하면, Q에 제한된 직선은 Q에 가까워 보인다. 측도 공간 HP에서 보면 열린 집합 Q가 경계로 대응하는 원점을 유일하게 가진다는 것을 나타낸다. 실제로 HP의 경계 R과 수직인 반직선인 Q의 원점에서 나가는 반직선과 그 이미지를 생각하라. HP에 있는 어떤 점이든지 R의 수직선의 최하부에 있는 점 p에 대해서 무한한 거리를 가지지만, 이 수직선에 있는 점의 수열은 p의 방향으로 나아가는 경향이 있을 수 있다. Q에 있는 대응하는 수열은 원점을 향하는 반직선을 따르는 경향이 있다. Q의 고전 유클리드 경계는 더 이상 관련이 없다.

물리학의 적용

기본 물리학적 변수는 종종 k = x y의 형태의 방정식에 관여된다. 예를 들면, V = I R (옴의 법칙), P = V I (전력), P V = k T (이상기체 법칙), 그리고 f λ = v (파동에서 파장, 주파수, 그리고 속도의 관계)가 있다. k가 상수일 경우, 다른 변수는 적절한 Q 사분면의 호로사이클인 쌍곡선에 있다.

예를 들어, 열역학에서 등온과정은 명시적으로 쌍곡선 궤적을 따르고 일은 쌍곡선각의 변화로 해석할 수 있다. 비슷하게, 부피가 변하는 기체의 질량 M이 주어졌을 때 밀도 δ = M / V이고, 이상기체 법칙은 P = k T δ로 쓸 수 있어서 등적과정 궤적은 절대온도와 기체 밀도의 사분면의 쌍곡선이다.

상대성 이론에서의 쌍곡 좌표계에 대해서는 역사 문단을 참고하라.

통계적 적용

• 사분면에서 인구 밀도의 비교 연구는 참조 국가, 지역, 또는 도시 영역의 인구와 면적을 점 (1,1)로 설정하는 것에서 시작한다.
• 간접 민주제인 지역의 선출된 대표의 분석은 비교를 위한 표준을 설정하는 것이다: 규모와 (대리인의) 슬레이트 규모가 사분면의 (1,1)에 있는 특정 대표 그룹이다.

경제학적 적용

경제학에서 쌍곡 좌표계의 필연적인 적용이 있다:

• 통화 환율 변동의 해석:

단위 통화를 $x=1$로 둔다. 가격 통화는 $y$에 대응한다. $0<y<1$일 때, 양의 쌍곡선각 $u>0$를 찾는다. 변동에 대해서 사로운 가격을 잡는다:

$0<z<y$.

그러면 u의 변화는 다음과 같다:

$\Delta u=\ln {\sqrt {\frac {y}{z}}}$.

환율 변동을 쌍곡선각으로 정량화하는 것은 객관적이고 대팅적이며 일관적인 측도를 제공한다. $\Delta u$는 통화 변동의 쌍곡 이동의 수평 이동 거리이다.

• 장바구니 가격의 인플레이션이나 디플레이션의 해석.
• 복점에서 시장점유율의 변화의 정량화.
• 회사 주식 분할 대 자사주매입.

역사

The 기하 평균은 오래된 개념이지만 쌍곡선각이 이 개념에서 그레고이르 드 세인트 빈센트(G. de Saint-Vincent)에 의해 만들어졌다. 그는 직각 쌍곡선 y = 1/x에 대해서 구적법을 하려고 시도하던 중이였다. 이 문제는 아르키메데스가 포물선의 구적법을 풀기 전 까지는 미해결 문제로 남아있었다. 단위 정사각형에서 원점의 반대쪽에 있는 (1,1)을 지난다. 곡선의 다른 점은 이 정사각형과 면적이 같은 직사각형으로 볼 수 있다. 이런 직사각형은 정사각형에 누름 변환을 가해서 얻을 수 있다. 이런 변환을 보기 위한 방법은 쌍곡선 영역을 통한 것이다. 레온하르트 오일러의 Introduction to the Analysis of the Infinite (1748)에 따라 단위 면적의 쌍곡선 영역은 (1,1)에서 시작해서 (e, 1/e)에서 끝나고, 이 때 e는 2.71828...이다.

(e, 1/e)을 단위 면적을 가지는 직사각형의 꼭짓점으로 두고, 단위 정사각형을 그 사각형으로 만드는 누름 변환을 다시 적용 시키면 $(e^{2},\ e^{-2})$을 얻는다. 일반적으로 누름 변환을 n번 적용하면 $(e^{n},\ e^{-n})$을 얻는다. 알퐁스 안토니오 드 사라사(A. A. de Sarasa)는 그레고이르 드 세인트 빈센트의 발견과 유사하게 기하수열에서 가로 좌표가 늘어남에 따라 쌍곡선의 면적의 합은 등차수열로 증가하고, 이 특성은 곱셈을 덧셈으로 줄여주는 로그에 대응한다는 발견을 했다. 오일러의 작업은 자연로그를 표준 수학적 도구로, 그리고 고등 수학을 초월 함수의 영역으로 만들었다. 쌍곡 좌표계는 쌍곡선의 구적법을 제공하고 대수함수의 한계를 초월한 그레고이르 드 세인트 빈센트의 원본 그림을 기반으로 한다.

특수 상대성이론에서 관심은 주어진 고유시간 이후에 다양한 속도로 도달할 수 있는 미래 시공간의 3차원 초표면에 있다. 월터 스콧 은 1907년 11월에 헤르만 민코프스키가 Göttingen Mathematical Society에서 이야기 하던 중에 사차원이 아니라 잘 알려진 삼차원 쌍곡 기하학을 언급했다고 설명한다. 표준 입문 우주단위 상대성 이론에 대한 교과서의 저자인 볼프강 린들러에 대한 경의를 표하며, 시공간의 쌍곡 좌표계는 린들러 좌표계라고 부른다.

참고 문헌

• David Betounes (2001) Differential Equations: Theory and Applications, page 254, Springer-TELOS, ISBN 0-387-95140-7 .
• Scott Walter (1999). "The non-Euclidean style of Minkowskian relativity" Archived 2013년 10월 16일 - 웨이백 머신. Chapter 4 in: Jeremy J. Gray (ed.), The Symbolic Universe: Geometry and Physics 1890-1930, pp. 91–127. Oxford University Press. ISBN 0-19-850088-2.