푸아송 분포

푸아송 분포

확률 질량 함수
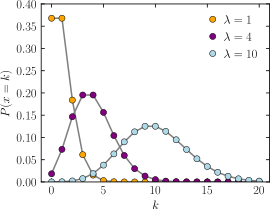
누적 분포 함수
기호	$\mathrm {Pois} (\lambda )$, $\mathrm {Poisson} (\lambda )$
매개변수	$\lambda >0$
지지집합	0 이상의 정수
확률 질량	${\frac {\lambda ^{k}}{k!}}\cdot e^{-\lambda }$
누적 분포	$e^{-\lambda }\sum _{i=0}^{\lfloor k\rfloor }{\frac {\lambda ^{i}}{i!}}={\frac {\Gamma (\lfloor k+1\rfloor ,\lambda )}{\lfloor k\rfloor !}}$ (이때 $\Gamma (x,y)$는 불완전 감마 함수, $\lfloor x\rfloor$는 바닥 함수)
기댓값	$\lambda$
최빈값	$\lceil \lambda \rceil -1$
분산	$\lambda$
비대칭도	$\lambda ^{-1/2}\,$
적률생성함수	$\exp(\lambda (e^{t}-1))\,$
특성함수	$\exp(\lambda (e^{it}-1))\,$

푸아송 분포(Poisson分布, 영어: Poisson distribution)는 확률론에서 단위 시간 안에 어떤 사건이 몇 번 발생할 것인지를 표현하는 이산 확률 분포이다. 단위 시간 대신 다른 단위(가령, 공장의 생산량 묶음 단위인 로트(lot) 등)를 사용할 수 있다. 이때 일어날 확률은 일정하고, 매우 작아야 한다.

역사

19세기에 시메옹 드니 푸아송이 1838년 저서 《민사 사건과 형사 사건 재판에서의 확률에 관한 연구 및 일반적인 확률 계산 법칙에 대한 서문》(프랑스어: Probabilité des jugements en matière criminelle et en matière civile, précédées des règles générales du calcul des probabilitiés)에서 최초로 사용하였다.

정의

정해진 시간 안에 어떤 사건이 일어날 횟수에 대한 기댓값을 $\lambda$라고 했을 때, 그 사건이 $k$회 일어날 확률은 다음과 같다.

$f(k;\lambda )={\frac {\lambda ^{k}e^{-\lambda }}{k!}},\,\!$

여기서 $e$는 자연상수이다.

특성

1. 어떤 단위구간(예, 1일)동안 이를 더 짧은 작은 단위의 구간(예: 1시간)로 나눌 수 있고 이러한 더 짧은 단위구간 중에 어떤 사건이 발생할 확률은 전체 척도 중에서 항상 일정해야 한다.
2. 두 개 이상의 사건이 동시에 발생할 확률은 0에 가깝다.
3. 어떤 단위구간의 사건의 발생은 다른 단위구간의 발생으로부터 독립적이다.
4. 특정 구간에서의 사건 발생확률은 그 구간의 크기에 비례한다.
5. 푸아송분포 확률 변수의 기댓값과 분산은 모두 λ이다.

응용

다음과 같은 확률적인 문제를 알아내기 위해 쓰이고 있다.

• 주어진 일정 시간 동안에 도착한 고객의 수
• 1킬로미터 도로에 있는 흠집의 수
• 주어진 일정 생산시간 동안 발생하는 불량 수
• 하룻동안 발생하는 출생자 수
• 어떤 시간 동안 톨게이트를 통과하는 차량의 수
• 어떤 페이지 하나를 완성하는 데 발생하는 오타의 발생률
• 어떤 특정 량의 방사선을 DNA에 쬐였을 때 발생하는 돌연변이의 수
• 어떤 특정 면적의 다양한 종류의 나무가 섞여 자라는 삼림에서 소나무의 수
• 어떤 특정 진도 이상의 지진이 발생하는 수

푸아송 가정에 어긋나는 사례

• 1분마다 학생회관에 도착할 학생들의 수는 푸아송 분포를 따르지 않을 수도 있다. 왜냐하면, 그 비율이 일정하지 않기 때문이다. (수업 중에는 그 비율이 낮고, 쉬는 시간에는 그 비율이 높을 것이다.) 또, 각 학생들의 도착 사건이 독립적이지 않다. (학생들은 보통 그룹지어서 이동하는 경향이 있다)
• 매년 캘리포니아에서 진도 5의 지진 발생 수는 푸아송 분포를 따르지 않을 것이다. 왜냐하면 한 번의 지진이 그 다음 일어날 지진의 가능성에 영향을 끼치기 때문이다.
• 집중 치료 병동의 환자들 중, 그 병동에서 보낼 날의 수는 푸아송 분포를 따르지 않을 것이다. 왜냐하면, 병동에서 하루도 지내지 않는 경우는 없기 때문이다. 이러한 경우 zero-truncated poisson distribution을 통한 모델링이 가능하다.
• 한 번도 사건이 일어나지 않는 시간 간격의 수가 기본 푸아송 분포를 통해 예측된 것보다 더 많은 경우 (쉽게 생각하면 푸아송 분포에서 계산된 P(k=0)보다 더 높은 P(k=0)을 가지는 경우), zero-inflated 모델을 적용할 수 있다.

다른 분포와의 관계

이항 분포

푸아송 분포는 시행 횟수가 무한히 많아지고, 예상 성공 횟수가 고정되어 있으므로 이항 분포의 한 사례라고 볼 수 있다. 따라서 $n$이 충분히 크고, $p$가 충분히 작으면 이항 분포의 정규 근사로 이끌어 낼 수 있다. 푸아송 분포는 $n$이 100 이상이고, $np$가 10 이하인 경우 좋은 결과값을 얻을 수 있는 근사치라고 판단할 수 있다.

$F_{B}$와 $F_{P}$를 각각 베르누이 분포와 푸아송 분포의 확률 질량 함수라고 하면, 다음과 같은 관계가 나타난다.

$F_{B}(k;n,p)\approx F_{P}(k;\lambda =np)$

이 식을 도출해내는 데에는 확률 생성 함수(probability generating function)를 사용한다. 베르누이 시도에서 한번의 성공의 확률을 $\lambda \leq 1$ 이라고 가정하고 각 간격을 $n$으로 하여 이항 분포로 나타낼 수 있다.

$P_{k}^{(n)}={\binom {n}{k}}\left({\frac {\lambda }{n}}\right)^{k}\left(1-{\frac {\lambda }{n}}\right)^{n-k}$

이 함수의 생성 함수는 다음과 같다.

$P^{(n)}(x)=\sum _{k=0}^{n}p_{k}^{(n)}x^{k}=\sum _{k=0}^{n}{\binom {n}{k}}\left({\frac {\lambda }{n}}\right)^{k}\left(1-{\frac {\lambda }{n}}\right)^{n-k}x^{k}=\sum _{k=0}^{n}{\binom {n}{k}}\left(x{\frac {\lambda }{n}}\right)^{k}\left(1-{\frac {\lambda }{n}}\right)^{n-k}=(1-{\frac {\lambda }{n}}+{\frac {\lambda }{n}}x)^{n}$

여기에서 $n$을 $\infty$로 보내고 곱셈의 극한 정의를 지수 함수로 바꾸면 푸아송 분포의 생성함수로 바뀌게 된다.

$\lim _{n\to \infty }P^{(n)}(x)=\lim _{n\to \infty }\left(1+{\frac {\lambda (x-1)}{n}}\right)^{n}=e^{\lambda (x-1)}=\sum _{k=0}^{\infty }{\frac {e^{-\lambda }\lambda ^{k}}{k!}}x^{k}$

일반적 사항

• 푸아송 분포를 따르고 서로 독립인 확률변수 $X_{1},X_{2}$에 대하여, 확률변수 $Y=X_{1}-X_{2}$는 skellam distribution을 따른다.
• 푸아송 분포를 따르고 서로 독립인 확률변수 $X_{1},X_{2}$에 대하여, $X_{1}+X_{2}=k$라는 조건이 주어진다면 $X_{1},X_{2}$는 종속적이게 되고, $X_{1}+X_{2}$의 조건부 분포 $X_{1}$는 이항 분포를 따른다. $X_{1}|X_{1}+X_{2}=k\sim Binomial\left(k,{\frac {\lambda _{1}}{\lambda _{1}+\lambda _{2}}}\right)$ 두 푸아송 분포의 합이 주어졌을 때 각 변수의 확률을 이항 분포로 모델링 할 수 있다는 것이고, 달리 말하면 두 독립적인 푸아송 분포의 조건부 분포는 이항 분포로 나타낼 수 있다. 일반화하여, $X_{1},X_{2},...,X_{n}$이 매개변수 $\lambda _{1},\lambda _{2},...,\lambda _{n}$를 갖는 서로 독립인 푸아송 확률 변수라면 다음과 같이 이항 분포로 나타낼 수 있다. $X_{i}|\sum _{j=i}^{n}X_{j}=k\sim Binom\left(k,{\frac {\lambda _{i}}{\sum _{j=1}^{n}\lambda _{j}}}\right)$ 더하여, 여러 개의 푸아송 분포를 따르는 변수들이 주어지면, 각 푸아송 변수가 특정 비율로 성공할 확률을 다항 분포(Multinomial distribution)로 나타낼 수 있다. 즉, 여러 개의 서로 독립인 푸아송 변수가 있으면, 그 조건부분포는 다항 분포로 표현될 수 있다. $X_{i}\sim Multinom\left(k,{\frac {\lambda _{i}}{\sum _{j=1}^{n}\lambda _{j}}}\right)$
• $X\sim Pois(\lambda )$ 이고, $X=k$ 일 때, $Y$의 조건부 분포가 $Y|(X=k)\sim B(k,p)$이면, $Y$의 분포는 푸아송 분포 $Y\sim Pois(\lambda p)$를 따른다. 또한, $X=k$일때, $Y_{i}$가 다항 분포를 따르면, $\left\{Y_{i}\right\}|(X=k)\sim Multinom(k,p)$이며, 각 $Y_{i}$는 서로 독립적인 푸아송 분포 $Y_{i}\sim Pois(\lambda p_{i})$를 따른다. 이때 상관계수 $\rho (Y_{i},Y_{j})=0$이다. 즉 두 변수는 선형적 상관관계가 없고, 독립적이다.
• 제곱근 변환: $X$~$Pois(\lambda )$ 인 경우

$Y=2{\sqrt {X}}\approx N(2{\sqrt {\lambda }},1)$ 그리고 $Y={\sqrt {X}}\approx N({\sqrt {X}};1/4)$

이 변환을 거친후에는 변환되지 않은 변수보다 정상성에 대한 수렴이 휠씬 빠르다. 다소 복잡하지만 다른 분산 안정화 변환도 사용 가능한데, 그 중 하나가 앤스컴 변환(Anscombe transform)이다.

• t>0인 모든 t에 대해 시간 간격 [0,t] 내의 도착 횟수가 평균 $\lambda t$인 푸아송 분포를 따르면, 도착간 시간 간격의 차례는 평균 $1/\lambda$인 독립적이고 동일한 지수 분포를 따른다.
• 푸아송 분포와 카이제곱 분포의 누적 분포 함수는 다음과 같은 관계식이 나타난다.

$F_{poisson}(k;\lambda )=1-F_{x^{2}}(2\lambda ;2(k+1)){k|k\in N}$

$P(X=k)=F_{x^{2}}(2\lambda ;2(k+1))-F_{x^{2}}(2\lambda ;2k)$

같이 보기

• 이산 확률 분포
• 이항 분포
• 베르누이 분포

외부 링크

• Prokhorov, A.V. (2001). “Poisson distribution”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. ISBN 978-1-55608-010-4. 
• Weisstein, Eric Wolfgang. “Poisson distribution”. 《Wolfram MathWorld》 (영어). Wolfram Research.