인공 신경망
| 기계 학습과 데이터 마이닝 |
|---|
 |
인공신경망(人工神經網, 영어: artificial neural network, ANN)은 기계학습과 인지과학에서 생물학의 신경망(동물의 중추신경계중 특히 뇌)에서 영감을 얻은 알고리즘이다. 인공신경망은 시냅스의 결합으로 네트워크를 형성한 인공 뉴런(노드)이 학습을 통해 시냅스의 결합 세기를 변화시켜, 문제 해결 능력을 가지는 모델 전반을 가리킨다. 좁은 의미에서는 오차역전파법을 이용한 다층 퍼셉트론을 가리키는 경우도 있지만, 이것은 잘못된 용법으로, 인공신경망은 이에 국한되지 않는다.
인공신경망에는 교사 신호(정답)의 입력에 의해서 문제에 최적화되어 가는 지도 학습과 교사 신호를 필요로 하지 않는 비지도 학습으로 나뉘어 있다. 명확한 해답이 있는 경우에는 교사 학습이, 데이터 클러스터링에는 비교사 학습이 이용된다. 인공신경망은 많은 입력들에 의존하면서 일반적으로 베일에 싸인 함수를 추측하고 근사치를 낼 경우 사용한다. 일반적으로 입력으로부터 값을 계산하는 뉴런 시스템의 상호연결로 표현되고 적응성이 있어 패턴인식과 같은 기계학습을 수행할 수 있다.
예를 들면, 필기체 인식을 위한 신경망은 입력 뉴런의 집합으로 정의되며 이들은 입력 이미지의 픽셀에 의해 활성화된다. 함수의 변형과 가중치가(이들은 신경망을 만든 사람이 결정한다.) 적용된 후 해당 뉴런의 활성화는 다른 뉴런으로 전달된다. 이러한 처리는 마지막 출력 뉴런이 활성화될 때까지 반복되며 이것은 어떤 문자를 읽었는 지에 따라 결정된다.
다른 기계학습과 같이-데이터로부터 학습하는- 신경망은 일반적으로 규칙기반 프로그래밍으로 풀기 어려운 컴퓨터 비전 또는 음성 인식과 같은 다양한 범위의 문제를 푸는데 이용된다.
배경 지식[편집]
인간의 중추 신경계에 대한 조사는 신경망 개념에 영감을 주었다. 생물학적 신경망을 흉내내는 네트워크를 형상하기 위해 인공신경망에서 인공 뉴런들은 서로 연결되어있다.
인공신경망이란 무엇인가에 대한 하나의 공식적인 정의는 없다. 그러나 만약 통계학적 모델들의 집합이 다음과 같은 특징들을 가진다면 해당 집합을 신경(neural)이라고 부른다.
- 조정이 가능한 가중치들의 집합 즉, 학습 알고리즘에 의해 조정이 가능한 숫자로 표현된 매개변수로 구성되어있다.
- 입력의 비선형 함수를 유추할 수 있다.
조정가능한 가중치들은 뉴런 사이의 연결 강도를 의미하고 이들은 훈련 또는 예측하는 동안에 작동한다.
다양한 유닛들이 할당된 하위작업 보다 유닛들에 의한 병렬 혹은 집합적으로 함수들을 수행한다는 점에서 신경망은 생물학적 신경망과 닮았다. '신경망'이라는 단어는 보통 통계학, 인지 심리학 그리고 인공지능에서 사용되는 모델들을 가리킨다. 중추 신경을 모방하는 신경망 모델들은 이론 신경과학과 계산 신경과학의 한 부분이다.
인공신경망을 구현한 현대의 소프트웨어에서는 생물학적 접근법은 신호처리와 통계학에 근거한 좀 더 현실적인 접근법들로 인해 주로 사용되지 않는다. 이러한 시스템들 중 몇몇에서는 신경망 또는 신경망의 부분들(인공 신경들)은 큰 시스템을 형성하며 이러한 시스템은 조정이 가능하거나 기능하지 않은 구성 요소들로 결합되어 있다. 이러한 시스템의 일반적인 접근법은 많은 현실 문제 해결에 적합한 반면에 전통적인 인공지능 연결 모델에서는 그렇지 않다. 그러나 이들에게도 공통점이 있는데 그것은 비선형의 원리 분산, 병렬과 지역 처리 그리고 적응이다. 역사적으로 신경 모델들의 이용은 18세기 후반 if-then 규칙으로 표현된 지능을 가진 전문가 시스템을 특징으로 하는 고차원(symbolic) 인공지능에서부터 동적 시스템의 매개변수들을 가진 지능을 특징으로 하는 저차원(sub-symbolic) 기계학습으로 가는 패러다임의 변환이다.
역사[편집]
워런 맥컬록(Warren McCulloch)와 월터 피츠(Walter Pitts)는[1] (1943) 수학과 임계 논리(threshold logic)라 불리는 알고리즘을 바탕으로 신경망을 위한 계산학 모델을 만들었다. 이 모델은 신경망 연구의 두 가지 다른 접근법에 대한 초석을 닦았다. 하나의 접근법은 뇌의 신경학적 처리에 집중하는 것이고 다른 하나는 인공 신경망의 활용에 집중하는 것이다.
1940년 후반에 심리학자 도널드 헤비안(Donald Hebb)는[2] 헤비안 학습(Hebbian learning)이라 불리는 신경가소성의 원리에 근거한 학습의 기본 가정을 만들었다. 헤비안 학습은 전형적인 자율학습으로 이것의 변형들은 장기강화(long term potentiation)의 초기 모델이 된다. 이러한 아이디어는 1948년 튜링의 B-type 기계에 계산학 모델을 적용하는데서 출발하였다.
팔리(Farley)와 웨슬리 클라크(Wesley A. Clark)는[3](1954) MIT에서 헤비안 네트워크를 모의 실험하기 위해 처음으로 계산학 모델(후에 계산기라 불리는)을 사용하였다. 다른 신경망 계산학 기계들은 로체스터(Rochester), 홀랜드(Holland), 하빗(Habit), 두다(Duda)에 의해 만들어졌다.[4] (1956)
프랑크 로젠블랫(Frank Rosenblatt)는[5] (1958) 퍼셉트론 즉, 간단한 덧셈과 뺄셈을 하는 이층구조의 학습 컴퓨터 망에 근거한 패턴 인식을 위한 알고리즘을 만들었다. 계산학 표기법과 함께 로벤블라트는 또한 기본적인 퍼셉트론에 대한 회로가 아닌예를 들면 배타적 논리합 회로(exclusive-or circuit)와 같은 회로를 표기하였다. 해당 회로의 수학 계산은 폴 웨어보스(Paul Werbos)에 의해 오차역전파법이 만들어진 후에 가능하였다.[6] (1975)
마빈 민스키(Marvin Minsky)와 시모어 페퍼트(Seymour Papert)에 의해 기계학습 논문이 발표된 후에[7] (1969) 신경망 연구는 침체되었다. 그들은 인공신경망에서 두 가지 문제점을 찾아내었다. 첫 번째로는 단층 신경망은 배타적 논리합 회로를 처리하지 못한다는 것이다. 두 번째 중요한 문제는 거대한 신경망에 의해 처리되는 긴 시간을 컴퓨터가 충분히 효과적으로 처리할 만큼 정교하지 않다는 것이다. 신경망 연구는 컴퓨터가 충분히 빨라지고, 배타적 논리합 문제를 효율적으로 처리하는 오차역전파법이 만들어지기까지 더디게 진행되었다.
1980년대 중반 병렬 분산 처리는 연결주의(connectionism)라는 이름으로 각광을 받았다. 데이비드 럼멜하트(David E. Rumelhart)와 제임스 맥클레랜드(James McClelland)가 쓴 교과서는[8] (1986) 연결주의를 이용해 신경 처리를 컴퓨터에서 모의 실험하기 위한 모든 것을 설명하였다.
인공신경망이 어느정도 뇌의 기능을 반영하는지 불분명하기 때문에 뇌 신경 처리의 간단한 모델과 뇌 생물학적 구조간의 상관관계에 대해 논란 중에 있으나 인공지능에서 사용되는 신경망은 전통적으로 뇌 신경 처리의 간단한 모델로 간주된다.[9]
인공신경망은 SVM과 같은 다른 기계학습 방법들의 인기를 점차적으로 추월하고 있다. 2000년대 이후 딥 러닝의 출현이후 신경 집합의 새로운 관심은 다시 조명받고 있다.
2006년 이후 발전 동향[편집]
생물물리학 모의실험 그리고 뇌신경학 컴퓨팅을 위한 계산학 디바이스들은 CMOS를 통해 만들어졌다. 최근에는 큰 범위의 기본 요소들의 분석과 합성을 위한 나노 디바이스 제작과 같은 노력들이 있다.[10] 만약 성공한다면 이러한 노력은 디지털 컴퓨팅을 뛰어넘는 신경 컴퓨팅의 새로운 시대를 도래하게 할 것이다.[11] 왜냐하면 이것은 프로그래밍 보다는 학습에 기반하며 비록 첫 예시가 CMOS 디지털 디바이스와의 합작일지라도 이것은 기본적으로 디지털보다 아날로그이기 때문이다.
2009년부터 2012년동안 스위스 AI 연구실 IDSIA에서 위르겐 슈밋흠바(Jürgen Schmidhuber)의 연구 그룹이 개발한 재귀 신경망과 심화 피드포워드 신경망은 여덞 번의 패턴 인식과 기계학습 국제 대회에서 우승하였다.[12][13] 예를 들면, 알렉스 그레이브스(Alex Graves et al)의 쌍방향 그리고 다중 차원의 장단기 기억(LSTM)은[14][15][16][17] 2009년의 국제문서 분석 및 인식 컨퍼런스(ICDAR)의 필기 인식 부분에서 학습하게 될 세 가지 언어에 대한 아무런 사전 정보가 주어지지 않았음에도 불구하고 세 번이나 우승하였다.
IDSIA의 댄 크리슨(Dan Ciresan)과 그 동료들에 의한 빠른 GPU 기반 실행 접근 방법은 IJCNN 2011 교통 표지판 인식 대회,[18][18] ISBI 2012 신경 구조의 분할의 전자 현미경 대회를 비롯하여 여러 패턴 인식 경연에서 여러 번 우승하였다.[19] 그들의 신경망은 또한 처음으로 교통 표지판(IJCNN 2012) 또는 MINIST 필기 인식 분야에서 인간과 견줄만한 또는 인간을 넘어서는 인공 패턴 인식이다.[20]
심화 비선형 신경 아키텍처는 1980년 후쿠시마 구니히코(Kunihiko Fukushima)의 신인식기(neocognitron)와 비슷하다.[21] 그리고 일차 시각 피질에서 데이비드 허블(David H. Hubel)과 토르스텐 비셀(Torsten Wissel)에 의해 밝혀진 간단하고 복잡한 세포들에 영감을 받은 표준 비전 아키텍처는[22] 토론토대학의 조프 힌턴(Geoff Hinton) 연구실의 자율학습 방법에 의해 미리 훈련된다.[23][24] 해당 연구실의 팀은 2012년 베르크(Berck)의 후원을 받는 신약 개발에 필요한 분자들을 찾는데 도움을 주는 소프트웨어 제작 대회에서 우승하였다.[25]
모델[편집]
인공지능 분야에서 신경망은 보통 인공신경망을 지칭한다. 인공신경망은 본질적으로 함수 , 에 대한 분포, 또는 와 에 대한 분포를 정의하는 간단한 수학적 모델이고, 가끔씩 특정한 학습 알고리즘이나 학습 규칙과 긴밀하게 연계되어 있기도 한다. 인공신경망이라는 단어는 보통 이러한 함수들의 모임에 대한 정의를 뜻하고, 이 모임의 구성원들은 식의 인자를 바꾸거나, 연결 가중치를 바꾸거나, 뉴런의 수나 연결 정도와 같은 구조에 대한 상세적인 것을 바꿈으로써 얻어진다.
망 함수[편집]
단어 '인공신경망'에서 망은 각 시스템에 있는 여러 층의 뉴런 간의 연결을 의미한다. 예를 들어 세 층이 있는 시스템이 있다면, 첫 번째 층은 시냅스를 통해 두 번째 층의 뉴런들로 데이터를 보내는 입력 뉴런들이 있고, 더 많은 시냅스를 통해 세 번째 층의 출력 뉴런으로 신호를 보내는 식이다. 시스템이 더 복잡해질수록 뉴런 층의 수도 더 많아지고, 그 층 안에 있는 입력 뉴런과 출력 뉴런들의 수도 많아질 것이다. 이 시냅스들은 계산 과정에서 데이터 값을 조절하는 가중치 값을 저장한다.
인공신경망은 보통 세 가지의 인자를 이용해 정의된다.
- 다른 층의 뉴런들 사이의 연결 패턴
- 연결의 가중치를 갱신하는 학습 과정
- 뉴런의 가중 입력을 활성화도 출력으로 바꿔주는 활성화 함수
수학적으로, 뉴런의 망 함수 는 다른 함수 들의 합성으로 정의되고, 이 함수들 또한 다른 함수들의 합성으로 정의될 수 있다. 이 함수는 화살표가 변수들 사이의 의존 관계를 나타내는 망 구조로써 편리하게 나타낼 수 있다. 자주 쓰이는 종류의 합성으로는 비선형 가중 합이 있는데, 쌍곡선함수와 같은 미리 정의된 함수 (주로 활성화 함수라 불림[26])가 있을 때 로 나타내어지는 함수를 뜻한다. 이하 설명의 편리함을 의해 함수 들의 모임을 간단히 벡터 로 취급하자.

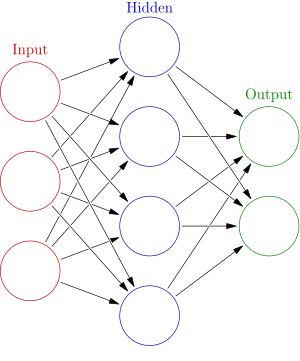
이 그림은 변수들 사이의 의존 관계를 화살표로 나타내는 망 구조로 를 분해해 나타낸 것이다. 이 그림은 두 가지 관점으로 해석할 수 있다.
첫 번째 관점은 함수로써 바라보는 것이다. 입력값 가 3차원 벡터 로 변환 된 다음, 2차원 벡터 로 변환되고 최종적으로 출력값 으로 변환된다. 이 관점은 최적화에 대해 이야기할 때 제일 흔하게 접할 수 있다.
두 번째 관점은 확률론적으로 바라보는 것이다. 확률변수 는 확률변수 에 의존하고, 이것은 에 의존하고, 또 이것은 확률변수 에 의존한다. 이 관점은 그래프 모형에 대해 이야기할 때 제일 흔하게 접할 수 있다.
이 두 관점은 대체로 같다고 볼 수 있다. 두 경우 모두 이 망 구조에 대해 각각의 층의 구성 요소는 서로 독립적이다 (의 요소들은 로부터의 입력이 주어졌을 때 서로 독립이다). 이것은 구현할 때 어느 정도의 병렬화를 가능하게 해 준다.

앞의 예와 같은 신경망은 의존 관계를 나타내는 화살표가 한 방향으로만 나아가는 유향 비순환 그래프이기 때문에 전향 신경망이라고 불린다. 순환이 있는 망은 재귀 신경망이라고 불린다. 재귀 신경망은 그림 위쪽과 같이 가 자기 자신에 의존적인 것으로 나타내어지지만, 시간적 의존 관계는 보이지 않는다.
학습[편집]
신경망이 관심을 받는 제일 큰 요소는 바로 학습이 가능하다는 것이다. 해결해야 되는 주어진 과제와 함수 들의 모임이 주어졌을 때, 학습을 한다는 것은 과제를 어떤 최적화된 방법으로 푸는 를 관측값들을 이용해 푼다는 것이다.
학습을 한다는 것은 최적해 에 대해 인 비용 함수 를 정의하는 것을 수반한다. 다시 말해, 정의된 함수 에 대해, 최적해의 비용보다 더 적은 비용을 필요로 하는 해답은 존재하지 않는다는 것이다. (수학적 최적화 참고.)
비용 함수 는 특정한 해답이 해결할 문제의 최적해에 대해 얼마나 떨어져 있는지에 대한 측도이기 때문에 학습에 있어 중요한 개념이다. 학습 알고리즘은 해답들의 모임 에서 최소 비용을 필요로 하는 함수를 찾아나가는 식으로 작동한다.
해답이 어떤 데이터에 의존적인 경우, 비용은 관측값에 대한 함수가 되어야 하며, 그렇지 않을 경우에는 데이터와 관련된 어떤 것도 모델링할 수 없게 된다. 많은 경우 비용은 근사될수만 있는 통계로 주어진다. 간단한 예로, 어떤 분포 에서 뽑아낸 데이터 쌍 에 대해 비용 을 최소화하는 모델 을 찾는 문제를 생각해 보자. 실용적으로는 분포 에서 유한한 개의 샘플만을 뽑아낼 수 있으므로, 이 예의 경우 , 즉 전체 데이터 집합이 아니라 데이터의 샘플에 대한 비용만 최소화될 수 있을 것이다.
이 매우 크거나 무한하다면, 새 예제가 주어질 때마다 비용이 부분적으로 최소화되는 온라인 알고리즘을 사용해야 한다. 가 고정되어 있을 때 직결 기계 학습을 종종 사용하기는 하지만, 분포가 시간에 따라 서서히 변할 때 사용하는 것이 더 유용하다. 신경망을 사용할 때에는, 직결 기계 학습을 유한한 자료 집합에 대해 자주 사용하기도 한다.
비용 함수 고르기[편집]
임의의 비용 함수를 그때그때 정의할 수도 있지만, 일반적인 경우 (볼록성과 같은) 원하는 성질을 가지거나 (확률론적 공식화에서 모델의 사후 확률을 비용의 역으로 생각하는 것과 같이) 문제의 특정한 공식화에서 자연스레 나타난다던지 하는 이유로 특정한 비용 함수를 사용한다. 결과적으로 비용 함수는 원하는 과제에 따라 달라진다. 학습 과제는 학습 패러다임에 따라 아래와 같이 세 분류로 묶을 수 있다.
학습 패러다임[편집]
학습 패러다임에는 크게 지도 학습, 자율 학습, 준 지도 학습이 있으며, 각각이 특정한 추상적인 학습 과제에 대응된다.
지도 학습[편집]
지도 학습에서는 예제 들의 집합이 주어졌을 때, 가능한 함수 들의 목록 중 예제에 제일 적합한 함수를 고르는 것을 목표로 한다. 즉, 주어진 데이터로부터 함수를 추론하는 것이다. 이 때 비용 함수는 주어진 데이터가 추론한 함수와 얼마나 어긋나느냐에 따라 달려 있고, 문제에 대한 사전 지식을 암시적으로 포함하고 있다.
흔히 모든 예제쌍에 대한 망의 출력 과 목표값 의 평균 제곱 오차를 최소화하는 평균 제곱 오차를 비용 함수로 사용한다. 이 비용을 최소화하기 위해 다층 퍼셉트론이라 불리는 신경망의 한 분류에 경사 하강법을 이용한다면, 이것은 신경망을 학습하기 위해 널리 쓰이는 오차역전파법이 된다.
지도 학습 패러다임에 해당하는 과제에는 패턴 인식 (또는 분류)와 회귀분석 (또는 함수 근사)가 있다. 지도 학습은 음성인식이나 모션 인식 분야에 나타나는 순차적 데이터에도 적용시킬 수 있다. 이것은 현재까지 얻어진 답의 품질에 대해 계속해서 피드백을 주는 함수의 형태로서의 "선생님"과 같이 배우는 것으로 생각할 수 있다.
자율 학습[편집]
자율 학습에서는 데이터 가 주어졌을 때 데이터 와 망의 출력 에 대한 임의의 비용 함수를 최소화한다.
비용 함수는 할 과제(모델링할 것)와 선험적 가정(모델, 모델의 변수와 관측된 변수에 대한 암시적인 성질)에 따라 결정된다.
간단한 예로, 비용함수 가 주어져 있고 가 상수일 때 모델 에 대해 생각 해 보자. 비용을 최소화하면 데이터의 평균인 값이 나올 것이다. 비용 함수는 이것보다 훨씬 더 복잡해질 수 있고, 그 꼴은 어디에 사용되느냐에 따라 달려 있다. 예를 들어, 압축과 관련된 과제에서는 와 사이의 상호 정보량과 관련이 있는 비용 함수를 사용할 수 있고, 통계 모델링에서는 데이터가 주어졌을 때 모델의 사후 확률과 관련지을 수 있을 것이다. (참고로 두 경우 모두 이 값을 최소화하는 게 아니라 최대화해야 된다. 이론적으로는 이 값의 역수를 비용 함수로 사용하면 될 것이다.)
자율 학습 패러다임에 속하는 과제는 일반적으로 근사와 관련된 문제들이다. 클러스터링, 확률 분포의 예측, 데이터 압축, 베이지언 스팸 필터링 등에 이것을 응용할 수 있다.
준 지도 학습[편집]
준 지도 학습에서 데이터 는 주어지지 않고, 대신 행위자가 환경과 상호 작용을 함으로써 생성된다. 시간의 매 순간 마다, 행위자는 행동 를 취하고 환경에서 와 순간적인 비용 가 알려지지 않은 특정한 법칙에 따라 생성되어 관측된다. 이 때 목표는 예상되는 장기적 (누적) 비용을 최소화하는 특정한 행동을 고르는 정책을 찾는 것이다. 환경의 법칙과 각각의 정책에 따른 장기적 비용은 보통 모르지만, 예측할 수는 있다.
형식적으로 말해 환경은 상태 와 행동 이 순간적인 비용의 분포 , 관측 분포 , 상태 천이 분포 와 함께 주어진 마르코프 결정 프로세스로 모델링되며, 정책은 관측값들이 주어졌을 때 행동에 대한 조건부 분포로 정의된다. 이 두가지는 함께 마르코프 연쇄를 이룬다. 목표는 비용을 최소화하는 정책, 즉, 비용이 최소인 마르코프 연쇄를 찾는 것이다.
인공신경망은 전체적인 알고리즘의 일부로서 준 지도 학습에 자주 이용된다.[27][28] 동적 계획법은 베르트세카스(Bertsekas)와 치치클리스(Tsitsiklis)[29]에 의해 인공신경망과 결부되었으며, 차량 경로 설정 문제,[30] 천연 자원 관리[31][32], 의학[33] 등에 관련된 다차원 비선형적 문제에 적용되었는데, 원래 제어 문제의 해답을 수치적으로 근사하기 위한 이산화 격자의 간격을 넓혀서 생기는 정확도 감소 문제를 인공신경망이 완화시킬수 있기 때문이다.
준 지도 학습 패러다임에 속하는 과제에는 제어 문제, 게임, 순차적 결정 문제 등이 있다.
학습 알고리즘[편집]
실질적으로 인공신경망을 학습시키는 것은 비용을 최소화하는 모델을 허용된 모델의 집합에서 고르는 것이다. (베이즈 확률론에서는 허용된 모델의 집합 상에서 모델의 분포를 결정짓는 것이다.) 인공신경망을 학습시키는 데에는 많은 알고리즘이 존재하고, 그 중 대부분은 최적화 이론과 추정 이론을 접목해 응용한 것으로 볼 수 있다.
인공신경망을 학습할 때 사용하는 대부분의 알고리즘은 역전파 기법을 이용해 실제 기울기를 계산하는 경사 하강법을 사용한다. 이는 간단하게 비용 함수를 망의 인자에 대해 미분한 다음 인자를 기울기 방향으로 조금씩 바꾸는 식으로 할 수 있다.
유전 알고리즘,[34] 유전자 수식 프로그래밍,[35] 담금질 기법,[36] 기댓값 최대화 알고리즘, 비모수 통계, 군집 최적화[37]와 같은 방법들이 신경망을 학습시키는데 주로 이용된다.
인공신경망의 사용 방법[편집]
인공신경망의 가장 큰 장점은 관찰된 데이터로부터 학습하여 원하는 근사 함수를 만들 수 있다는 것이다. 그러나 사용하려는 신경망의 기본 이론과 예측하려는 데이터의 근본적인 이해가 매우 중요하다. 인공신경망의 사용함에 있어서 세가지 큰 부분으로 나눌 수 있다.
- 모델의 선택: 예측 하려는 데이터를 어떤방법으로 표현 하는지에 대한 선택이다. 지나치게 복잡한 모델은 학습 과정에서 Overfitting 문제가 발생 할 수 있다.
- 학습 알고리즘: 학습 알고리즘 사이에 많은 장단점이 있다. 대부분의 알고리즘은 hyperparameters와 함께 고정된 데이터 집단에서 잘 동작한다. 하지만 알려지지 않은 데이터의 예측의 경우 대부분 많은 시간과 연구가 필요하다.
- 견고함: 모델과 알고리즘이 적절하게 선택되었다면 인공신경망의 결과는 매우 높은 예측 값을 가진 것이다.
인공신경망의경우 자연스럽게 많은 데이터를 가지고 online learning 방식을 사용한다. 이 방식은 병렬화가 쉽게 가능하도록 주로 지역적 의존성만 가지고 있다.
적용[편집]
인공신경망의 활용은 데이터 관찰로부터 원하는 함수를 추론 하는데 사용할 수 있다. 이것은 매우 복잡한 데이터를 사용하거나 사람의 주관적인 판단이 필요한 부분에 매우 유용하게 사용될 수 있다.
실생활에서 적용[편집]
인공 신경망은 다음과 같은 몇가지 종류로 사용될 수 있다.
- 함수 추론, 회귀 분석, 시계열 예측, 근사 모델링
- 패턴 인식 및 순서 인식 그리고 순차 결정 같은 분류 알고리즘
- 필터링, 클러스터링, 압축 등의 데이터 처리
- 인공 기관의 움직임 조정 같은 로봇 제어
- 컴퓨터 수치 제어
또한 인공신경망은 여러 가지 암 진단에도 사용되었다. HLDN이라는 인공 신경망 기반 폐암 검출 시스템은 암 진단의 정확성과 속도 향상을 이루었고 전립선 암에도 사용되었다.[38] 이 시스템은 많은 환자의 데이터로부터 특정한 모델을 만들어서 모델과 환자 한명과 비교를 통해서 진단한다.모델은 다른 변수의 상관관계나 가정에 의존하지 않는다. 인공 신경망 모델은 임상 실험 방법보다 더 정확하게 동작하였고 한 기관에서 훈련된 모델이 다른 기관에서도 결과를 예측 할 수 있었다.
신경 네트워크와 신경 과학[편집]
이론 및 계산 신경과학은 이론적 분석과 생물학적 신경 시스템의 컴퓨터 모델링과 관련된 분야이다. 인공 신경망이 인식 과정이나 행동에 상당히 관련이 되어있는 것과 같이 신경 과학 분야도 밀접하다. 이 분야의 목적은 생물학적 신경 시스템 모델을 사용해서 생물학적 시스템이 어떻게 동작하는지 이해 하는 것이다. 이 분야를 이해하기 위해서 신경과학자들은 관측된 생물학적 프로세스와 생물학적 메카니즘 사이의 링크를 만들기 위해서 신경 학습과 이론을 적용하고 있다.
다양한 모델의 종류[편집]
다양한 모델이 추상화 단계에서 시스템의 특성에 따라 다르게 적용이 된다. 다양한 모델들 각각 신경 세포와 신경 회로의 관계가 최종 시스템이 추상적 신경 모델에서 발생 할 수 있는 상호작용과 단기 행동 모델까지 다양한 모델들이 있다. 이러한 신경 시스템모델들은 각각 신경 세포와 시스템 간의 상호 관계에 따라 달라진다.
경영학에서의 인공신경망[편집]
인공신경망을 경영학에 응용하고자 하는 연구는 재무, 회계, 마케팅, 생산 등의 분야에서 다양하게 진행되어 왔다. 특히, 재무분야에 대한 응용연구는 매우 활발하게 진행되고 있는데 주가지수예측, 기업신용평가, 환율예측 등의 연구가 진행되고 있다.
인공 신경망 소프트웨어[편집]
인공 신경망 소프트웨어는 시뮬레이션, 연구, 개발 분야에 많이 사용된다. 인공 신경망 소프트웨어는 생물학적 신경망 개념을 가져와서 여러 가지 시스템에 적용되고 있다.
시뮬레이션[편집]
인공 신경망 시뮬레이터는 대부분 생물학적 신경망이나 인공 신경망을 구현하는 프로그램으로 사용된다. 보통 한가지 이상의 신경망 종류를 제공 한다. 대부분 시뮬레이터들은 학습 방법을 데이터 시각화 하는 기능을 제공한다.
- 연구 시뮬레이터: 전통적으로 가장 많이 사용되는 인공 신경망 시뮬레이터이다. 가장 중요한 목적은 신경망의 정확한 행동이나 특징을 시각화나 데이터로 이해하기 편하게 한다.
- 데이터 분석 시뮬레이터: 실용적인 프로그램에 많이 사용된다. 데이터 마이닝이나 예측에 사용되고 항상 많은 전처리 과정을 거치게 된다.
- 인공 신경망 교육 시뮬레이터: 기본적인 프로그래밍 지식 없이 인공 신경망을 사용 해볼 수 있는 프로그램이다. 작고 사용하기 쉬운 시뮬레이터는 간단한 전방 전달(feed forward)과 오차역전파법(back propagation) 알고리즘을 제공한다.
개발 환경[편집]
인공 신경망 개발 환경은 대부분 강력한 기능을 제공한다. 알고리즘 수정이 쉽고 다른 프로그램과 같이 사용하기 편하다. 어떤 프로그램은 좋은 전처리 알고리즘과 시각화 알고리즘도 제공한다.
- 구성 요소 기본 개발: 최근 개발 환경은 구성 요소 기본 개발 환경을 선호한다. 어댑터나 파이프를 사용해서 구성 요소와 연결하여 결과를 처리하는데 매우 높은 유연성을 가지고 있고 어느 프로그램 환경에서나 동작 할 수 있다. 단점으로는 컴포넌트 동작을 위해서 많은 지식이 요구가 된다.
사용자 개발 인공 신경망[편집]
인공 신경망의 가장 많은 형태는 사용자가 직접 다양한 환경에서 구현한 경우이다. 높은 유연성을 가지고 있지만 개발하기 힘들다는 단점이 있다. 연구분야 뿐만 아니라 실제 서비스등 많은 분야에서 사용된다.
신경망 알고리즘 종류[편집]
인공 신경망 유형은 복잡한 다중 입력과 방향성 피드백 루프와 단방향 또는 양방향 그리고 다양한 계층등 여러 가지 종류가 있다. 전반적으로 이들 시스템의 알고리즘은 각각 함수의 제어와 연결을 결정하게 된다. 대부분의 시스템은 "가중치"와 다양한 신경들의 연결을 시스템의 매개 변수를 수정하는데 사용된다. 인공 신경망은 자동적으로 외부의 훈련으로부터 자동적으로 학습을 하거나 스스로 데이터를 사용해서 발전 될 수 있다.
- 전방 전달 신경망(Feedforward neural network): 가장 간단한 방법의 인공신경망 방법이다. 신경망 정보가 입력 노드에서 은닉노드를 거쳐 출력 노드까지 전달 되며 순환 경로가 존재하지 않는 그래프를 형성한다. 다양한 방법의 구조가 존재하는데 이진 구조, 퍼셉트론, 시그모이드 등등 여러 가지 방법으로 구성 할 수 있다.
- 방사 신경망(Radial basis function network): 방사상 인공 신경망은 다차원의 공간의 보간법에 매우 강력한 능력을 가지고 있다. 방사 함수는 다 계층의 시그모이드 함수를 은닉 노드에서 사용하는 형태를 대체할 수 있다.
- 코헨 자기조직 신경망(kohonen self-organizing network): 자기조직 신경망 알고리즘은 대표적인 신경망 알고리즘중 하나로 대부분의 신경망 알고리즘이 지도(supervised) 학습방법을 사용하는 것과는 대조적으로 자율(unsupervised) 학습방법과 경쟁(competitive) 학습방법을 사용한다. 신경망은 입력층과 경쟁층으로 나뉘고, 경쟁층의 각 뉴런은 연결강도 백터와 입력백터가 얼마나 가까운가를 계산한다. 그리고 각 뉴런들은 학습할 수 있는 특권을 부여 받으려고 서로 경쟁하는데 거리가 가장 가까운 뉴런이 승리하게 된다. 이 승자 뉴런이 출력신호를 보낼 수 있는 유일한 뉴런이다. 또한 이 뉴런과 이와 인접한 이웃 뉴런들만이 제시된 입력 백터에 대하여 학습이 허용된다.
- 순환 인공 신경망(Recurrent neural network): 순환 인공 신경망은 전방 신경망과 정 반대의 동작을 한다. 노드들 간의 양방향 데이터 이동이하며 데이터는 선형적으로 전달이 된다. 데이터가 후방 노드에서 전방노드로 전달하여 연산이 수행될 수 도 있다.
이론적 특성[편집]
계산 능력[편집]
다층 퍼셉트론(MLP)은 보편 근사 정리로 증명된 일반적인 함수 근사자이다. 하지만, 이 증명은 인공신경망에 필요한 신경의 수나 가중치의 설정에 직접적으로 관여하지 않는다.
하바 세이겔만(Hava Siegelmann)과 에드워도 다니엘 손택(Eduardo D. Sontag)의 연구 [39]는 유한개의 수로 이루어진 신경들과 일반 선형 연결을 사용한 어떤 합리적인 가중치의 값(정확한 실수 값의 가중치가 아니라)을 가진 어떤 반복되는 구조는 일반적인 튜링 기계와 동일하게 완벽한 성능(full power of a Universal Turing Machine)을 가진다는 것을 증명했다. 게다가, 비합리적인 값의 가중치 설정은 기계로 하여금 튜링 기계이상의 성능(super-Turing power)을 발휘하게 한다는 것도 이미 증명되었다[40].
수용력(Capacity)[편집]
인공신경망 모델은 수용력이라고 불리는 특성을 가지고 있으며, 그것은 신경망에서 주어진 함수 모델의 능력에 상당히 연관된다. 또한 신경망에 저장될 수 있는 어떤 정보의 총량과 정보 개념의 복잡도와 크게 연관된다.
근사(Convergence)[편집]
인공신경망을 계산할 때는 항상 근사에 대한 몇가지 문제에 직면하게 된다. 첫번째로, 국지적 최솟값이 존재할 수 있다는 것이다. 이것은 신경망의 비용(Cost)함수와 모델에 좌우된다. 두번째로, 알려진 최적화 방법은 국지적 최솟값과 멀리 떨어져 있을 때 적당한 근사를 보장하지 않을 수 있다는 점이다. 세번째로, 상당히 큰 양의 데이터나 변수들에 대해서 일부 이미 알려진 알고리즘들은 비현실적일 수 있다. 일반적으로, 근사에 대한 이론적 보장은 실생활 데이터의 적용에서는 신뢰할 만 하지 않을 수 있다고 알려져 있다.
일반화와 통계[편집]
실제 적용에서의 목표는 신경망에 학습 되지 않은 숨겨진 예시에 대해서도 정확한 추측을 가능하게 되는 것이지만, 이를 위한 과도한 트레이닝은 문제를 일으킬 수 있다. 즉, 필요한 자유 매개변수에 대해 네트워크의 용량이 이를 엄청나게 초과했을 때에는 시스템에 복잡한 문제가 발생될 수 있다. 이러한 문제를 피하기 위한 두가지 해결책이 제시되었다.
첫 번째는 교차타당화(cross-validation)와 비슷한 방법으로, 현재 신경망이 과도한 트레이닝이 되었는지 지속적으로 확인하고 에러를 최소화하며, 신경망 학습을 최적화 하기 위해 특수한 매개변수(Hyperparameters)를 선택하는 방법이다. 두번째 제시된 방법은 정칙화(Regularization)이다. 이 개념은 확률적(베이지안) 프레임워크에서 자연적으로 드러난다. 즉, 정칙화는 쉬운 신경망 모델들 중에서 더 큰 우선순위를 가지는 확률을 선택함으로써 수행될 수 있다. 하지만 통계적 학습이론에서도, 궁극적인 목표는 경험에 의한 위험성(Empirical risk)과, 구조적 위험성(Structural risk)의 두가지 값을 최소화하는 것이다. 이것들은 훈련집합 자체의 오류 및 과도한 훈련 및 학습으로 인해 숨겨졌던 자료에 대한 예고되는 오류와 크게 상관있는 것으로 알려져 있다.
평균제곱오차 비용함수를 사용하는 교사 학습된 신경망은 학습된 모델의 신뢰도를 결정하기 위해 이미 알려진 여러 가지 통계 방법을 사용할 수 있다. 예를 들어, 검증집합의 평균제곱오차는 분산을 측정할 때 사용될 수 있다. 또한 이 값이 정규분포를 따른다고 가정하면, 네트워크의 출력 값의 신뢰 구간을 계산하는데 사용될 수 있다. 출력 확률 분포는 동일하게 유지하고 네트워크가 수정되지 않기 때문에 이렇게 만든 신뢰도 분석은 통계적으로 유효하다. 범주 대상 변수를 위한 신경망 (또는 컴포넌트 기반 뉴럴 네트워크에서 softmax 성분)의 출력층에 softmax 활성화 함수, 즉 로지스틱 방정식의 일반화를 할당하여, 출력은 사후 확률로 해석 될 수 있다. 이것은 분류할 때 확실한 측정값을 주기 때문에 이에 매우 유용하다.
softmax 활성화 함수는 일반적으로 아래와 같이 나타내어진다.
인공신경망의 시뮬레이션을 할때, Softmax 함수는 신경망 마지막층의 분류계산을 하기 위해 구현된다. 일반적인 로그-손실(log loss) 또는 교차-엔트로피(Cross-entropy) 방식으로 학습된 신경망에서는, 다항 로지스틱 회귀분석(multinomial logistic regression)의 비선형 도함수(Derivative)를 가질 수 있다.
함수 지도 벡터와 특수 인덱스 i를 실수 값으로 보면, 도함수(Derivative) 식은 아래와 같이 인덱스를 고려해야 한다.
여기서, 크로네커 델타는 단순화를 위해 사용된다.(이것은 함수 그 자체로 표현되는 시그모이드 함수의 도함수(Derivative)와 비교될 수있다.)
인공신경망에 대한 논란[편집]
학습 문제[편집]
인공신경망 중에서도 로보틱스 분야는 많은 비평가들에게 비판을 받는다. 왜냐하면 실제 상황에 정확히 부합하는 작동을 학습하기 위해 수많은 경우에 대한 엄청난 다양성을 가진 자료의 수집을 필요로 하기 때문이다. 하지만 이것은 그리 놀랄 일이 아니다. 어떠한 학습 기계(Learning machine)라도 여러 가지 새로운 케이스에 정확히 동작하는 근본적인 구조를 잡기위해 수 많은 훈련 예시들을 필요로 하기 때문이다. 딘 포말리우(Dean Pomerleau)의 최근 논문 “자동 로봇 운전을 위한 인공신경망의 지식기반 학습 방법”에서는 여러 가지 종류의 길을 갈 수 있는 로봇 자동차를 훈련하기 위해 인공신경망이 사용된다. 그의 연구의 대부분은 하나의 학습 경험으로부터 여러개의 학습 시나리오를 추정하는 것과 과거 학습의 다양성을 유지하여 시스템이 과도하게 학습하는 것을 막는 것, 이 두가지에 기울여져 있다.(예를 들어, 이 연구에서는 과거에 학습된 우회전을 잊지 않고, 비슷한 상황에서 언제나 우회전을 하게 학습하는 것을 막게 할 수 있다.) 실제 상황의 넓고 다양한 반응에 대해서 어떤 것을 훈련하고 선택할 것인지와 같은 문제는 인공신경망에서는 상당히 일반적이다.
미국인 과학 칼럼니스트 알렉산더 듀드니(A. K. Dewdney)는 1997년 쓴 글에서, "비록 신경망이 매우 적은 장난감과 같은 문제를 풀지라도, 그 계산 능력은 일반적인 문제 해결 기법들을 가뿐히 뛰어넘을 정도의 수준을 가질 수 있다." 라고 적었다.
하드웨어 문제[편집]
크고 효과적인 인공신경망 소프트웨어를 구현하기 위해서는 상당한 프로세싱 기법과 저장 자원이 필요하다. 우리의 뇌는 신경 그래프를 통한 신경전달 프로세싱 임무에 최적화된 하드웨어를 가지고 있다. 우리가 가장 간단하게 시뮬레이션 할 수 있는 폰 노이만 기술 조차도 신경망 디자이너로 하여금 뇌와 같은 신경 그래프를 구축하기 위해 수백, 수천만 개의 데이터베이스 행을 채우도록 하고 있다. 이는 엄청난 양의 컴퓨터 메모리와 하드디스크 공간을 소비하게 한다. 게다가, 신경망 시스템의 디자이너는 이런 엄청난 신경 연결과 뉴런들을 통해 뇌와 같은 신호 전달을 시뮬레이션 할 수 있어야 한다. 이것은 일반적인 CPU의 처리능력과 시간으로는 불가능한 양일 정도이다. 하지만, 신경망은 가끔 효과적인 프로그램을 만들어 낼 수 있게 해주고 비용적 측면에서도 효율적이고 고려할만한 정도의 효과를 내 줄 때가 있다. 게다가 컴퓨터의 계산능력은 무어의 법칙에 따라 지속적으로 크게 증가하고 있으며, 이는 새로운 임무를 효과적으로 달성하는데 기여하고 있다. 또한 신경모방 공학에서는 처음부터 신경망을 구현하기 위해 설계된 회로(비 폰 - 노이만 칩)를 구성하여, 직접적으로 하드웨어적 어려움을 해결하기 위해 노력하고 있다.
실제 반례에 대한 비판[편집]
알렉산더 듀드니(A.K.Dewdney)의 또다른 주장은 신경망은 비행기의 자동운전모드[41] 또는 신용카드 사기 탐지 같은 여러 가지 복잡하고 다양한 문제를 효과적이고 성공적으로 해결해왔다는 것이다.
하지만, 기술 집필자 로저 브리드만(Roger Bridgman)은 듀드니의 신경망에 대한 주장에 대해 이러한 말을 남겼다.
"신경망은 예를 들면, 그것은 더 높은 목적을 달성할 수 있다고 과장된 광고를 하고 있을 뿐만 아니라 이것이 어떻게 동작하는지 이해도 하지 않고도 성공적인 네트워크를 만들어 낼 수 있다고 말하는데, 이것은 불투명하고 이해할 수 없는 것일 뿐만 아니라 과학적 측면에서 가치가 없는 것이다."
그의 이러한 과학(인공신경망)은 기술이 아니라는 강한 발표에도, 듀드니는 "이것은 단지 남들이 보는 앞에서 그들이 이것을 이해하지 못하더라도 훌륭한 기술자들인 것처럼 보이기 위해 신경망을 안 좋은 학문이라고 비판하는 것"이라고 했다. 불투명하고 이해할 수 없는 것이라도 유용한 기계가 될 수있다면 그것은 여전히 우리에게 가치있는 것이고 필요한 것일 것이다.[42] .
비록 인공 신경망을 배우고 이해하고 분석하는 것이 매우 힘든 일이라는 것은 사실이지만, 실제 생물에서의 신경망을 배우고 이해하여 분석해서 적용하는 것보다는 훨씬 쉬운 일일 것이다. 게다가, 신경망을 구현하는 학습 알고리즘을 연구하는 연구자들은 점진적으로 기계학습을 성공적으로 하게 할 수 있는 신경 유전적 원리를 발견해 내는데 성공하고 있다. 예를 들어, 벤지오(Bengio)와 레쿤(LeCun)이 2007년에 쓴 논문에서는, 지역 vs 비지역 학습(local vs non-local learning)과 얕은 vs 깊은 구조(shallow vs deep architecture)에 대해서 다루고 있다[43].
혼합적 접근[편집]
일부 다른 분석가들은 신경망과 다른 분야에 대한 혼합적 모델을 지지한다.(예를 들면 기호적 접근과 인공신경망의 결합) 이러한 두 가지 접근방식의 내부 혼합은 사람의 내적 동작에 대한 메커니즘을 조금 더 잘 잡아 낼 수 있을 것이라 생각하기 때문이다.[44][45]
갤러리[편집]
-
단일 층의 전방전파 인공신경망이다. p개의 네트워크로의 입력과 q개의 네트워크에서의 출력이 존재한다. 에서의 전파는 그림을 명료하게 하기 위해 생략되었다. 이 신경망에서, q번째 출력값 은, 로 계산될 수 있다.
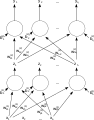
-
두개 층의 전방전파 인공신경망이다.
같이 보기[편집]
- 인공생명
- 결정 트리
- 전문가 시스템
- 퍼지 논리
- 유전 알고리즘
- 신경망
- 신경망 소프트웨어
- 광학 신경망
- 입자 군 최적화
- 회귀 분석
- 담금질 기법(simulated annealing)
- 교사 학습
- 로지스틱 회귀
- 딥 러닝
- 지도 학습
- 뉴럴 디자이너
각주[편집]
- ↑ McCulloch, Warren; Walter Pitts (1943). “A Logical Calculus of Ideas Immanent in Nervous Activity”. 《Bulletin of Mathematical Biophysics》 5 (4): 115–133. doi:10.1007/BF02478259.
- ↑ Hebb, Donald (1949). 《The Organization of Behavior》. New York: Wiley.
- ↑ Farley, B.G.; W.A. Clark (1954). “Simulation of Self-Organizing Systems by Digital Computer”. 《IRE Transactions on Information Theory》 4 (4): 76–84. doi:10.1109/TIT.1954.1057468.
- ↑ Rochester, N.; Holland, J.H.; Habit, L.H; Duda, W.L (1956). “Tests on a cell assembly theory of the action of the brain, using a large digital computer”. 《IRE Transactions on Information Theory》 2 (3): 80–93. doi:10.1109/TIT.1956.1056810.
- ↑ Rosenblatt, F. (1958). “The Perceptron: A Probabilistic Model For Information Storage And Organization In The Brain”. 《Psychological Review》 65 (6): 386–408. doi:10.1037/h0042519. PMID 13602029.
- ↑ Werbos, P.J. (1975). 《Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences》.
- ↑ Minsky, M.; S. Papert (1969). 《An Introduction to Computational Geometry》. MIT Press. ISBN 0-262-63022-2.
- ↑ Rumelhart, D.E; James McClelland (1986). 《Parallel Distributed Processing: Explorations in the Microstructure of Cognition》. Cambridge: MIT Press.
- ↑ Russell, Ingrid. “Neural Networks Module”. 2014년 5월 29일에 원본 문서에서 보존된 문서. 2012에 확인함.
- ↑ Yang, J. J.; Pickett, M. D.; Li, X. M.; Ohlberg, D. A. A.; Stewart, D. R.; Williams, R. S. Nat. Nanotechnol. 2008, 3, 429–433.
- ↑ Strukov, D. B.; Snider, G. S.; Stewart, D. R.; Williams, R. S. Nature 2008, 453, 80–83.
- ↑ 2012 Kurzweil AI Interview Archived 2018년 8월 31일 - 웨이백 머신 with Jürgen Schmidhuber on the eight competitions won by his Deep Learning team 2009–2012
- ↑ http://www.kurzweilai.net/how-bio-inspired-deep-learning-keeps-winning-competitions Archived 2018년 8월 31일 - 웨이백 머신 2012 Kurzweil AI Interview with Jürgen Schmidhuber on the eight competitions won by his Deep Learning team 2009–2012
- ↑ Graves, Alex; and Schmidhuber, Jürgen; Offline Handwriting Recognition with Multidimensional Recurrent Neural Networks, in Bengio, Yoshua; Schuurmans, Dale; Lafferty, John; Williams, Chris K. I.; and Culotta, Aron (eds.), Advances in Neural Information Processing Systems 22 (NIPS'22), 7–10 December 2009, Vancouver, BC, Neural Information Processing Systems (NIPS) Foundation, 2009, pp. 545–552.
- ↑ A. Graves, M. Liwicki, S. Fernandez, R. Bertolami, H. Bunke, J. Schmidhuber. A Novel Connectionist System for Improved Unconstrained Handwriting Recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 31, no. 5, 2009.
- ↑ Graves, Alex; and Schmidhuber, Jürgen; Offline Handwriting Recognition with Multidimensional Recurrent Neural Networks, in Bengio, Yoshua; Schuurmans, Dale; Lafferty, John; Williams, Chris K. I.; and Culotta, Aron (eds.), Advances in Neural Information Processing Systems 22 (NIPS'22), December 7th–10th, 2009, Vancouver, BC, Neural Information Processing Systems (NIPS) Foundation, 2009, pp. 545–552
- ↑ A. Graves, M. Liwicki, S. Fernandez, R. Bertolami, H. Bunke, J. Schmidhuber. A Novel Connectionist System for Improved Unconstrained Handwriting Recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 31, no. 5, 2009.
- ↑ 가 나 D. C. Ciresan, U. Meier, J. Masci, J. Schmidhuber. Multi-Column Deep Neural Network for Traffic Sign Classification. Neural Networks, 2012.
- ↑ D. Ciresan, A. Giusti, L. Gambardella, J. Schmidhuber. Deep Neural Networks Segment Neuronal Membranes in Electron Microscopy Images. In Advances in Neural Information Processing Systems (NIPS 2012), Lake Tahoe, 2012.
- ↑ D. C. Ciresan, U. Meier, J. Schmidhuber. Multi-column Deep Neural Networks for Image Classification. IEEE Conf. on Computer Vision and Pattern Recognition CVPR 2012.
- ↑ Fukushima, K. (1980). “Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position”. 《Biological Cybernetics》 36 (4): 93–202. doi:10.1007/BF00344251. PMID 7370364.
- ↑ M Riesenhuber, T Poggio. Hierarchical models of object recognition in cortex. Nature neuroscience, 1999.
- ↑ Deep belief networks at Scholarpedia.
- ↑ Hinton, G. E.; Osindero, S.; Teh, Y. W. (2006). “A Fast Learning Algorithm for Deep Belief Nets” (PDF). 《Neural Computation》 18 (7): 1527–1554. doi:10.1162/neco.2006.18.7.1527. PMID 16764513.
- ↑ John Markoff (2012년 11월 23일). “Scientists See Promise in Deep-Learning Programs”. 《New York Times》.
- ↑ “The Machine Learning Dictionary”. 2018년 8월 26일에 원본 문서에서 보존된 문서. 2015년 4월 28일에 확인함.
- ↑ Dominic, S., Das, R., Whitley, D., Anderson, C. (July 1991). 〈Genetic reinforcement learning for neural networks〉. 《IJCNN-91-Seattle International Joint Conference on Neural Networks》. IJCNN-91-Seattle International Joint Conference on Neural Networks. Seattle, Washington, USA: IEEE. doi:10.1109/IJCNN.1991.155315. ISBN 0-7803-0164-1. 2012년 7월 29일에 확인함.
- ↑ Hoskins, J.C.; Himmelblau, D.M. (1992). “Process control via artificial neural networks and reinforcement learning”. 《Computers & Chemical Engineering》 16 (4): 241–251. doi:10.1016/0098-1354(92)80045-B.
- ↑ Bertsekas, D.P., Tsitsiklis, J.N. (1996). 《Neuro-dynamic programming》. Athena Scientific. 512쪽. ISBN 1-886529-10-8.
- ↑ Secomandi, Nicola (2000). “Comparing neuro-dynamic programming algorithms for the vehicle routing problem with stochastic demands”. 《Computers & Operations Research》 27 (11–12): 1201–1225. doi:10.1016/S0305-0548(99)00146-X.
- ↑ de Rigo, D., Rizzoli, A. E., Soncini-Sessa, R., Weber, E., Zenesi, P. (2001). 〈Neuro-dynamic programming for the efficient management of reservoir networks〉 (PDF). 《Proceedings of MODSIM 2001, International Congress on Modelling and Simulation》. MODSIM 2001, International Congress on Modelling and Simulation. Canberra, Australia: Modelling and Simulation Society of Australia and New Zealand. doi:10.5281/zenodo.7481. ISBN 0-867405252. 2012년 7월 29일에 확인함.
- ↑ Damas, M., Salmeron, M., Diaz, A., Ortega, J., Prieto, A., Olivares, G. (2000). 〈Genetic algorithms and neuro-dynamic programming: application to water supply networks〉. 《Proceedings of 2000 Congress on Evolutionary Computation》. 2000 Congress on Evolutionary Computation. La Jolla, California, USA: IEEE. doi:10.1109/CEC.2000.870269. ISBN 0-7803-6375-2. 2012년 7월 29일에 확인함.
- ↑ Deng, Geng; Ferris, M.C. (2008). “Neuro-dynamic programming for fractionated radiotherapy planning”. 《Springer Optimization and Its Applications》 12: 47–70. doi:10.1007/978-0-387-73299-2_3.
- ↑ de Rigo, D., Castelletti, A., Rizzoli, A.E., Soncini-Sessa, R., Weber, E. (January 2005). 〈A selective improvement technique for fastening Neuro-Dynamic Programming in Water Resources Network Management〉. Pavel Zítek. 《Proceedings of the 16th IFAC World Congress – IFAC-PapersOnLine》. 16th IFAC World Congress. Prague, Czech Republic: IFAC. doi:10.3182/20050703-6-CZ-1902.02172. ISBN 978-3-902661-75-3. 2011년 12월 30일에 확인함.
- ↑ Ferreira, C. (2006). “Designing Neural Networks Using Gene Expression Programming” (PDF). In A. Abraham, B. de Baets, M. Köppen, and B. Nickolay, eds., Applied Soft Computing Technologies: The Challenge of Complexity, pages 517–536, Springer-Verlag.
- ↑ Da, Y., Xiurun, G. (July 2005). T. Villmann, 편집. 《An improved PSO-based ANN with simulated annealing technique》. New Aspects in Neurocomputing: 11th European Symposium on Artificial Neural Networks. Elsevier. doi:10.1016/j.neucom.2004.07.002. 2012년 4월 25일에 원본
|보존url=은|url=을 필요로 함 (도움말)에서 보존된 문서. - ↑ Wu, J., Chen, E. (May 2009). Wang, H., Shen, Y., Huang, T., Zeng, Z., 편집. 《A Novel Nonparametric Regression Ensemble for Rainfall Forecasting Using Particle Swarm Optimization Technique Coupled with Artificial Neural Network》. 6th International Symposium on Neural Networks, ISNN 2009. Springer. doi:10.1007/978-3-642-01513-7_6. ISBN 978-3-642-01215-0. 2014년 12월 31일에 원본
|보존url=은|url=을 필요로 함 (도움말)에서 보존된 문서. - ↑ Ganesan, N. “Application of Neural Networks in Diagnosing Cancer Disease Using Demographic Data” (PDF). International Journal of Computer Applications.
- ↑ Siegelmann, H.T.; Sontag, E.D. (1991). “Turing computability with neural nets” (PDF). 《Appl. Math. Lett.》 4 (6): 77–80. doi:10.1016/0893-9659(91)90080-F. 2013년 5월 2일에 원본 문서 (PDF)에서 보존된 문서. 2013년 12월 9일에 확인함.
- ↑ Balcázar, José (Jul 1997). “Computational Power of Neural Networks: A Kolmogorov Complexity Characterization”. 《Information Theory, IEEE Transactions on》 43 (4): 1175–1183. doi:10.1109/18.605580. 2014년 11월 3일에 확인함.
- ↑ NASA - Dryden Flight Research Center - News Room: News Releases: NASA NEURAL NETWORK PROJECT PASSES MILESTONE. Nasa.gov. Retrieved on 2013-11-20.
- ↑ “Roger Bridgman's defence of neural networks”. 2012년 3월 19일에 원본 문서에서 보존된 문서. 2015년 4월 30일에 확인함.
- ↑ “보관된 사본”. 2015년 5월 15일에 원본 문서에서 보존된 문서. 2015년 4월 30일에 확인함.
- ↑ Sun and Bookman (1990)
- ↑ Tahmasebi; Hezarkhani (2012). “A hybrid neural networks-fuzzy logic-genetic algorithm for grade estimation”. 《Computers & Geosciences》 42: 18–27. doi:10.1016/j.cageo.2012.02.004.


























![{\displaystyle \textstyle C=E\left[(f(x)-y)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53d492067dfb4b20e428a37d76787463e95c8d18)




![{\displaystyle \textstyle C=E[(x-f(x))^{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2929ecb1606fdfeaddc55477d9671e11c034e21c)