선형 회귀
| 기계 학습과 데이터 마이닝 |
|---|
 |

통계학에서 선형 회귀(線型回歸, 영어: linear regression)는 종속 변수 y와 한 개 이상의 독립 변수 (또는 설명 변수) X와의 선형 상관 관계를 모델링하는 회귀분석 기법이다. 한 개의 설명 변수에 기반한 경우에는 단순 선형 회귀(simple linear regression), 둘 이상의 설명 변수에 기반한 경우에는 다중 선형 회귀라고 한다.[참고 1]
선형 회귀는 선형 예측 함수를 사용해 회귀식을 모델링하며, 알려지지 않은 파라미터는 데이터로부터 추정한다. 이렇게 만들어진 회귀식을 선형 모델이라고 한다.
선형 회귀는 깊이있게 연구되고 널리 사용된 첫 번째 회귀분석 기법이다.[3] 이는 알려지지 않은 파라미터에 대해 선형 관계를 갖는 모델을 세우는 것이, 비선형 관계를 갖는 모델을 세우는 것보다 용이하기 때문이다.
선형 회귀는 여러 사용 사례가 있지만, 대개 아래와 같은 두 가지 분류 중 하나로 요약할 수 있다.
- 값을 예측하는 것이 목적일 경우, 선형 회귀를 사용해 데이터에 적합한 예측 모형을 개발한다. 개발한 선형 회귀식을 사용해 y가 없는 x값에 대해 y를 예측하기 위해 사용할 수 있다.
- 종속 변수 y와 이것과 연관된 독립 변수 X1, ..., Xp가 존재하는 경우에, 선형 회귀 분석을 사용해 Xj와 y의 관계를 정량화할 수 있다. Xj는 y와 전혀 관계가 없을 수도 있고, 추가적인 정보를 제공하는 변수일 수도 있다.
일반적으로 최소제곱법(least square method)을 사용해 선형 회귀 모델을 세운다. 최소제곱법 외에 다른 기법으로도 선형 회귀 모델을 세울 수 있다. 손실 함수(loss fuction)를 최소화하는 방식으로 선형 회귀 모델을 세울 수도 있다. 최소제곱법은 선형 회귀 모델 뿐 아니라, 비선형 회귀 모델에도 적용할 수 있다. 최소제곱법과 선형 회귀는 가깝게 연관되어 있지만, 그렇다고 해서 동의어는 아니다.
선형 회귀에 대한 소개[편집]
선형 회귀는 주어진 데이터 집합 에 대해, 종속 변수 yi와 p개의 설명 변수 xi 사이의 선형 관계를 모델링한다. 모델은 다음과 같은 형태를 갖는다.
주어진 식에서 는 각 독립변수의 계수이며, 는 선형 회귀로 추정되는 모수의 개수이다. T는 전치를 의미하고, xiTβ는 xi와 β의 내적을 의미한다. 는 오차항, 오차 변수로, 관찰되지 않은 확률 변수이며, 종속 변수와 독립 변수 사이에 오차를 의미한다.
이것이 선형 회귀라 불리는 것은, 종속변수가 독립변수에 대해 선형 함수(1차 함수)의 관계에 있을 것이라 가정하기 때문이다. 그러나 의 그래프가 직선이고 가 의 선형 함수일 것이라고 생각하는 것은 잘못이다. 예를 들어 다음과 같은 "선형 회귀"도 있기 때문이다. 는 와 에 관해 선형이기 때문에, x축과 y축을 가진 그래프가 직선상에 있지 않더라도 선형회귀라고 할 수 있다.
이 식은 벡터 형식으로 표현하면 다음과 같이 표현할 수 있다.
이 식에서 각 항의 의미는 다음과 같다.
몇 가지 중요한 용어를 확인하고 넘어가자.
- 는 응답 변수, 종속 변수라 불린다 (독립 변수와 종속 변수 읽어보기.) 어떤 변수가 종속 변수가 되고, 어떤 변수가 독립 변수가 되는지는, 어떤 변수가 무엇에 직간접적으로 영향을 주느냐에 대한 가정을 따른다. 한편, 목적에 따라서는 의존 관계에 대한 뚜렷한 이유없이 한 변수가 다른 변수에 종속하는 것으로 가정하고 선형 회귀 분석을 하기도 한다.
- 는 입력 변수, 예측 변수, 독립 변수라 불린다 (독립 변수와 종속 변수 읽어보기. 독립 변수는 독립 확률 변수와는 다른 것이다.) 행렬 는 설계 행렬이라 불리기도 한다.
- 일반적으로 입력 변수에 상수가 포함된다. 예를 들어, xi1를 상수로 택한다 ( = 1 i = 1, ..., n) xi1 앞에 붙는 상수 β를 절편이라 부른다. 많은 선형 통계 모델에서 절편이 필요하며, 실질적으로 절편이 0인 경우에도 이를 포함해 모델링한다.
- 때로 독립 변수는 다른 독립 변수 또는 데이터에 대해 비선형 함수이기도 하다. 이러한 경우에도 이 독립 변수가 파라미터 벡터 β에 대해서만 선형이기만 하면 여전히 선형 모델이라 부른다.
- 독립 변수 xij는 확률 변수로 생각할 수도 있고, 또는 고정된 값으로 생각할 수도 있다. 경우에 따라 두 가지 중에 적합한 것을 선택해야 하지만, 두 가지 모두 같은 추정 과정을 거친다. 하지만 각각의 경우에서 해석은 다르다.
- 는 p차원 파라미터 벡터이다. 이것의 각 원소는 회귀 계수라고 불리기도 한다. 파라미터 벡터의 원소는 종속 변수에 대한 편미분으로 해석할 수도 있다.
- 는 오차항, 노이즈이다. 이 변수는 종속 변수 yi에 대한 모든 오차 요인을 포함한다.
예제. 작은 공을 던져 올리고, 그것의 높이 hi를 시간 ti에서 측정한다고 하자. 이를 수식으로 표현하면 다음과 같다.

이 식에서 β1는 공의 초기 속도이며, β2는 중력에 비례하는 계수이다. εi는 측정 오차를 의미한다. 선형 회귀는 측정한 데이터를 사용해 β1과 β2를 추정할 때 사용할 수 있다. 이렇게 세워진 모델은 시간 변수에 대해서는 비선형이지만, 파라미터 β1와 β2에 대해서는 선형이다. 만약 독립 변수를 다음과 같이 표현하면, xi = (xi1, xi2) = (ti, ti2), 식을 다음과 같이 쓸 수 있다.
선형 회귀에서의 가정[편집]
표준 선형 회귀 분석 모델에서는 예측 변수, 응답 변수 그리고 그 사이의 관계에 대해 다양한 가정을 한다. 확장된 선형 회귀 분석에서는 이러한 가정을 완화하기도 하고, 때로는 가정을 제거하기도 한다. 일반적으로 확장된 선형 회귀는 추정 과정을 더 복잡하게 하거나 시간을 더 많이 소모한다. 정확한 모델을 세우기 위해 더 많은 데이터가 요구하기도 한다. 표준 선형 회귀에서의 대표적인 가정들은 다음과 같다.
- 약한 외생성. 설명 변수 x를 확률 변수가 아니라, 고정된 값으로 취급한다. 이는 설명 변수가 에러가 없음을 의미한다. 측정 오차로 인해 설명 변수가 오염되지 않았음을 가정하는 것과 같다. 이러한 가정이 현실적이지 않지만, 이 가정을 제외하면 설명 변수에 오차를 포함한 모델을 세워야 한다.
- 선형성. 응답 변수가 예측 변수와 선형 회귀 계수의 선형 조합으로 표현 가능함을 의미한다. 이는 생각보다 까다롭지 않은 가정인데, 이것은 파라미터에 대한 선형성만 가정하기 때문이다. 예측 변수는 임의로 변형될 수도 있고, 동일한 예측 변수가 더해질 수도 있고, 하나를 다르게 변형할 수도 있다. 이러한 기법이 실제로 다항 회귀에 사용된다. 응답 변수를 예측 변수에 대한 임의의 다항 함수로 모델링한다. 이는 선형 회귀를 매우 강력하게 만든다. 실제로 이러한 다항 회귀는 때로 너무 강력해서, 모델이 데이터에 과적합(overfit)하게 되기도 한다. 이를 방지하기 위해 일종의 정규화 기법을 사용할 수도 있다. 이를 적용한 예로는 능형 회귀분석(ridge regression) 또는 Lasso 회귀 등이 있다. 베이지안 선형 회귀 또한 사용할 수 있는데, 베이지안 선형 회귀는 근본적으로 과적합을 방지하는 효과를 갖는다.
- 상수 분산 (즉, 동분산성). 이는 서로 다른 응답 변수들의 오차가 설명 변수와 무관하게 항상 같은 분산을 가짐을 의미한다. 실제로는 이러한 가정은 타당하지 않다. 응답 변수들의 오차가 같은 분산을 갖지 않으며, 오차의 분산은 설명 변수에 영향을 받는다.
- 오차의 독립성. 독립 변수의 오차가 서로 무관함을 가정한다. 일부 선형 회귀 기법은 상관된 오차를 다룰 수 있지만, 정규화가 적용되지 않은 상황에서는 더 많은 데이터를 필요로 한다. 베이지안 선형 회귀가 이러한 문제를 다루는 일반적인 기법이다.
- 예측 변수에서의 다중공선성의 부재. 표준 최소제곱법 추정 기법에서, 설계 행렬 X는 반드시 전열계수 p를 갖는다. 그렇지 않으면, 예측 변수 사이에 다중공선성이 생긴다. 이는 두 개 이상의 상관된 예측 변수로 인해 발생한다. 또한, 추정하고자 하는 파라미터에 비해 데이터가 너무 적어도 발생할 수 있다. 다중공선성이 발생하면, 파라미터 벡터 β는 유일한 해를 갖지 않게 된다. 다중공선성이 있는 상황에서도 선형 회귀 모델을 만들 수 있는 기법이 개발되긴 했으나, 몇 가지 추가적인 가정이 필요하다.
선형 회귀의 해석[편집]

예측 변수에 대한 모든 값이 주어졌을 때, 수립한 선형 회귀 모델을 사용해 예측 변수 xj가 응답 변수 y에 미치는 영향을 확인할 수 있다. βj는 xj가 한 단위 변했을 때, y의 기대 변화량을 의미한다. 이는 때로 y에 대한 xj의 고유 영향이라 불리기도 한다. 반면에, y에 대한 xj의 한계 효과는 xj와 y 사이의 Pearson 상관 계수 또는 선형 회귀를 사용해 평가할 수 있다. 회귀 결과를 해석할 때 주의해야 하는데, 일부 독립 변수가 응답 변수의 변화에 영향을 주지 않을 수 있기 때문이다 (무의미한 독립 변수일 수도 있고, y 절편에 해당할 수도 있기 때문이다.) 회귀 결과를 해석할 때 주의해야 하는데, 한계 효과가 큰 상황에서도 고유 영향은 적을 수 있기 때문이다. 반면에 한계 효과는 적은데 고유 영향이 큰 상황이 있을 수도 있다. 아주 복잡하게 서로 연계되어 있는 시스템을 분석하는 상황에서 고유 효과는 매우 중요한 역할을 한다. 경우에 따라 이는 예측 변수에 영향을 주기도 한다. 하지만, 많은 경우에 다중 선형 회귀는 응답 변수와 예측 변수 사이의 관계를 밝히는 것에 실패한다. 공통점 분석은 이러한 상관 관계를 해석하는 것에 도움을 준다.
손실 함수[편집]
- 단순 선형 회귀의 손실 함수.
- 관측된 m개의 데이터 에 대하여 단순 선형 회귀 모델을 다음과 같이 정의할 때,
- 손실 함수 는 아래와 같이 정의할 수 있다.
- 다변량 선형 회귀의 손실 함수.
- n개의 독립 변수 X와 관측된 m개의 데이터에 대하여 다변량 선형 회귀 모델을 다음과 같이 정의할 때,
- 손실 함수 는 아래와 같이 정의할 수 있다.
선형 회귀 기법의 확장[편집]
선형 회귀를 확장한 다양한 기법들이 개발되었으며, 각각은 서로 다른 가정을 갖고 있거나, 기본 모델에서 가정을 완화하기도 한다.
단순 선형 회귀와 다중 선형 회귀[편집]
선형 회귀의 가장 단순한 예제는 한 개의 스칼라 독립 변수 x와 한 개의 스칼라 의존 변수 y의 관계일 것이다. 이를 단순 선형 회귀라 부른다. 여기에서 독립 변수를 여러 개로 확장한 것이 다중 선형 회귀이다. 실세계의 거의 대부분의 문제는 여러 개의 독립 변수를 포함하며, 선형 회귀라 함은 보통 다중 선형 회귀를 일컫는다. 하지만 이러한 경우에도 여전히 응답 변수 y는 한 개의 스칼라 변수이다. 다변량 선형 회귀는 응답 변수 y가 벡터인 경우를 의미한다. 이러한 경우를 일반 선형 회귀라 부른다. 다중 선형 회귀와 다변량 선형 회귀는 다른 의미이므로, 혼동하지 않도록 주의해야 한다.
일반 회귀 모델[편집]
일반 회귀 모델은 응답 변수 Y가 스칼라가 아니라 벡터인 경우를 대상으로 한다. 조건부 선형성 E(y|x) = Bx은 여전히 유지된다 (행렬 B는 β를 행렬로 표현한 것). 일반 회귀 모델은 다변량 회귀 모델과 동일하다. 다변량 회귀 모델은 다중 선형 회귀와는 반드시 구분해야 한다. 다변량 회귀 모델은 일반 회귀 모델을 의미하고, 다중 선형 회귀는 여러 개의 선형 모델을 의미한다.
이분산 회귀 모델[편집]
이분산성을 허용하기 위해 다양한 회귀 모델이 개발되었다. 응답 변수들의 오차의 분산이 서로 다른 것을 허용한다. 가중 최소 제곱법은 응답 변수의 오차가 서로 다른 분산을 갖거나, 연관된 경우에도 선형 회귀 모델을 수립할 수 있게 허용한다. 이분산성 일치 표준 에러 기법은 더 개선된 기법으로, 오차가 서로 연관되어 있지는 않지만 서로 다른 분산을 갖는 경우에 선형 회귀 모델을 수립할 수 있다.
계층적 선형 모델[편집]
계층적 선형 모델은 데이터가 여러겹으로 회귀되는 경우에 이용할 수 있다. 다시 말해 A가 B로 회귀되고, B가 C로 회귀 되는 구조를 말한다. 이러한 구조는 일상 생활에서 흔히 볼 수 있는데, 가령 학생은 학급에 속하고, 학급은 학년에 속하며 학년은 학교에 속하는 경우를 들 수 있다. 이런 경우 학생의 응답 변수로 시험 성적을 이용 한다면 학급, 학년, 학교에 대해 각각 다른 공변을 얻을 수 있다.
오차 변수 모델[편집]
오차 변수 모델(errors-in-variables) 은 (또는 "오차 측정 모델") 기존의 선형 회귀 모델에서 독립 변수 X가 오차와 같이 관측될 수 있도록 확장한 것이다. 이 오차는 β의 표준 추정량이 편향되는데 원인이 된다. 일반적으로는 이 영향은 0에 가깝게 편향된다.
그 외[편집]
- Dempster–Shafer theory에서, 특히 linear belief function에서, 선형 회귀 모델은 부분적으로 sweep 함수를 적용한 행렬로 표현될 수 있다. 이 행렬은 관측된 값과 표준 분포를 따르는 어떤 값으로 이루어진다. sweep 함수를 적용한 행렬이나 그렇지 않은 행렬들의 구성은 선형 회귀 모델을 추정하는 대안을 제공한다.
선형 회귀 모델 추정 기법[편집]
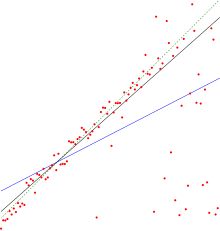
선형 회귀에서 파라미터 추정을 위해 다양한 기법들이 개발되었다. 각각의 기법들은 알고리즘의 연산 복잡도, 닫힌 형태의 해법 존재 여부, 데이터의 분포에 대한 가정, 변수의 관계에 대한 이론적 가정 등이 다르다. 아래에서는 일반적인 선형 회귀 추정 기법에 대해 설명하고자 한다.
최소제곱법[편집]
Ordinary least squares[편집]
- (OLS)는 가장 단순하고 많이 쓰이는 추정 방법이다. 이는 개념적으로 단순하고, 계산이 간단하다. OLS 추정은 일반적으로 실험이나 관측치에 적용하고자 할 때 사용한다. OLS 기법은 오차의 제곱의 합을 최소화하는 기법으로, 추정하고자 하는 파라미터 β에 대한 표현식을 다음과 같이 구할 수 있다.
- 오차가 유한한 분산을 가지며, 오차가 독립 변수와 연관되어 있지 않다면, 추정은 편향되어있지 않고, 일관성 있다.
Generalized least squares (GLS)[편집]
- (GLS)는 OLS를 확장한 방법으로, 모델의 오차들간에 이분산이나 상관성, 혹은 두 성질 모두 가질때 β를 더 효율적으로 예측할 수 있다. (이분산성이나 상관성의 형태는 데이터에 독립적이어야 한다.) 오차들이 서로 상관성이 없을 때 이분산성을 다루기 위해서 GLS는 OLS 회귀 결과로부터 잔차 제곱의 합으로가중치를 최소화한다. 이 때, i번째 가중치는 var(εi)에 반비례한다. 이러한 GLS의 특별한 케이스를 "weighted least squares"라고 부른다. 추정 문제에 대한 GLS 솔루션은
- Ω 가 오차에 대한 공분산 행렬일 때,
- GLS는 데이터를 선형 변환하여 OLS에서의 가정들이 변형된 데이터에 만족하도록 한 것으로 볼 수 있다. GLS를 사용하려면 오차의 공분산 구조가 곱셈법 상수로 알려져야 한다.
Percentage least squares[편집]
- 는 오차의 퍼센트를 줄이는 방법으로 예측하거나 시계열 데이터를 분석하는 분야에서 유용하게 쓰인다. OLS를 사용하면 상한선에서 큰 잔차가 우세한 값을 갖는 경우에, 종속 변수가 상수 분산을 가지지 않고 넓은 범위를 가질 때 유용하게 쓰인다. 오차의 퍼센티지나 상대 값이 표준 분포를 따를 때, percentage least squares 회귀 기법은 최대 가능도 추정을 제공한다. OLS는 가법 오차 모형과 관련있는 반면에 이 회귀 기법은 승법 오차 모형과 관련있다.[4]
Iteratively reweighted least squares (IRLS)[편집]
- IRLS는 모델들의 오차들간에 이분산성이나 상관성이 존재하지만 공분산 구조가 거의 알려지지 않을 때 사용된다.[5] 첫 번째 반복문에서 임시의 공분산 구조를 가진 OLS나 GLS가 실행되고 잔차가 구해진다. 이때 구해진 잔차를 바탕으로 오차의 공분산 구조의 향상된 추정치를 구할 수 있다. 이 오차 구조의 추정치를 사용하여 GLS를 실행하여 가중치를 구한다. 이 과정은 반복되어 수렴된 값을 얻을 수 있지만 대부분의 경우에서 한 번의 반복문으로 효율적인 추정치 β를 구할 수 있다.[6][7]
Instrumental variables[편집]
- IV 회귀 기법은 입력 변수가 오차와 상관성이 있을 때 사용된다. 이러한 경우에서 우리는 E[ziεi] = 0를 만족시키는 부가적인 instrumental variables zi 가 필요하다. 만약 Z가 행렬 형태의 instrument라면 추정량은 아래의 식과 같이 닫힌 형태로 주어진다.
Optimal instruments[편집]
- 이 회귀 기법은 전형적인 IV 회귀 기법을 확장한 것으로 E[εi|zi] = 0를 만족시키는 경우에 사용된다.
Total least squares (TLS)[편집]
- (TLS)[8]는 OLS보다 더 기하학적으로 대칭된 방법으로 독립 변수와 종속 변수를 다루는 최소 제곱 추청 기법이다. 오차 변수 문제를 해결하는 한 방법으로 때때로 독립 변수에 오차가 없다고 가정될 때 사용된다.
최대가능도방법[편집]
최대 가능도 추정 (MLE : Maximum likelihood estimation )[편집]
- 다음과 같은 로그 가능도 함수를 구할 수 있다
- 위 식의 음수를 취한 음 로그 가능도 함수(NLL : negative log likelihood)는 아래와 같다
- NLL의 최솟값을 구하기 위해서는 위식에서 아래의 부분을 최소화 하면 된다
- 위 식은 잔차제곱합(RSS : Residual Sum of Squares)이며, 이를 통해 최적의 을 구할 수 있다.
능형 회귀 분석(Ridge regression)[편집]
- 최대 사후 확률(MAP) 을 구하기 위한 식은,
- 최대 사후 확률을 추정하는 문제를 해결하기 위해서는 다음식 최솟값을 구하면 된다
- 최대가능도추정의 음로그가능도함수(NLL)과 비교시 첫 번째 식은 NLL 과 동일하고, 두 번째 식은 복잡도 제약조건을 고려한다
최소 절대 편차[편집]
- 최소 절대 편차(least absolute deviation, LAD) 방식은 이상치(outlier)가 존재하는 상황에서 OLS보다 이상치에 대해 덜 민감하게 반응하는 방법이다(단, 이상치가 존재하지 않은 상황에서는 OLS보다 비효율적이다) . 이것은 라플라스 모델의 최대가능도추정(Maximun Likelihood Estimation)과 동일하다.[9]
적응 추정(Adaptive estimation)[편집]
- 오차항이 회귀값 으로부터 독립이라고 가정할때, 최적 검출기는 첫 번째 단계가 오차항의 분포에 대한 비모수 추정을 하는 2단계의 MLE로 얻을 수 있다.[10]
선형 회귀 추정 기법[편집]
- Bayesian linear regression
- Quantile regression
- Mixed models
- Principal component regression (PCR)
- Least-angle regression
- The Theil–Sen estimator
선형 회귀의 응용[편집]
생물학, 행동학, 경제학 및 기타 사회과학에서 변수들 사이의 관계를 설명하고자 할 때, 선형 회귀를 사용한다. 예를 들어, 추세 분석·역학 조사·재무 관리·경제학에 응용된다.
추세 분석[편집]
추세선은 데이터를 시간 축으로 놓고 봤을 때, 데이터의 값이 장기적으로 어떻게 변하는지 직선으로 표현한 것이다. 추세선은 특정 데이터 집합(GDP, 원유 가격 또는 주식 가격 등)에서 값이 증가세에 있는지 감소세에 있는지 보여준다. 이러한 데이터의 추세는 데이터를 눈으로 확인하는 것만으로도 추정 가능하지만, 더 정확하게는 선형 회귀를 사용해 추세선을 그릴 수 있다. 추세선은 일반적으로 직선이며, 경우에 따라 더 높은 차수의 곡선을 사용하기도 한다. 때로는 경영 분석에서 시간에 따른 데이터 변화를 보고자 추세선을 사용하기도 한다. 추세선을 사용하면 특정 사건이 값에 미치는 영향을 매우 간단하게 확인할 수 있다. 추세선을 그리는 것은 대조군이 필요하지도 않고, 실험 설계가 필요하지도 않으며 간단하다는 장점이 있다. 하지만 과학적인 검증이 부족해, 예상한 것 이외의 요인이 잠재적으로 데이터에 미치는 영향은 놓칠 수 있다.
역학 조사[편집]
흡연률과 사망률, 유병률을 연관이 있다는 증거는 회귀 분석을 적용한 관찰 연구에서 확인되었다. 관찰한 데이터에서 확신할 수 없는 상관 관계를 제거하기 위해, 연구자들은 일반적으로 실제로 관심있는 변수 외에도 여러 개의 변수를 삽입해 회귀 분석 모델을 수립한다. 예를 들어, 흡연률과 수명의 상관관계를 보고싶다고 하자. 연구자들은 실제로 관심있는 독립 변수인 흡연률 외에도 사회경제적 조건 등을 독립 변수에 추가적로 삽입해, 사회경제적 조건이 수명과 연관이 있는지 확인하곤 한다. 하지만 모든 가능한 변수를 추가할 수는 없으므로, 랜덤 통제 실험을 통해 상관관계를 조사하기도 한다.
재무 관리[편집]
자본자산 가격결정 모형에서 체계적 위험을 베타에 대한 선형 회귀로 표현한다.
경제학[편집]
선형 회귀는 경제학에서 경험적인 데이터를 통해 미래를 예측하고자 할 때 주로 사용된다. 비용 예측[11], 고정 투자 예측, 재고 관리 예측, 필요 유동 자산 예측[12], 노동 수요 예측[13], 노동 공급 예측[13] 등에 선형 회귀를 사용할 수 있다.
환경 과학[편집]
선형 회귀는 환경 과학에도 적용할 수 있다. 캐나다의 환경 영향 모니터링 프로그램에서는 제지 공장과 광산이 수질에 미치는 영향을 조사하기 위해 물고기와 수질에 대해 선형 회귀를 사용하기도 했다.[14]
선형회귀 방정식[편집]

선형회귀방정식 을 얻을 때 을 조사할 수 있다.
- Y 실제 선형회귀식 , Y' : 최소제곱법으로 얻어진 이상적 선형회귀식 , SE : 평균 오차값 , x: 독립변수 , y : 종속변수
각주[편집]
- 내용주
- 참조주
- ↑ David A. Freedman (2009). 《Statistical Models: Theory and Practice》. Cambridge University Press. 26쪽.
A simple regression equation has on the right hand side an intercept and an explanatory variable with a slope coefficient. A multiple regression equation has several explanatory variables on the right hand side, each with its own slope coefficient
- ↑ Rencher, Alvin C.; Christensen, William F. (2012), 〈Chapter 10, Multivariate regression – Section 10.1, Introduction〉, 《Methods of Multivariate Analysis》, Wiley Series in Probability and Statistics 709 3판, John Wiley & Sons, 19쪽, ISBN 9781118391679
- ↑ Yan, Xin (2009), 《Linear Regression Analysis: Theory and Computing》, World Scientific, 1–2쪽, ISBN 9789812834119,
Regression analysis ... is probably one of the oldest topics in mathematical statistics dating back to about two hundred years ago. The earliest form of the linear regression was the least squares method, which was published by Legendre in 1805, and by Gauss in 1809 ... Legendre and Gauss both applied the method to the problem of determining, from astronomical observations, the orbits of bodies about the sun.
- ↑ Tofallis, C (2009). “Least Squares Percentage Regression”. 《Journal of Modern Applied Statistical Methods》 7: 526–534. doi:10.2139/ssrn.1406472.
- ↑ del Pino, Guido (1989). “The Unifying Role of Iterative Generalized Least Squares in Statistical Algorithms”. 《Statistical Science》 4 (4): 394–403. doi:10.1214/ss/1177012408. JSTOR 2245853.
- ↑ Carroll, Raymond J. (1982). “Adapting for Heteroscedasticity in Linear Models”. 《The Annals of Statistics》 10 (4): 1224–1233. doi:10.1214/aos/1176345987. JSTOR 2240725.
- ↑ Cohen, Michael; Dalal, Siddhartha R.; Tukey,John W. (1993). “Robust, Smoothly Heterogeneous Variance Regression”. 《Journal of the Royal Statistical Society, Series C》 42 (2): 339–353. JSTOR 2986237.
- ↑ Nievergelt, Yves (1994). “Total Least Squares: State-of-the-Art Regression in Numerical Analysis”. 《SIAM Review》 36 (2): 258–264. doi:10.1137/1036055. JSTOR 2132463.
- ↑ Narula, Subhash C.; Wellington, John F. (1982). “The Minimum Sum of Absolute Errors Regression: A State of the Art Survey”. 《International Statistical Review》 50 (3): 317–326. doi:10.2307/1402501. JSTOR 1402501.
- ↑ Stone, C. J. (1975). “Adaptive maximum likelihood estimators of a location parameter”. 《The Annals of Statistics》 3 (2): 267–284. doi:10.1214/aos/1176343056. JSTOR 2958945.
- ↑ Deaton, Angus (1992). 《Understanding Consumption》. Oxford University Press. ISBN 0-19-828824-7.
- ↑ Laidler, David E. W. (1993). “The Demand for Money: Theories, Evidence, and Problems” 4판. New York: Harper Collins. ISBN 0065010981.
- ↑ 가 나 Ehrenberg; Smith (2008). 《Modern Labor Economics》 10 international판. London: Addison-Wesley. ISBN 9780321538963.
- ↑ “EEMP webpage”. 2011년 6월 11일에 원본 문서에서 보존된 문서. 2010년 3월 3일에 확인함.
같이 보기[편집]
외부 링크[편집]
- “Linear regression”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
- Weisstein, Eric Wolfgang. “Linear regression”. 《Wolfram MathWorld》 (영어). Wolfram Research.




























![{\displaystyle \operatorname {E} [\,\mathbf {x} _{i}\varepsilon _{i}\,]=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4fe630b8dd4a94034014b5574c04f48c623761d9)







![{\displaystyle l(\theta )=\sum _{i=1}^{N}\log[({\frac {1}{2\pi \sigma ^{2}}})^{2}exp(-{\frac {1}{2\sigma ^{2}}}(y_{i}-{\boldsymbol {\beta }}^{T}\mathbf {x_{i}} )^{2})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7bc1eb44a2565cfffa2189d4712c263f14f3ce9)













