비오-사바르 법칙
 |
| 전기 · 자기 |
비오-사바르 법칙(Biot-Savart法則, Biot–Savart law)은 전자기학에서 주어진 전류가 생성하는 자기장이 전류에 수직이고 전류에서의 거리의 역제곱에 비례한다는 물리 법칙이다. 또한 자기장이 전류의 세기, 방향, 길이에 연관이 있음을 알려준다. 비오-사바르 법칙은 전자기학에서 유효하며 앙페르 회로 법칙과 가우스 자기 법칙과 일맥상통한다. 이 법칙의 이름은 이 법칙을 발견한 장바티스트 비오와 펠릭스 사바르(Félix Savart)의 이름을 땄다.
정의[편집]
원점 에 전류 가 무한소의 길이의 전선 을 따라 흐른다고 하자. 그렇다면 이 무한소의 전선에 흐르는 전류에 의하여 발생하는 무한소의 자기장 은 다음과 같다.
- .
여기서 은 의 방향의 단위벡터이고, 은 진공의 투자율이다.
유한한 길이의 전선을 따라 흐르는 전류의 경우, 양변을 적분하면 전류로 인하여 발생하는 총 자기장을 알 수 있다.
활용[편집]
직선 전류에 의한 자기장과 솔레노이드 내부의 자기장은 앙페르 법칙을 이용해 구할 수 있고, 비오-사바르 법칙은 원형 전류 중심에서의 자기장의 세기를 구하는 데 이용된다.
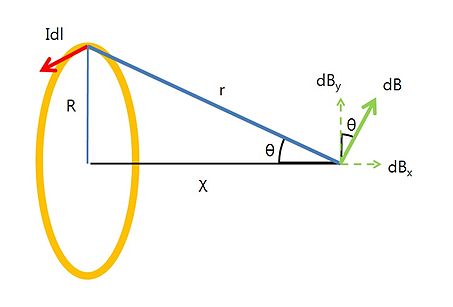
원형 도선이 있을 때, 전류 요소 Idl은 지면 앞으로 나오는 방향이고, r에 수직이다. 또 dB의 방향도 r에 수직인 방향이 된다.
r2=x2+R2이므로 비오-사바르 법칙에서 다음과 같다.
원형 전류의 각 전류 요소 Idl에 의한 자기장 dB를 그 회로에 따라 모두 합하면 회로축에 수직인 dB의 y성분은 상쇄되므로 dB의 x성분만 계산하면 된다.
같이 보기[편집]
외부 링크[편집]
- Science World - Biot-Savart Law
- Fu-Kwun Hwang (2001년 2월 22일). “비오-사바르 법칙의 증명 방법”. 2012년 8월 20일에 확인함.