정팔면체
보이기
(엇삼각기둥에서 넘어옴)
| 정팔면체 | |
|---|---|
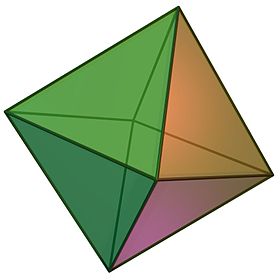 (클릭해서 회전하는 모델을 볼 수 있다) | |
| 종류 | 플라톤 다면체 |
| 성분 | F = 8, E = 12 V = 6 (χ = 2) |
| 면의 수{변의 수} | 8{3} |
| 콘웨이 표기 | O aT |
| 슐레플리 기호 | {3,4} |
| r{3,3} or | |
| 면 배치 | V4.4.4 |
| 위토프 기호 | 4 | 2 3 |
| 콕서터 다이어그램 | |
| 대칭 | Oh, BC3, [4,3], (*432) |
| 회전군 | O, [4,3]+, (432) |
| 참조 | U05, C17, W2 |
| 특성 | 정다면체, 볼록델타다면체 |
| 이면각 | 109.47122° = arccos(−13) |
 3.3.3.3 (꼭짓점 도형) |
 육면체 (쌍대 다면체) |
 전개도 | |
정팔면체(正八面體, octahedron)는 한 개의 꼭짓점에 네 개의 면이 만나고, 여덟 개의 정삼각형 면으로 이루어진 3차원 정다면체이다. 면의 수는 8개, 꼭짓점의 수는 6개로 정육면체와 서로 반대이다. 모서리의 개수는 12개이다. 그러므로 정팔면체는 정육면체와 서로 쌍대다면체이다. 참고로 정팔면체는 사각쌍뿔로 생각하거나 보아도 되며 꼭짓점이 사각뿔인데, 엇정삼각기둥으로 볼 수 있다. 또한 정사면체의 각 꼭짓점을 모서리의 절반 지점까지 깎아서도 만들 수 있다고 하여 사사면체 라고 한다. 이면각은 109.47°이며, 이는 정사면체와 함께 조합한다면 3차원 공간을 가득 채울 수 있는데, 이것의 쌍대는 마름모십이면체 벌집이다. 한 모서리에 모일 수 있는 정팔면체의 개수는 3개이다. 이는 각각 정이십사포체에 해당한다.
구와 정팔면체의 관계
[편집]정팔면체의 모서리 길이가 a이면, 외접구(모든 꼭짓점에서 팔면체와 접촉하는 구)의 반지름은 다음과 같다.
팔면체의 각 면에 내접하는 내접구의 반지름은 다음과 같다.
각각의 모서리의 중앙을 지나는 구의 반지름은 다음과 같다.
겉넓이와 부피
[편집]한 모서리의 길이가 인 정팔면체의 부피와 겉넓이는 다음과 같다.
또한, 한 모서리의 길이가 인 정육면체에 꼭 맞게 들어가는 정팔면체의 부피는 다음과 같다.
비슷한 다면체
[편집] 정육면체 |
 깎은 정육면체 |
 육팔면체 |
 깎은 정팔면체 |
| 이 글은 기하학에 관한 토막글입니다. 여러분의 지식으로 알차게 문서를 완성해 갑시다. |








