파란 선이 쌍곡선 궤도를 나타낸다. 그림에서 "우물"의 깊이는 위치 에너지 를 나타내고, 궤도의 운동 에너지 는 빨간색으로 표시되어 있다. 쌍곡선 궤도는 그림의 오른쪽 아래에 표시되어 있다. 천체물리학 및 궤도역학 에서 쌍곡선 궤도 (영어 : hyperbolic orbit ) 또는 쌍곡선 궤적 (영어 : hyperbolic trajectory )[참조 1] 탈출 속도 보다 더 빠른 속도로 궤도 중심체 를 탈출하는 물체의 궤도이다. 수학적으로는 궤도 이심률 이 1보다 큰 궤도로 정의된다. 이름은 아이작 뉴턴 의 만유인력의 법칙 에서 유도된 것으로, 위와 같은 궤도의 모양은 쌍곡선 이 된다는 것에서 유래하였다.
일반적으로, 중심체의 탈출 속도 를 넘어 쌍곡선 궤도를 따르는 물체는 영원히 움직이리라 여겨지며, 쌍곡선 궤도는 포물선 궤도 처럼 탈출 궤도 이다. 쌍곡선 궤도의 고유 궤도 에너지 의 값은 양수이다.
우주 탐사선의 스윙바이 또한 쌍곡선 궤도로 설명할 수 있다.
쌍곡선 궤도를 설명하는 변수 [ 편집 ] 타원 궤도처럼, 쌍곡선 궤도는 (앞의 정의를 무시하고) 궤도의 장축단과 이심률로 정의될 수 있다. 하지만 쌍곡선 궤도에서는 다른 변수들이 물체의 운동을 서술하기 더 적합한 경우도 있다. 다음 표는 쌍곡선 궤도를 따르는 물체를 서술하는 주요 변수들을 공식과 함께 나타낸 것이다.
쌍곡선 궤도 변수
변수
기호
공식
v
∞
{\displaystyle v_{\infty }}
a
{\displaystyle a}
b
{\displaystyle b}
표준 중력 변수
μ
{\displaystyle \mu \,}
v
2
(
2
/
r
−
1
/
a
)
{\displaystyle {\frac {v^{2}}{(2/r-1/a)}}}
b
v
∞
2
cot
θ
∞
{\displaystyle bv_{\infty }^{2}\cot \theta _{\infty }}
이심률 (>1)
e
{\displaystyle e}
ℓ
r
p
−
1
{\displaystyle {\frac {\ell }{r_{p}}}-1}
1
+
b
2
/
a
2
{\displaystyle {\sqrt {1+b^{2}/a^{2}}}}
긴반지름 (<0)
a
{\displaystyle a\,\!}
1
/
(
2
/
r
−
v
2
/
μ
)
{\displaystyle 1/(2/r-v^{2}/\mu )}
−
μ
/
v
∞
2
{\displaystyle -\mu /v_{\infty }^{2}}
쌍곡선 초과 속도
v
∞
{\displaystyle v_{\infty }}
−
μ
/
a
{\displaystyle {\sqrt {-\mu /a}}}
점근선 간의 (외부) 각도
2
θ
∞
{\displaystyle 2\theta _{\infty }}
2
cos
−
1
(
−
1
/
e
)
{\displaystyle 2\cos ^{-1}(-1/e)}
π
+
2
tan
−
1
(
b
/
a
)
{\displaystyle \pi +2\tan ^{-1}(b/a)}
충돌 변수 (장반경 )
b
{\displaystyle b}
−
a
e
2
−
1
{\displaystyle -a{\sqrt {e^{2}-1}}}
{\displaystyle }
반통경[참조 2]
ℓ
{\displaystyle \ell }
a
(
e
2
−
1
)
{\displaystyle a(e^{2}-1)}
b
2
/
a
=
h
2
/
μ
{\displaystyle b^{2}/a=h^{2}/\mu }
근지점 거리
r
p
{\displaystyle r_{p}}
a
(
e
−
1
)
{\displaystyle a(e-1)}
a
2
+
b
2
+
a
{\displaystyle {\sqrt {a^{2}+b^{2}}}+a}
고유 궤도 에너지
ε
{\displaystyle \varepsilon }
−
μ
/
2
a
{\displaystyle -\mu /2a}
v
∞
2
/
2
{\displaystyle v_{\infty }^{2}/2}
특정 각운동량
h
{\displaystyle h}
μ
ℓ
{\displaystyle {\sqrt {\mu \ell }}}
b
v
∞
{\displaystyle bv_{\infty }}
긴반지름, 에너지 및 쌍곡선 탈출 속도 [ 편집 ] 궤도 긴반지름(
a
{\displaystyle a\,\!}
점근선 이 만나는 곳까지의 거리로 정의될 수 있다. 일반적으로 이 값은 음수인데, 이는 다양한 타원 궤도 방정식에 대하여 일관성을 유지하기 위한 것이다.
궤도 긴반지름은 고유 궤도 에너지 (
ϵ
{\displaystyle \epsilon \,}
특성 에너지 (
C
3
{\displaystyle C_{3}}
v
∞
{\displaystyle v_{\infty }\,\!}
v
∞
2
=
2
ϵ
=
C
3
=
−
μ
/
a
{\displaystyle v_{\infty }^{2}=2\epsilon =C_{3}=-\mu /a}
a
=
−
μ
/
v
∞
2
{\displaystyle a=-{\mu /{v_{\infty }^{2}}}}
여기서
μ
{\displaystyle \mu }
표준 중력 변수 이다.
참고로, 쌍곡선 궤도에서의 총 에너지량은 양수이다(타원 궤도의 경우에는 음수이다).
이심률과 접근 및 탈출 때의 각도 [ 편집 ] 쌍곡선 궤도에서 궤도 이심률
e
{\displaystyle e\,}
점근선 간 각도에 직접적으로 연관되어 있다. 이심률이 1보다 약간 클 때는 궤도가 각진 "V" 모양이다.
e
=
2
{\displaystyle e={\sqrt {2}}}
e
>
2
{\displaystyle e>2}
궤도 중심체의 점근선과 근점 방향 사이의 각도는 거리가 무한대가 될 때의 진근점 이각 (
θ
∞
{\displaystyle \theta _{\infty }\,}
2
θ
∞
{\displaystyle 2\theta _{\infty }\,}
θ
∞
=
cos
−
1
(
−
1
/
e
)
{\displaystyle \theta {_{\infty }}=\cos ^{-1}(-1/e)\,}
e
=
−
1
/
cos
θ
∞
{\displaystyle e=-1/\cos \theta {_{\infty }}\,}
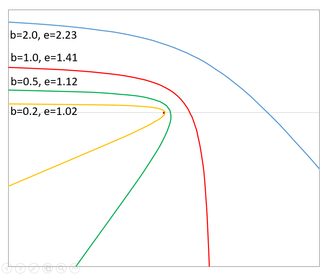
각각 쌍곡선 초과 속도와 궤도 긴반지름이 같고 같은 방향에서 오지만, 충돌 변수와 궤도 이심률이 다른 물체들의 궤도를 나타낸 그림. 운동에 관한 방정식 [ 편집 ] 쌍곡선 궤도에서는 진근점 이각 (
θ
{\displaystyle \theta }
물체 사이의 거리(
r
{\displaystyle r\,}
r
=
ℓ
1
+
e
⋅
cos
θ
{\displaystyle r={\frac {\ell }{1+e\cdot \cos \theta }}}
진근점 이각 θ 와 편심 이각 E 사이의 관계는 다음과 같다.
cosh
E
=
cos
θ
−
e
1
−
e
⋅
cos
θ
{\displaystyle \cosh {E}={{\cos {\theta }-e} \over {1-e\cdot \cos {\theta }}}}
tan
θ
2
=
1
+
e
1
−
e
⋅
tanh
E
2
{\displaystyle \tan {\frac {\theta }{2}}={\sqrt {\frac {1+e}{1-e}}}\cdot \tanh {\frac {E}{2}}}
편심 이각 E 는 케플러 방정식에 따라 평균 근점 이각 M 과 다음과 같은 관계가 있다.
M
=
e
sinh
E
−
E
{\displaystyle M=e\sinh E-E}
또한 평균 근점 이각은 시간과 비례한다.
M
=
μ
−
a
3
.
(
t
−
τ
)
{\displaystyle M={\sqrt {\frac {\mu }{-a^{3}}}}.(t-\tau )}
여기서 μ 는 표준 중력 변수 이고, a 는 궤도 긴반지름 이다.
비행 경로각 [ 편집 ] 비행 경로각 φ 는 속도의 방향과 반경 방향에 수직한 방향 사이의 각도로, 근점에서는 0이 되고 90도는 무한대를 가리킨다.
tan
(
ϕ
)
=
e
⋅
sin
θ
1
+
e
⋅
cos
θ
{\displaystyle \tan(\phi )={\frac {e\cdot \sin \theta }{1+e\cdot \cos \theta }}}
쌍곡선 궤도에서의 궤도 속도
v
{\displaystyle v\,}
활력방정식 을 통해서 계산될 수 있다.
v
=
μ
(
2
r
−
1
a
)
{\displaystyle v={\sqrt {\mu \left({2 \over {r}}-{1 \over {a}}\right)}}}
μ
{\displaystyle \mu \,}
표준 중력 변수 이다.
r
{\displaystyle r\,}
a
{\displaystyle a\,\!}
긴반지름 으로, 음수이다.일반적인 추정에 따라, 궤도의 어느 지점에서나 궤도 속도(
v
{\displaystyle v\,}
탈출 속도 (
v
e
s
c
{\displaystyle {v_{esc}}\,}
v
∞
{\displaystyle v_{\infty }\,\!}
v
2
=
v
e
s
c
2
+
v
∞
2
{\displaystyle v^{2}={v_{esc}}^{2}+{v_{\infty }}^{2}}
상대론에서의 이체 문제 [ 편집 ] 일반 상대성이론 의 이체 문제 에서는, 탈출에 충분한 에너지를 가져 탈출하는 물체들의 궤도는 더 이상 쌍곡선 모양이 아니다. 하지만, 탈출하는 물체들의 궤적은 여전히 "쌍곡선 궤도"라고 불린다.
같이 보기 [ 편집 ] 내용주
↑ 궤도 의 정의(다른 물체 주위를 도는 현상)에 따라, 엄밀히는 쌍곡선 궤적이 올바른 표현이나, 이 문서에서는 통용되는 표기를 따랐다.↑ 타원의 초점에서 주축(major axis)에 수직이 되게 곡선까지 잰 거리
참조주
Vallado, David A. (2007). 《Fundamentals of Astrodynamics and Applications, Third Edition》. Hawthorne, CA.: Hawthorne Press. ISBN 978-1-881883-14-2
외부 링크 [ 편집 ]