적색편이
| 시리즈의 일부 |
| 물리 우주론 |
|---|
|
대폭발(빅뱅) · 우주 우주의 나이 우주의 역사 |
|
|

적색편이(赤色偏移, 영어: redshift 레드시프트[*])는 물체가 내는 빛의 파장이 늘어나 보이는 현상이다. 일반적으로 전자기파의 가시광선 영역에서, 파장이 길수록 (진동수가 작을수록) 붉게 보이기 때문에, 물체의 스펙트럼이 붉은색 쪽으로 치우친다 의미에서 적색(赤色) 편이(偏移)라고 불린다.
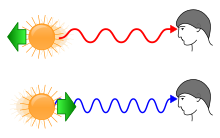
적색편이는 여러 원인에 의해 일어나는데, 가장 대표적인 것은 도플러 효과(Doppler effect)에 의한 것이다. 예를 들어, 사이렌을 울리는 소방차가 관측자에게 다가올 때는, 사이렌의 음높이가 높게 들리지만, 옆을 지나쳐서 멀어져 갈 때는 반대로 소리가 낮게 들리는 것을 느낄 수 있다. 이처럼 빛을 내는 천체가 관측자로부터 멀어지는 경우, 빛의 파장이 길어지게 된다. 우주론적 적색편이(cosmological redshift)는 공간의 팽창 자체 때문에 빛의 파장이 길어지는 현상으로 지구에서 수 백만 - 수십억 광년 만큼 아주 멀리 떨어져 있는 천체들로부터 관측된다. 마지막으로 중력 적색편이 현상(gravitational redshift)은 일반 상대론적 효과로서, 빛이 강한 중력장에서 빠져나오면서 에너지를 잃기 때문에 파장이 길어지는 현상이다. 적색편이의 반대말로 빛의 파장이 줄어들어 보이는 현상은 청색편이(blueshift)라고 하며, 빛을 내는 물체가 관측자에 가까워지거나, 빛이 중력장 안으로 들어갈 때 발생한다.
우리 주위에서 적색 또는 청색편이 현상을 실생활에 응용하는 예로서는 기상관측용 도플러 레이다나 경찰이 속도위반을 단속하는데 쓰는 스피드 건(Radar gun)등이 있지만, 가장 대표적인 적색편이 현상은 주로 천문학에서 천체들의 스펙트럼에서 관측된다.[1][2][3]
민코프스키 공간에서는 특수상대론의 공식을 이용하면, 관측자 부근에서 움직이고 있는 물체의 적색편이를 계산할 수 있다. 반면 블랙홀 주변처럼 중력이 강한 곳이나 전 우주적 규모에서의 적색편이를 이해하기 위해서는 일반 상대성 이론을 이용해야 한다.[4] 일반적으로 이러한 특수 상대성 이론, 중력적, 또는 우주론적 적색편이 현상은 좌표계의 변환(frame transformation laws)이라는 관점에서 설명된다. 한편 이러한 관측자, 광원의 좌표계 사이의 변환 때문에 생기는 적색편이 외에도, 빛의 산란이나 광학적 효과에 의해 빛의 파장이 변하는 경우도 있는데, 이러한 경우에는 적색 또는 청색편이라는 용어보다는 빛의 복사전달의 관점에서 주로 서술된다.
역사[편집]
적색편이의 역사는 19세기 파동역학의 발전과 도플러 효과에 대한 연구로 거슬러 올라간다. 도플러 효과는 1842년에 이 원리를 처음으로 제시한 오스트리아의 과학자 크리스티안 도플러의 이름을 딴 것이다.[5] 도플러는 파동을 내는 물체가 관측자에 대해 움직일 경우, 관측되는 파동의 파장이나 주파수가 달라질 수 있다고 제안했는데, 이 가설은 1845년에 네덜란드의 과학자 Christophorus Buys Ballot이 음파를 이용하여 처음으로 확인하였다.[6] 한편 도플러는 이중성의 색깔이 별들의 운동속도 때문에 달리 보인다는 가설을 제시했지만, 실제로 별들의 색깔이 다른 이유는 별의 온도가 다르기 때문이며, 별의 속도는 별빛의 색깔을 바꿀 만큼 크지는 않다. 비록 그의 이중성에 대한 가설은 옳지 않음이 밝혀졌지만, 도플러가 제시한 원리는 현재 천문학에서 천체들의 속도를 측정하는데 널리 사용되고 있다.[7]
천문학에서의 도플러 효과에 의한 적색편이는 1848년에 피조(Hippolyte Fizeau)에 의해 처음으로 관측되었다. 그는 별빛의 선스펙트럼의 파장이 변하는 것을 발견했는데, 이 효과는 "도플러-피조 효과"라고 불리기도 한다. 1868년에는 영국의 천문학자 윌리엄 허긴스가 처음으로 지구로부터 멀어지지는 별의 속도를 측정했다.[8] 1871년에는 태양의 자전 때문에 프라운호퍼 선들이 약 0.1Å 정도 편이되는 현상이 관측되었다.[9] 1887년에는 보겔(독일어: Vogel)과 샤이너(독일어: Scheiner)가 지구의 공전 때문에 별빛의 파장이 1년에 걸쳐 주기적으로 변하는 현상을 발견했다.[10] 1901년에는 Aristarkh Belopolsky가 실험실에서 회전하는 거울을 이용하여 도플러-피조 효과를 재현해냈다.[11]
적색-편이("red-shift")란 용어가 이음표가 있는 상태로 처음 쓰이게 된 것은 미국의 천문학자 월터 아담스(Walter S. Adams)가 1908년에 "성운의 적색-편이(red-shift)의 본질을 연구하는 방법"이라고 쓰면서부터이다.[12] 붙여쓴 적색편이("redshift")는 1934년에 드 시터(Willem de Sitter)에 의해 쓰이기 시작했으며, 그 전에는 독일어인 Rotverschiebung이 널리 쓰였던 것으로 보인다.[13]
베스토 슬라이퍼는 1912년에 당시에는 '나선 성운'이라고 불리던 은하들이 상당히 큰 적색편이 값을 보인다는 것을 발견했다.[14][15] 슬라이퍼는 이 논문에서 온 하늘에 고루 분포하는 나선은하들의 속도를 측정했는데, 그 중 3개를 제외하고는 모든 은하가 우리 은하로부터 약 수백 또는 천 km/s의 속도로 멀어지고 있는 것을 발견했다. 이 후에 에드윈 허블은 은하들의 적색편이(속도)와 은하들까지의 거리가 비례한다는 허블의 법칙을 발견하였다.[16] 이러한 발견들은 1922년에 알렉산드르 프리드만이 일반 상대성 이론으로부터 이론적으로 유도한 것처럼 우주가 정적이지 않고 팽창하고 있다는 것을 관측으로 뒷받침하는 것이었다.[17] 현재 이 발견들은 우주의 팽창과 대폭발 이론을 뒷받침하는 가장 중요한 근거로 받아 들여지고 있다.[18]
적색편이의 측정과 해석[편집]

어떤 물체의 적색편이는 그 물체가 내는 빛의 스펙트럼을 얻은 후, 그 스펙트럼에서 이미 알려져 있는 특징들을 그 물체가 정지해 있을 때의 스펙트럼과 비교함으로써 측정할 수 있다. 만약 이 스펙트럼이 방출선 또는 흡수선을 포함하고 있다면, 관측된 선 스펙트럼의 파장과 실험실에서 측정한 움직이지 않는 광원이 내는 파장을 비교함으로써 아래의 표와 같이 적색편이 값을 결정할 수 있다. 예를 들어, 오른쪽 위의 그림에서처럼, 멀리 떨어져 있는 은하의 스펙트럼에서 흡수선(그림에서는 가로로 된 검은띠로 보인다)이 관측되었다고 하자. 이 스펙트럼을 정지해 있는 물체(여기서는 태양)가 내는 스펙트럼과 나란히 비교하면 화살표가 보여주듯이 같은 패턴을 가진 흡수선들 전체가 파장이 긴 쪽으로, 다시 말해 붉은색 쪽으로, 이동해 있음을 볼 수 있다. 이러한 흡수선들은 별들이 내는 빛이 어떤 특정한 원소들로 이루어진 가스[주 1]를 통과하면서 그 원소들이 특정 파장의 빛만 선택적으로 흡수하기 때문에 발생한 것이다. 이러한 흡수선들의 패턴이 발견되면, 실험실에서 측정해 두었던 원소의 파장과 비교하여 파장이 길어진 정도를 다음과 같이 계산한다.
적색편이는 광원에서 낸 빛의 파장(또는 주파수)과 관측자가 보는 빛의 파장의 차이를 이용하여 결정할 수 있다. 천문학에서는 다음과 같이 차원이 없는 라는 값으로 적색편이를 표현한다. 예를 들어 와 가 각각 파장과 주파수를 나타낸다고 하고, 첨자인 'obsv'와 'emit'이 관측자(observer)와 광원(emitter)에서 각각 측정된 값을 의미한다고 하면, 아래의 표와 같이 적색편이값()이 정의된다.
| 파장을 이용한 계산 | 주파수를 이용한 계산 |
|---|---|
도플러 적색편이의 경우 가 측정되면, 그 부호로써 적색편이인지 청색편이인지 구분할 수 있다. 가 0보다 클 경우는 파장이 원래보다 길어졌으므로, 물체가 멀어지고 있는 적색편이에 해당한다. 반대로 가 음수일 경우에는 물체가 관측자에게 가까워지는 청색편이에 해당한다. 중력적 적색편이의 경우, 가 양수 일 경우는 빛이 관측자가 위치한 곳 보다 강한 중력장에서 빠져나온 경우를 의미한다. 한편, 우주의 팽창때문에 생기는 우주론적 적색편이의 경우에는 아주 가까이 있는 극소수의 은하들을 제외하고는 거의 모든 은하들에서 파장이 길어지는 적색편이() 현상이 관측된다.
적색편이 공식[편집]
일반상대론을 이용하면, 아래의 표와 같이 여러 가지 특수한 경우의 시공간에 대해 적색편이 공식을 유도할 수 있다. 모든 식에서 적색편이 값()은 측정에 사용된 빛의 파장과는 무관하다.
| 적색편이 종류 | 시공간 | 공식[주 2] |
|---|---|---|
| 상대론적 도플러 효과 | 민코프스키 공간(Minkowski space) (평탄한 시공간) |
(가 매우 작은 경우) (광원이 관측자로부터 시선방향으로 움직일 때) |
| 우주론적 적색편이 | FLRW 공간 (팽창하는 우주) | |
| 중력 적색편이 | 일반적인 정적인 시공간 (예를 들면, 슈바르츠실트 시공간) |
(슈바르츠실트 시공간) |
도플러 효과에 의한 적색편이[편집]
만약 광원이 관측자로부터 멀어질 경우, 적색편이가 일어나고(z > 0), 반대로 가까워질 경우에는 청색편이가 일어난다(z < 0). 이렇게 광원과 관측자의 상대적인 움직임 때문에 생기는 적색편이를 도플러 적색편이라고 부른다. 광원이 관측자에 대해 시선방향으로 광속(c)보다 매우 작은 속도 v로 움직이고 있다면, 적색편이는 다음과 같이 결정된다.
- ( 이면 이므로)
광원과 관측자 사이의 속도가 빛의 속도에 가까워지게 되면, 특수상대론을 이용하여 적색편이를 구해야 한다.[주 3] 광원이 빛에 가까운 속도로 움직일 경우에는, 특수상대론의 시간지연현상(time dilation) 때문에, 다음과 같이 로런츠 인자(Lorentz factor)라고 불리는 항이 적색편이 공식에 추가된다. 상대론적 도플러 효과는 1938년에 Ives-Stilwell 실험에서 처음으로 측정되었다.[20]
지금까지는 광원이 관측자에 대해 시선방향으로 멀어지거나 가까워지는 경우를 다루었지만, 일반적인 경우의 상대론적 적색편이는 다음과 같이 주어진다. 만약 θ가 관측자와 광원의 상대적인 운동사이의 각도라고 하면, 상대론적 적색편이는 다음과 같다.[21]
만약 광원이 시선방향으로만 움직이는 경우에는, 즉 θ = 0°인 경우, 위의 식은 다음과 같이 간단하게 줄어든다.
광원이 시선방향에 대해 수직으로 움직이는 특수한 경우를 (즉 θ = 90°)[22] 수직 도플러 효과(transverse redshift)라고 하며, 다음과 같이 적색편이가 주어진다:[23]
공간의 팽창에 의한 적색편이[편집]
20세기에 들어 먼 은하까지의 거리와 은하가 멀어지는 속도(적색편이)가 비례한다는 허블의 법칙이 발견되었다. 이 관측 결과와 일반상대론의 우주 모형 방정식을 이용하여, 우주는 중심이 없이 팽창하고 있다는 사실이 확립되었다. 허블이 관측한 먼 은하의 적색편이는 이러한 공간의 팽창 때문에 발생하는 우주론적 적색편이(cosmological redshift)이다. 현대 우주 표준 모형에서 먼 은하의 적색편이 값은 은하에서 빛이 방출되던 당시의 우주의 나이 그리고 당시 우주의 크기와 직접 연관되어 있다. 한때 적색편이를 설명하기 위해서 피곤한 빛 가설같은 설명이 제시되기도 했었지만, 현재는 받아 들여지지 않고 있다.[24]
우주론적 적색편이는 국지적인 도플러 효과 때문에 생기는 적색편이와 구분된다. 우주론적 적색편이는 관측자와 광원의 상대적인 움직임 때문에 생기는 것이 아니며, 빛(광자)이 전파되고 있는 공간 자체가 팽창하여 파장이 늘어나기 때문에 발생한다.[25] '공간'의 팽창 속도는 관측자와 광원의 거리가 멀수록 커지므로, 아주 멀리 떨어져 있는 은하는 빛의 속도보다 빠르게 멀어질 수도 있다. 이러한 사실은 마치 '모든 물체는 빛보다 빠르게 움직일 수 없다'는 특수상대론에 위배되는 것처럼 보일 수 도 있으나, 실제 은하는 자신이 속한 국지적인 좌표계에는 정지해 있으므로 실제로는 상대론에 위배되는 것이 아니다.
우주론적 적색편이의 수학적 유도[편집]
우주론적 적색편이를 유도하기 위해서는, 다음과 같이 팽창 우주에서 전파되고 있는 빛에 대하여 측지방정식(geodesic equation)을 적용해야 한다:[주 4]
여기서
- 은 시공간 간격(spacetime interval),
- 은 시간 간격(time interval),
- 은 공간 간격(spatial interval),
- 는 광속,
- 는 시간에 따라 변하는 우주의 척도인자(scale factor),
- 는 우주의 곡률을 나타낸다.
여기서 척도인자는 고유 거리(proper distance)와 공변 거리(comoving distance)의 비를 나타내는 값이다. 공변 거리는 같이 팽창하는 좌표계에서 어떤 기준 시점에서의 두 점 사이의 거리이고, 고유 거리는 실제 관측자가 측정하는 물리적인 거리이다. 두 점 사이의 거리가 , 공변 거리가 라면 이다. 따라서 척도인자는 두 시점 사이의 우주의 팽창 정도를 나타내는 값이다.
과거 어느 순간()에 먼 곳()에서 방출된 빛이, 현재 () 관측자가 위치한 곳()에 도달했다고 하자. 이 빛이 여행한 시공간의 경로에 대해 위의 측지방정식을 시간, 공간 항에 대해서 적분을 하면 다음과 같다:
이 빛이 방출될 때 광원(예를 들어 먼 은하)의 좌표계에서 이 빛의 파장을 , 빛이 현재의 관측자에게 도달했을 때의 파장을 이라고 하고, 이 두 파장 사이의 관계를 구하면 적색편이를 계산할 수 있다. 과거에 광원이 빛의 마루를 방출할 때의 파장이 이라면, 광원이 그 다음 마루를 방출한 시간은 다음과 쓸 수 있다.
한편, 현재의 관측자에게는 첫 번째 마루는 에 도착하게 되고, 그 다음의 두 번째 마루는 다음과 같이 만큼 나중에 도착하게 된다. 따라서 두 번째 마루가 도착한 시간은 관측자의 관점에서 볼 때는
- 이다.
이 두 번째 마루도 역시 를 출발해서 에 도착했으므로 같은 측지방정식을 적용하면:
위의 첫 번째 마루와 두 번째 마루에 대한 측지방정식의 오른쪽 항들이 같으므로
- ,
또는 적분을 정리하면
빛이 한 파장만큼 이동하는데 걸리는 시간 정도로 매우 작은 시간 간격 동안, 우주의 공간 척도인자()는 거의 변하지 않으므로, 적분 구간에 대해 상수로 근사할 수 있다. 따라서 위의 식은 다음과 같이 쉽게 적분할 수 있다.
위 식을 간단히 하면,
적색편이의 정의를 적용하고, 현재의 척도인자를 1이라고 정의하면 (, ), 다음과 같은 우주론적 적색편이 공식이 얻어진다.
요약하면, 먼 곳의 은하가 방출한 파장과 현재의 관측자에 도달한 빛의 파장의 비율은 당시의 우주와 현재 우주의 상대적 크기(척도 인자)의 비율이다. 이 척도 인자는 우주의 나이에 의해 결정되는 값이므로, 먼 은하의 적색편이는 당시 우주의 크기, 그리고 당시 우주의 나이에 의해 결정된다. 우리가 존재하는 팽창하는 우주에서 척도인자는 계속 증가하므로, 먼 우주에서 도달하는 빛의 적색편이는 항상 0보다 큰 값을 갖는다.
우주론적 적색편이와 국지적인 적색편이의 차이[편집]
일반적으로 먼 은하들의 적색편이는 우주의 팽창에 따른 우주론적 적색편이와 국지적인 특이운동(peculiar motion) 때문에 발생하는 도플러 적색편이 모두를 포함하고 있다.[26][27] 앞에서 잠시 언급된 것처럼, 공간의 팽창에 의한 적색편이와 국지적인 운동에 의한 도플러 적색편이 현상은 서로 구분된다. 이는 다음과 같이 풍선을 이용한 비유를 통해 쉽게 설명 할 수 있다. 풍선 위에 두 점이 그려져 있고, 이 두 점들에 물결 또는 파동 모양이 그려져 있다고 하자. 이 풍선에 바람을 넣으면 고무막이 늘어나며 두 점들 사이의 거리는 점점 증가하게 되고, 고무막에 그려져 있던 물결 모양의 크기도 같이 커지게 된다. 이 비유에서 풍선 고무막은 우주를 나타내고, 풍선 고무막이 늘어나는 것은 우주의 팽창을, 물결 모양이 커지는 것은 우주론적 적색편이를 나타낸다. 한편 두 점에 각각 개미가 살고 있다고 상상해 보자. 고무막이 서서히 늘어나도, 개미들은 스스로 움직이지 않고 있기 때문에 자신이 주위에 대해서는 정지해 있는 것처럼 느낄 것이다. 반면 고무막이 늘어나는 동안에 한 점에 있던 개미(B)가 어느 한 방향으로 움직인다고 가정해보자. 이 경우 정지해 있는 다른 개미(A)가 볼 때 B 개미는 고무막이 늘어나는 움직임에 더해서 추가로 움직이는 것처럼 보일 것이다. 이렇게 개미의 국지적인 움직임 때문에 추가로 적색편이 현상이 발생하게 되는데, 이것이 도플러 효과에 의한 적색편이이다.[28][29]
중력 적색편이[편집]
일반 상대론에 따르면, 중력장에서는 시간지연이 발생한다. 이 때문에 빛의 파장이 늘어나는 중력 적색편이가 발생하며, 이는 아인슈타인 편이라고도 불린다.[30] 전하가 없고, 회전하지 않는, 구면 대칭인 질량에 대한 일반상대론의 아인슈타인 방정식을 풀면 슈바르츠실트 해를 얻게 되는데, 이로부터 다음과 같은 중력적 적색편이 공식을 유도 할 수 있다.
여기서
- 는 중력상수,
- 는 중력장을 생성하는 물체의 질량,
- 은 슈바르츠실트 좌표계에서 물체까지의 거리,
- 는 빛의 속도를 나타낸다.
한편, 위의 중력적 적색편이 공식은 특수상대론과 등가원리(equivalence principle)를 이용해서도 유도할 수 있다.[31]
지구에 의해 만들어지는 중력 적색편이는 매우 작지만, 뫼스바우어 효과(Mössbauer effect)를 응용한 파운드-렙카(Pound-Rebka) 실험을 통해 처음으로 지상에서 측정되었다.[32] 한편 블랙홀 근처처럼 중력장이 매우 강한 곳에서는 이러한 적색편이 값은 매우 큰 값을 갖게 되며, 심지어 블랙홀의 사건 지평선(event horizon)에 가까워지면 그 적색편이 값은 무한대가 된다. 또한 우주 마이크로파 배경에서 관측되는 큰 규모의 온도 요동은 작스-울프 효과(영어: Sachs-Wolfe effect)라고 불리는 중력편이 현상 때문에 발생한다.[33][34]
천문학에서의 적색편이[편집]
천문학, 특히 천문 분광학에서 주로 관측되는 적색편이는 도플러 효과에 의한 적색편이와 우주론적 적색편이이다. 적색편이를 측정하기 위해서는 관측된 천체의 스펙트럼에서 흡수선이나 방출선과 같은 특징을 찾아내고, 이 선들이 실제로 관측된 파장과 실험실에서 얻어진 고유 파장을 비교함으로써 천체의 적색편이를 구하게 된다. 이러한 흡수선이나 방출선등은 그 천체에 존재하는 특정한 원소 때문에 생기는 것으로, 실험실에서 이러한 원소가 내는 빛의 파장을 결정할 수 있다.
일반적으로 천체의 적색편이는 스펙트럼을 측정하면 정확히 측정할 수 있지만, 천체의 스펙트럼을 얻는 일은 상당한 시간을 필요로 하므로 많은 천체들의 적색편이를 측정하는 것은 쉬운 일이 아니다. (적색편이 탐사를 참조.) 따라서 어떤 천체의 스펙트럼 자료가 없거나, 너무 어두워서 분광관측이 불가능할 경우, 천체의 측광자료를 이용하여 대략 적색편이 값을 추측할 수 있는데[35], 이렇게 얻어진 적색편이를 측광 적색편이(photometric redshift)라고 부른다. 반면 일반적인 적색편이는 분광 적색편이(spectroscopic redshift)라고 불린다.
가까운 우주에서의 적색편이[편집]
우리은하를 포함해 매우 가까운 은하들에서 관측되는 적색편이는 대부분 천체가 시선방향으로 움직이기 때문에 생기는 도플러 적색편이이다. 따라서 천문학자들은 적색편이(또는 청색편이)를 측정함으로써 천체의 속도를 측정하고, 천체의 물리적 특성들을 연구한다. 아래에 있는 여러 가지 예처럼, 적색편이 관측은 천문 분광학에서 가장 중요한 도구 중의 하나이다.
천문 분광학의 초기에 적색편이는 금성과 같은 태양계 행성들의 자전 속도를 측정하는데 이용되었다.[주 5] 이중성의 적색편이(즉 속도)를 측정하면 별들의 질량을 구할 수 있다. 때로는 하늘에서 볼 때 두 별이 매우 가까이 붙어 있어서, 사진에서는 짝별인지 홑별인지 구분하는게 불가능하고, 도플러 효과를 이용해야만 두 별로 이루어져 있음을 알 수도 있다. 이러한 쌍성을 분광쌍성이라고 부른다. 한편 이러한 도플러 효과 기술을 이용해 외계행성계(extrasolar planet)를 탐사하거나, 행성의 물리적 성질(공전주기, 행성 질량, 공전 궤도)을 연구하기도 한다. 또한 태양의 표면(광구)의 적색편이를 아주 정밀하게 측정하여 태양 표면의 미세한 진동을 연구하고 나아가 태양의 내부 구조를 연구하는 분야는 태양지진학(helioseismology)이라고 한다.[36]
우리은하 내부의 수소가스가 방출하는 21cm선의 적색편이와 폭을 측정하면, 우리 은하내의 성간물질이 어떻게 운동하는지 알아 낼 수 있다.[37] 한편 외부은하에서 적색편이가 은하 표면에 걸쳐 어떻게 변하는지를 측정하면,[주 6] 은하의 별, 가스들이 어떻게 회전하는지, 그리고 이를 이용하여 은하의 질량등을 알아낼 수 있다. 그리고 중성자별과 블랙홀에서 나오는 빛의 도플러, 중력적색편이로부터 이들 주변에서 물질이 어떻게 빨려들어가고 또 방출되기도 하는지 등을 연구할 수 있다.[38]
외부 은하의 적색편이[편집]
멀리 떨어져 있는 외부은하들로부터 관측되는 적색편이는 주로 우주 팽창에 의한 우주론적 적색편이이다. 멀리 떨어져 있는 은하일수록 큰 적색편이 값을 나타낸다는 허블의 법칙은 우주 팽창의 근거로 받아 들여지고 있다. 은하가 우리로부터 멀리 떨어져 있을수록, 빛이 은하에서 방출된 후에 우주가 더 많이 팽창했다는 뜻이며, 따라서 빛의 파장이 더 많이 늘어나게 되고, 빛이 더 큰 적색편이를 보이게 된다. 즉, 멀리 떨어져 있는 천체일수록 적색편이 값이 커지고 빛의 파장이 적색으로 치우치며 붉은색을 띤다. 현대 우주 모형에 따르면, 아주 멀리 있는 천체의 적색편이를 측정하면, 천체의 거리와 그 천체가 존재하는 과거 우주의 나이가 결정된다. 아주 멀리 있는 천체들의 거리를 직접 재는 것은 매우 힘들기 때문에, 수백 Mpc 이상 떨어져 있는 천체들의 경우, 그 적색편이를 측정하고, 표준 우주 모형을 적용하면 그 거리를 결정할 수 있다.
고적색편이 천체들[편집]
앞에서 설명한 것처럼, 어떤 천체가 멀리 떨어져 있을수록, 즉 우주가 더 젊었던 시기에 존재할수록, 더 큰 적색편이를 보인다. 따라서 천문학자들은 더욱 큰 적색편이를 갖는 천체들을 발견하기 위해 많은 노력을 기울이고 있다. 가장 큰 적색편이 값들은 주로 밝은 빛을 내는 퀘이사나 감마선 버스트 등에서 발견되고 있다.
현재 가장 신뢰할 수 있는 적색편이는 분광학 데이터에 의한 것으로, 가장 큰 적색편이는 GN-z11 은하에 의한 것인데,[39] z = 11.1의 적색편이를 보여주며 이는 대폭발 이후 4억년에 해당한다. 이보다 작은 적색편이는 UDFy-38135539[40]의 z = 8.6이고 이는 대폭발 이후 6억년에 해당한다. 또한 감마선폭발원(gamma ray burst)인 GRB 090423의 적색편이는 이다.[41] 가장 멀리 있는 퀘이사(quasar)는 ULAS J1120+0641로서 적색편이는 이다.[42][43] 퀘이사나 감마선폭발원이 아닌 천체 중 가장 멀리 떨어져 있는 천체는 IOK-1으로 에 위치해 있다.[44][주 7] 가장 멀리 있는 전파은하는 에 있는 TN J0924-2201이다.[45] 가장 멀리 있는 천체 중 일산화탄소 분자(CO)가 관측된 천체는 를 가진 SDSS J1148+5251 퀘이사이다.[46]
우주 마이크로파 배경의 적색편이는 이며 우주의 나이가 대폭발 이후 약 379,000년인 시기에 해당되고, 그 공변거리comoving distance)는 약 460억 광년이다. 이 우주 마이크로파 배경의 적색편이는 전자기파로 볼 수 있는 가장 먼 거리에 해당한다.[47] 아직 발견되지는 않았지만, "제 3 항성 종족"이라고 불리는 우주 최초의 별들은 약 에 있을 것으로 예측되고 있다.[48] 빅뱅 이후 약 2초후에 발생했을 것으로 예측되는 우주 중성미자 배경(cosmic neutrino background)은 그 적색편이가 에 해당한다.[49]
적색편이 탐사[편집]

큰 망원경의 등장과 천문 분광학(astronomical spectroscopy)의 발전 덕분에 근래에 들어 우주 거대구조의 지도를 만드는 '적색편이 탐사'(Redshift Survey)가 활발히 이루어지고 있다. 이러한 적색편이 탐사는 하늘의 일정 부분에 있는 많은 외부은하들의 스펙트럼을 얻고, 그 적색편이를 측정함으로써 은하들이 우주에서 어떻게 분포하는지를 보여주는 작업으로 우주의 지도를 만드는 것에 비견된다. 예를 들어 5억광년의 크기를 가진 만리장성(Great Wall)이라고 불리는 초은하단(supercluster)은 적색편이 탐사를 통해 발견된 최초의 우주 거대구조 중 하나이다.[50]
최초의 적색편이 탐사는 1977년에 시작되어 1982년에 끝난 CfA 적색편이 탐사(CfA Redshift Survey)이다.[51] 2002년에 완료된 2dF 적색편이 탐사는 약 220,000개의 은하들의 적색편이 값을 측정했다.[52] 역사상 가장 큰 규모의 적색편이 탐사는 슬론 디지털 전천 탐사(Sloan Digital Sky Survey, SDSS)로서 2013년 현재에도 진행 중이며 약 2백만개의 천체들의 적색편이를 측정했다.[53] 구경 2.5m의 망원경을 이용한 SDSS는 일반적인 은하들의 경우 약 적색편이가 0.3-0.4 정도까지 측정이 가능했고, 밝은 천체들의 경우 적색편이가 z = 6 이상인 퀘이사들도 발견했다. SDSS는 비교적 가까운 거리의 은하들의 지도를 넓은 영역에 걸쳐 작성한 반면, 켁 망원경을 이용한 DEEP2 적색편이 탐사는 z = 0.7 정도의 거리까지 은하들의 적색편이를 측정했다.[54]
복사 전달이나 광학 효과 때문에 생기는 현상[편집]
복사전달(radiative transfer)이나 물리 광학 분야에서 다루어지듯이, 빛이 물질과 상호 작용하고 전파되는 과정에서 빛의 파장 또는 주파수가 변할 수 있다. 이는 기준 좌표계의 변환 때문에 발생하는 적색편이와는 달리, 전파되는 빛(또는 광자)이 물질과 에너지를 주고 받으면서 파장의 변화가 일어난다. 예를 들면, 빛의 산란(scattering) 때문에 파장이 늘어나기도 하고, 전파되고 있는 매질의 굴절률의 바뀌기 때문에 파장이 변하기도 한다.[2] 이러한 현상들을 이를 때 종종 빛이 '적색편이'되었다거나 '청색편이'되었다는 용어를 사용하기도 하지만, 이는 여기서 설명된 적색편이와는 구분되어야 한다.
적색편이는 적색화 현상(reddening)과 혼동되어서는 안 된다. 적색화 현상(천문학에서는 성간적색화)은 파장이 짧은 빛이 파장이 긴 빛보다 쉽게 산란되기 때문에, 광원에서 방출된 여러 파장의 빛 중에서 주로 긴 파장의 빛이 관측자에게 주로 많이 도달하기 때문에 발생한다. 즉 적색편이처럼 광원에서 발생한 모든 스펙트럼 대역의 빛의 파장이 늘어나는 것이 아니라, 짧은 파장의 빛이 더 많이 흡수 또는 산란되어서 광원이 붉게 보이는 현상이다. 즉 광원의 전자기파 스펙트럼 모양이 바뀌는 현상이다. 이러한 적색화 현상의 대표적인 예로서는 해 질 녘 또는 해 뜰 무렵의 노을을 들 수 있다.
참고 문헌[편집]
- ↑ Feynman, Leighton and Sands (1989), Taylor (1992) 같은 물리학 입문서를 참조할 것.
- ↑ 가 나 Binney & Merrifeld (1998), Carroll & Ostlie (1996), Kutner (2003) 같은 일반 천문학 입문서를 참조할 것.
- ↑ 자일릭, 마이클 (2001년 9월 24일). 《천문학 및 천체물리학 서론(2판)》. 대한교과서. ISBN 978-89-378-0466-3. 2013년 6월 5일에 확인함.
- ↑ Misner, Thorne and Wheeler (1973), Weinberg (1971) 같은 우주론 책을 참고 할 것.
- ↑ Doppler, Christian (1846). “Beiträge zur fixsternenkunde”. 《Prag》 (Prag, Druck von G. Haase sohne) 69. Bibcode:1846QB815.D69......
- ↑ Maulik, Dev (2005). 〈Doppler Sonography: A Brief History〉. Maulik, Dev; Zalud, Ivica. 《Doppler Ultrasound in Obstetrics And Gynecology》. ISBN 978-3-540-23088-5.
- ↑ O'Connor, John J.; Roberston, Edmund F. (1998). “Christian Andreas Doppler”. 《MacTutor History of Mathematics archive》. University of St Andrews.
- ↑ Huggins, William (1868). “Further Observations on the Spectra of Some of the Stars and Nebulae, with an Attempt to Determine Therefrom Whether These Bodies are Moving towards or from the Earth, Also Observations on the Spectra of the Sun and of Comet II”. 《Philosophical Transactions of the Royal Society of London》 158: 529–564. Bibcode:1868RSPT..158..529H. doi:10.1098/rstl.1868.0022.
- ↑ Reber, G. (1995). “Intergalactic Plasma”. 《Astrophysics and Space Science》 227 (1–2): 93–96. Bibcode:1995Ap&SS.227...93R. doi:10.1007/BF00678069.
- ↑ Pannekoek, A (1961). 《A History of Astronomy》. Dover. 451쪽. ISBN 0-486-65994-1.
- ↑ Bélopolsky, A. (1901). “On an Apparatus for the Laboratory Demonstration of the Doppler-Fizeau Principle”. 《Astrophysical Journal》 13: 15. Bibcode:1901ApJ....13...15B. doi:10.1086/140786.
- ↑ Adams, Walter S. (1908). “Preliminary catalogue of lines affected in sun-spots”. 《Contributions from the Mount Wilson Observatory / Carnegie Institution of Washington》 (Contributions from the Solar Observatory of the Carnegie Institution of Washington: Carnegie Institution of Washington) 22: 1–21. Bibcode:1908CMWCI..22....1A. Reprinted in Adams, Walter S. (1908). “Preliminary Catalogue of Lines Affected in Sun-Spots Region λ 4000 TO λ 4500”. 《Astrophysical Journal》 27: 45. Bibcode:1908ApJ....27...45A. doi:10.1086/141524.
- ↑
de Sitter, W. (1934). “On distance, magnitude, and related quantities in an expanding universe”. 《Bulletin of the Astronomical Institutes of the Netherlands》 7: 205. Bibcode:1934BAN.....7..205D.
It thus becomes urgent to investigate the effect of the redshift and of the metric of the universe on the apparent magnitude and observed numbers of nebulae of given magnitude
- ↑
Slipher, Vesto (1912). “The radial velocity of the Andromeda Nebula”. 《Lowell Observatory Bulletin》 1: 2.56–2.57. Bibcode:1913LowOB...1b..56S.
The magnitude of this velocity, which is the greatest hitherto observed, raises the question whether the velocity-like displacement might not be due to some other cause, but I believe we have at present no other interpretation for it
- ↑ Slipher, Vesto (1915). “Spectrographic Observations of Nebulae”. 《Popular Astronomy》 23: 21–24. Bibcode:1915PA.....23...21S.
- ↑ Hubble, Edwin (1929). “A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae”. 《Proceedings of the National Academy of Sciences of the United States of America》 15 (3): 168–173. Bibcode:1929PNAS...15..168H. doi:10.1073/pnas.15.3.168. PMC 522427. PMID 16577160. 2008년 6월 30일에 원본 문서에서 보존된 문서. 2013년 10월 31일에 확인함.
- ↑ Friedman, A. A. (1922). “Über die Krümmung des Raumes”. 《Zeitschrift für Physik》 10 (1): 377–386. Bibcode:1922ZPhy...10..377F. doi:10.1007/BF01332580. English translation in Friedman, A. (1999). “On the Curve of Space”. 《General Relativity and Gravitation》 31 (12): 1991–2000. Bibcode:1999GReGr..31.1991F. doi:10.1023/A:1026751225741.)
- ↑ Eddington, Arthur (1933). 《The Expanding Universe: Astronomy's 'Great Debate', 1900–1931》. Cambridge University Press. (Reprint: ISBN 978-0-521-34976-5)
- ↑ “Hubble census finds galaxies at redshifts 9 to 12”. 《ESA/Hubble Press Release》. 2012년 12월 13일에 확인함.
- ↑ Ives, Herbert E.; G. R. Stilwell (1938). “An Experimental Study of the Rate of a Moving Atomic Clock”. 《Journal of the Optical Society of America》 28 (7): 215. doi:10.1364/JOSA.28.000215. ISSN 0030-3941.
- ↑ Freund, Jurgen (2008). 《Special Relativity for Beginners》. World Scientific. 120쪽. ISBN 981-277-160-3.
- ↑ Ditchburn, R (1961). 《Light》. Dover. 329쪽. ISBN 0-12-218101-8.
- ↑ "Photons, Relativity, Doppler shift Archived 2006년 8월 27일 - 웨이백 머신"를 참고.
- ↑ Goldhaber, G. (2001). “Timescale Stretch Parameterization of Type Ia SupernovaB‐Band Light Curves”. 《The Astrophysical Journal》 558 (1): 359–368. doi:10.1086/322460. ISSN 0004-637X.
- ↑ Harrison, Edward Robert (2000). 《Cosmology: The Science of the Universe》 2판. Cambridge University Press. 306ff쪽. ISBN 0-521-66148-X.
- ↑ Bedran,M.L.(2002) "A comparison between the Doppler and cosmological redshifts"; Am.J.Phys.70, 406–408 (2002)
- ↑ Edward Harrison (1992). “The redshift-distance and velocity-distance laws”. 《Astrophysical Journal》 403: 28–31. Bibcode:1993ApJ...403...28H. doi:10.1086/172179.
- ↑ Theo Koupelis, Karl F. Kuhn (2007). 《In Quest of the Universe》 5판. Jones & Bartlett Publishers. 557쪽. ISBN 0-7637-4387-9.
- ↑ Steven Weinberg (2008). 《Cosmology》. Oxford University Press. 11쪽. ISBN 978-0-19-852682-7.
- ↑ Chant, C. A. (1930). “Notes and Queries (Telescopes and Observatory Equipment – The Einstein Shift of Solar Lines)”. 《Journal of the Royal Astronomical Society of Canada》 24: 390. Bibcode:1930JRASC..24..390C.
- ↑ Einstein, A (1907). “Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen”. 《Jahrbuch der Radioaktivität und Elektronik》 4: 411–462.
- ↑ Pound, R.; Rebka, G. (1960). “Apparent Weight of Photons”. 《Physical Review Letters》 4 (7): 337. Bibcode:1960PhRvL...4..337P. doi:10.1103/PhysRevLett.4.337.
- ↑ Sachs, R. K.; Wolfe, A. M. (1967). “Perturbations of a cosmological model and angular variations of the cosmic microwave background”. 《Astrophysical Journal》 147 (73): 73. Bibcode:1967ApJ...147...73S. doi:10.1086/148982.
- ↑ “Dieter Brill, “Black Hole Horizons and How They Begin”, Astronomical Review (2012); Online Article, cited Sept.2012.”. 2014년 9월 16일에 원본 문서에서 보존된 문서. 2013년 10월 31일에 확인함.
- ↑ The technique was first described by Baum, W. A.: 1962, in G. C. McVittie (ed.), Problems of extra-galactic research, p. 390, IAU Symposium No. 15
- ↑ Libbrecht, Keng. (1988). “Solar and stellar seismology”. 《Space Science Reviews》 47 (3–4): 275–301. Bibcode:1988SSRv...47..275L. doi:10.1007/BF00243557.
- ↑ An early review by Oort, J. H. on the subject: Oort, J. H. (1970). “The formation of galaxies and the origin of the high-velocity hydrogen”. 《Astronomy and Astrophysics》 7: 381. Bibcode:1970A&A.....7..381O.
- ↑ Asaoka, Ikuko (1989). “X-ray spectra at infinity from a relativistic accretion disk around a Kerr black hole”. 《Astronomical Society of Japan》 41 (4): 763–778. Bibcode:1989PASJ...41..763A. ISSN 0004-6264.
- ↑ Oesch, P. A.; Brammer, G.; van Dokkum, P.; 외. (2016년 3월 1일). “A Remarkably Luminous Galaxy at z=11.1 Measured with Hubble Space Telescope Grism Spectroscopy”. 《The Astrophysical Journal》 819 (2): 129. arXiv:1603.00461. Bibcode:2016ApJ...819..129O. doi:10.3847/0004-637X/819/2/129. S2CID 119262750.
- ↑ M.D. Lehnert; Nesvadba, NP; Cuby, JG; Swinbank, AM; 외. (2010). “Spectroscopic Confirmation of a galaxy at redshift z = 8.6”. 《Nature》 467 (7318): 940–942. arXiv:1010.4312. Bibcode:2010Natur.467..940L. doi:10.1038/nature09462. PMID 20962840. S2CID 4414781.
- ↑ Salvaterra, R.; 외. (2009). “GRB 090423 reveals an exploding star at the epoch of re-ionization”. 《Nature》 461 (7268): 1258–60. arXiv:0906.1578. Bibcode:2009Natur.461.1258S. doi:10.1038/nature08445. PMID 19865166.
- ↑ http://www.universetoday.com/87175/most-distant-quasar-opens-window-into-early-universe/
- ↑ “Brilliant, but Distant: Most Far-Flung Known Quasar Offers Glimpse into Early Universe: Scientific American”.
- ↑ Masanori Iye; 외. (2006). “A galaxy at a redshift z = 6.96”. 《Nature》 443 (7108): 186–188. arXiv:astro-ph/0609393. Bibcode:2006Natur.443..186I. doi:10.1038/nature05104. PMID 16971942.
- ↑ Klamer, I. J.; Ekers, R. D.; Sadler, E. M.; Weiss, A.; Hunstead, R. W.; De Breuck, C. (2005). “CO (1-0) and CO (5-4) Observations of the Most Distant Known Radio Galaxy at z = 5.2”. 《The Astrophysical Journal》 621: L1. arXiv:astro-ph/0501447v1. Bibcode:2005ApJ...621L...1K. doi:10.1086/429147.
- ↑ Walter, Fabian; Bertoldi, Frank; Carilli, Chris; Cox, Pierre; Lo, K. Y.; Neri, Roberto; Fan, Xiaohui; Omont, Alain; Strauss, Michael A. (2003). “Molecular gas in the host galaxy of a quasar at redshift z = 6.42”. 《Nature》 424 (6947): 406–8. arXiv:astro-ph/0307410. Bibcode:2003Natur.424..406W. doi:10.1038/nature01821. PMID 12879063.
- ↑ Lineweaver, Charles; Tamara M. Davis (2005). “Misconceptions about the Big Bang”. Scientific American. 2008년 11월 6일에 확인함.
- ↑ Naoz, S.; Noter, S.; Barkana, R. (2006). “The first stars in the Universe”. 《Monthly Notices of the Royal Astronomical Society: Letters》 373: L98–L102. arXiv:astro-ph/0604050. Bibcode:2006MNRAS.373L..98N. doi:10.1111/j.1745-3933.2006.00251.x.
- ↑ Lesgourgues, J; Pastor, S (2006). “Massive neutrinos and cosmology”. 《Physics Reports》 429 (6): 307–379. arXiv:astro-ph/0603494. Bibcode:2006PhR...429..307L. doi:10.1016/j.physrep.2006.04.001.
- ↑ Geller, M. J.; Huchra, J. P. (1989). “Mapping the Universe”. 《Science》 246 (4932): 897–903. doi:10.1126/science.246.4932.897. ISSN 0036-8075.
- ↑ See the official CfA website for more details.
- ↑ Shaun Cole et al. (The 2dFGRS Collaboration) (2005). “The 2dF galaxy redshift survey: Power-spectrum analysis of the final dataset and cosmological implications”. 《Mon. Not. Roy. Astron. Soc.》 362 (2): 505–34. arXiv:astro-ph/0501174. Bibcode:2005MNRAS.362..505C. doi:10.1111/j.1365-2966.2005.09318.x. 2dF Galaxy Redshift Survey homepage Archived 2007년 2월 5일 - 웨이백 머신
- ↑ SDSS Homepage
- ↑ Marc Davis et al. (DEEP2 collaboration) (2002). 〈Science objectives and early results of the DEEP2 redshift survey〉. 《Conference on Astronomical Telescopes and Instrumentation, Waikoloa, Hawaii, 22–28 Aug 2002》. arXiv:astro-ph/0209419.
각주[편집]
- ↑ 천문학에서는 별의 대기라고 부른다.
- ↑ z = 적색편이; v|| = 시선방향과 평행한 속도 성분(관측자로부터 멀어지면 0보다 크다); c = 빛의 속도; γ = 로렌츠 인자(Lorentz factor; a = 척도인자(scale factor); G = 중력상수; M = 물체의 질량; r = 슈바르츠실트 좌표계에서 중심부터의 거리, gtt = metric tensor의 t,t 성분
- ↑ 자세한 설명은 도플러 효과#상대론적 도플러 효과(relativistic Doppler effect) 문서에 나와 있다.
- ↑ 이 방정식은 프리드만-르메트르-로버트슨-워커 계량(Friedmann–Lemaître–Robertson–Walker metric)으로부터 유도된다.
- ↑ 1871년에 Hermann Carl Vogel은 적색편이를 이용하여 금성의 자전속도를 추정했다.
- ↑ 천문학자들은 이를 은하의 속도곡선을 측정한다고 한다.
- ↑ 현재 UDFy-38135539라는 천체가 에 있다는 주장이 발표되었지만, 아직 다른 관측에 의해 확인되지는 않았다. 'Most distant galaxy ever found sheds light on Infant cosmos' 와 'VLT/XSHOOTER and Subaru/MOIRCS spectroscopy of HUDF.YD3: no evidence for Lyman α emission at z = 8.55'를 참고.
잡지 기사들[편집]
- Odenwald, S. & Fienberg, RT. 1993; "Galaxy Redshifts Reconsidered" in Sky & Telescope Feb. 2003; pp31–35
- Lineweaver, Charles H. and Tamara M. Davis, "Misconceptions about the Big Bang", Scientific American, March 2005.
기타 참고 서적[편집]
- Nussbaumer, Harry; and Lydia Bieri (2009). 《Discovering the Expanding Universe》. Cambridge University Press. ISBN 978-0-521-51484-2.
- Binney, James; and Michael Merrifeld (1998). 《Galactic Astronomy》. Princeton University Press. ISBN 0-691-02565-7.
- Carroll, Bradley W. and Dale A. Ostlie (1996). 《An Introduction to Modern Astrophysics》. Addison-Wesley Publishing Company, Inc. ISBN 0-201-54730-9.
- Feynman, Richard; Leighton, Robert; Sands, Matthew (1989). 《Feynman Lectures on Physics. Vol. 1》. Addison-Wesley. ISBN 0-201-51003-0.
- Grøn, Øyvind; Hervik, Sigbjørn (2007). 《Einstein's General Theory of Relativity》. New York: Springer. ISBN 978-0-387-69199-2.
- Kutner, Marc (2003). 《Astronomy: A Physical Perspective》. Cambridge University Press. ISBN 0-521-52927-1.
- Misner, Charles; Thorne, Kip S. and Wheeler, John Archibald (1973). 《Gravitation》. San Francisco: W. H. Freeman. ISBN 0-7167-0344-0.
- Peebles, P. J. E. (1993). 《Principles of Physical Cosmology》. Princeton University Press. ISBN 0-691-01933-9.
- Taylor, Edwin F.; Wheeler, John Archibald (1992). 《Spacetime Physics: Introduction to Special Relativity (2nd ed.)》. W.H. Freeman. ISBN 0-7167-2327-1.
- Weinberg, Steven (1971). 《Gravitation and Cosmology》. John Wiley. ISBN 0-471-92567-5.
외부 링크[편집]
- (영어) Ned Wright의 우주론 강의
- (영어) Mike Luciuk의 적색편이 강의
- (영어) 우주론적 효과를 나타낸 움직이는 그림 Wayne Hu의 홈페이지
- (영어) SIXTψ SYMBΦLS: 물리학과 천문학에서 쓰이는 기호들에 대한 영상들, "z 적색편이"




































































