우주의 나이
| 우주의 나이 | |
|---|---|
| 종류: | 천문 상수 |
| 값: | 1.3798 × 1010 년 |
| 오차: | ±0.0037 × 1010 년 |
| 출처: | Planck 2013년 데이터 (68% CL)[1]:Table 9 |
| 시리즈의 일부 |
| 물리 우주론 |
|---|
|
대폭발(빅뱅) · 우주 우주의 나이 우주의 역사 |
|
|
우주의 나이(영어: age of the universe)는 대폭발로부터 지금까지의 시간이다. 가장 최근(2013년 3월)의 관측과 ΛCDM 모형에 따르면 137.98 ± 0.37억 년이다.[1] 0.268%에 불과한 ±0.37억년의 정확도는 WMAP과 플랑크 인공위성의 우주 마이크로파 배경 관측으로부터 얻어졌다. 대폭발 이론에 따르면 우주는 초기의 매우 뜨거운 상태에서부터 점차 식어왔는데, 우주 마이크로파 배경의 현재 온도를 측정함으로써 대폭발 당시부터 현재까지 우주가 냉각되는데 걸리는 시간을 측정하는 원리이다.[2] 또한 현재의 우주의 팽창 속도를 측정하고, 이 값으로부터 거꾸로 우주의 크기가 0이 될 때까지의 시간을 계산하는 방법으로 우주의 나이를 추론할 수도 있다.
개요[편집]
ΛCDM 모형은 현재 천문학자들에게 널리 받아 들여지고 있는 이론으로써 우주가 매우 고온 고압의 원시 상태에서 시작해서 현재 상태에 이르기까지 137.98억년 동안의 진화를 설명하는 이론이다. 이 모형은 현재 이론적으로 매우 잘 이해되고 있으며, WMAP과 같은 매우 정밀한 관측 결과들에 의해 뒷받침되고 있다. 반면, 현대 물리학 및 천문학은 이 원시우주가 왜, 어떻게 시작되었는지는 잘 설명하지 못하는 한계를 가지고 있다. 만약 ΛCDM 모형을 우리가 잘 이해하고 있는 시기부터 계속 과거로 확장하면, 우주는 "대폭발 특이점"이라는 중력 특이점(特異點,singularity)에 도달하게 된다. 이 특이점에서는 물리학의 법칙이 적용되지 않기 때문에 이 점은 특별한 물리적 의미를 갖지는 못 한다. 하지만 편의 상 "우주의 나이"는 이 대폭발에서부터 현재까지 흐른 시간을 의미하는데 쓰이고 있다. 예를 들면, "대폭발 후 10−6초"는 우주의 진화에서 표준모형이 잘 적용되는 시간대이다. 따라서 "대폭발 후 10−6초"에서부터 현재까지의 시간은 매우 잘 정의되는 시간이지만, 이 때부터 대폭발 특이점까지의 시간은 잘 정의되지 않는다.
국제 천문 연맹[3] 은 "우주의 나이"를 ΛCDM 모형에서의 우주팽창이 지속된 시간, 또는 현재 관측 가능한 우주에서 대폭발부터 현재까지의 시간을 의미한다고 정하였다.
우주 나이의 하한선[편집]
아들이 아버지보다 나이가 많을 수 없는 것처럼, 우주 안의 천체는 당연히 우주보다는 젊어야 하기 때문에, 여러 종류의 천체를 관측하여 그 나이를 추정하는 것으로 우주의 나이의 하한선을 얻을 수 있다. 가장 많이 쓰이는 방법 중 하나는 가장 온도가 낮은 백색왜성의 나이를 측정하는 것이다. 백색왜성은 태양과 비슷한 질량을 가진 별들이 죽으면서 만들어지는데, 백색왜성은 당시 가지고 있던 열 이외에 다른 에너지원이 없기 때문에 나이가 들면서 점점 식고, 어두워지게 된다. 따라서 가장 어둡고, 가장 온도가 낮은 백색왜성을 찾아서 그 냉각 나이를 측정하면 우주의 나이의 하한선을 얻을 수 있다.
또 다른 방법은 가장 오래된 구상성단의 나이를 측정하는 방법이다. 처음에 성단이 만들어질 때 성단을 구성하는 별들은 모두 헤르츠스프룽-러셀 도표 위에서 주계열에 놓이게 된다. 그러나 성단이 나이를 먹어 가면서 가장 질량이 무거운 별들은 이 주계열에서부터 진화하기 시작하여 적색거성이 된다. 따라서 주계열에서 갈라지는 분기점을 통해 성단의 나이를 추정하여 우주의 나이의 하한선을 얻을 수 있다.
우주 변수[편집]
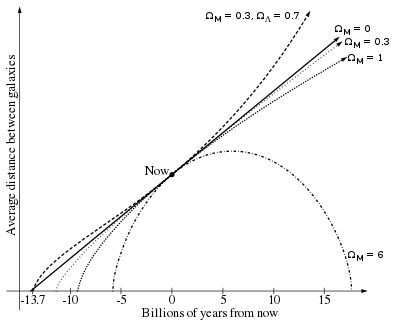

우주의 나이를 결정하는 문제는 ΛCDM 모형의 매개변수들을 결정하는 문제와 직결되어 있다. 표준모형에서 우주는 평범한 중입자 물질, 암흑 물질, 복사(전자기파와 중성미자를 포함), 그리고 암흑 에너지로 이루어져 있다. 밀도변수란 이 각각의 성분들이 우주의 전체 에너지 밀도에서 얼마나 많은 부분을 차지하는지를 나타낸다: (물질), (복사), (암흑에너지). 물론 ΛCDM 모형은 이 세가지 우주 변수들뿐만 아니라 다른 많은 변수들로 서술되지만, 우주의 나이를 결정하기 위해서는 이 세 우주변수(, , )와 함께 허블상수 가 가장 중요한 역할을 한다.
일단 이 우주 변수들을 정확하게 측정하면, 우주의 나이는 프리드만 방정식을 통해서 구할 수 있다. 이 방정식은 우주의 팽창율의 시간에 따른 변화와 우주의 물질구성(우주 밀도 변수들) 사이의 관계를 나타내는 식이다. 따라서 이 방정식을 시간에 대하여 푼 뒤. 적분을 하게 되면 다음과 같이 우주의 나이 ()를 밀도 변수와 허블상수로 표현할 수 있다.
여기서 는 허블 상수이고 함수 는 오로지 , , 에 의해서만 결정된다. 이 식에서 바로 알 수 있듯이 우주의 나이는 허블 상수의 역수()와, 다른 세 밀도변수에 따라 결정되는 보정항()의 곱으로 결정된다. 따라서 일단 우주의 나이는 허블 상수의 역수인 허블시간 = 로 근사값을 추정할 수 있다. 허블 상수()는 지금 현재 우주가 얼마나 빨리 팽창하고 있는가를 나타내며, 보통 (km/s/Mpc)의 단위로 표현된다. 허블의 법칙에 따르면 모든 은하는 거리에 비례하는 속도로 멀어지고 있으며, 그 비례상수가 허블 상수다. 천문학자들은 주로 거리는 Mpc 단위로 팽창 속도는 km/s 단위로 측정한다. 우주의 팽창속도가 항상 "일정"할 경우, 이 허블시간 만큼의 과거에는 모든 은하가 하나의 지점에 모인 것이 된다. 1 메가파섹 (Mpc) = 3.0856×1019 km이며, 만약 = 71 km/s/Mpc이면, = 2.30×10−18s−1, 따라서 허블시간은 4.35×1017초 또는 138 억 년이 된다.[4]
보다 정확한 우주의 나이를 구하려면, 과거 우주의 팽창률 변화를 서술하는 보정항 를 구해야 한다. 이 값은 수치 계산으로 구할 수 있으며, 여러 우주 변수들의 값에 따른 값들이 그림에 나와있다. 이 그림은 값을 일정하다고 보고, 와 값들을 바꿀때 값이 어떻게 변하는지를 계산한 것이다. 현재 받아 들여지고 있는 WMAP 값들 = (0.266, 0.732)을 대입하면 거의 1에 가까운 을 얻을 수 있다. 한편, 우수상수를 포함하지 않는 평평한 우주(flat universe)는 = (1.0, 0.0)을 가지며, 이 때는 가 되어 실제 우주의 나이는 앞에서 간단히 추정한 허블시간보다 젊어지게 된다.
WMAP 위성은 와[5] 값을[6] 아주 정확히 결정함으로써 우주의 나이를 구하는데 있어서 결정적인 기여를 하였다. 한편 허블 상수 값은 Ia형 초신성관측을 통해 상당히 정확한 값들을 얻을 수 있다.[출처 필요] 이 우주 변수들의 값과 허블상수값들로부터 일반적으로 받아들여지는 우주의 나이(137.5억년)가 얻어졌다.
우주의 나이 결정에서 0이 아닌 우주 상수()값은 우주의 나이를 좀 더 많게 만들었다. 우주 상수 또는 암흑 에너지의 존재가 알려지기 이 전에 표준모형은 한때 왜 우리은하내의 구상성단들의 나이가 왜 이렇게 구해진 우주의 나이보다 더 많은가를 설명할 수 없었으나, 우주 마이크로파 배경과 초신성 관측을 통해 정확한 를 측정함으로써 지금은 이러한 우주나이 위기 문제는 완전히 해결되었다.[7] [8]
WMAP 관측[편집]
2013년 기준으로, 9년에 걸친 NASA의 WMAP 관측으로부터 우주의 나이는 137.72±0.59억년으로 결정된 상태이다.[9] 물론 이 결과는 이 프로젝트의 계산 모형이 옳다는 것을 가정하고 있으며, 다른 방법으로 우주의 나이를 계산하면 약간 다른 나이나 정확도를 얻을 수도 있다. 예를 들면 상대론적 입자 때문에 생기는 배경을 가정한다면, 우주의 나이의 오차 범위가 최대 10배까지 커 질 수 있다는 주장도 있다.[10] WMAP에 의한 우주 변수 결정 (따라서 나이 결정)은 우주 마이크로파 배경 파워스펙트럼에서 첫 번째 acoustic peak의 위치로부터 "마지막 산란면"의 크기를 측정하는 방법을 통해 이루어진다. 이 마지막 산란면의 크기는 재결합시기의 우주의 크기와도 같다.[11]
역사[편집]
18세기에 들어서야 지구의 나이가 수 백만 년, 많게는 수 십억 년일지도 모른다는 생각이 나타나기 시작했다. 그러나 19세기부터 20세기 초까지만 하더라도 대부분의 과학자들은 비록 지역적으로는 별들이 새로 만들어지고 또 사라지기도 하지만, 전체적으로 보면 우주의 나이는 무한하며 우주는 영원히 정상상태에 있을 것이라고 믿고 있었다.
우주의 나이가 무한할 수 없을 것이라는 가정을 처음으로 제시한 것은 19세기 중반에 완성된 열역학이었다. "닫힌 계의 엔트로피는 항상 증가한다"는 열역학의 개념에 따르면, 만약 우주의 나이가 무한하다면 그 안에 있는 모든 것들의 온도는 똑같아야 하며, 따라서 우주에 별이나 생명 같은 것은 존재 할 수 없게 된다는 모순이 발생한다. 하지만 당시에는 아무도 이러한 모순을 해소할만한 설명을 제시하지 못했다. 1915년에 마침내 알베르트 아인슈타인이 일반상대론을 발표했다.[12] 이 이론을 바탕으로 조르주 르메트르는 우주는 결코 정지해 있을 수 없으며, 반드시 팽창하거나 수축하거나 해야 한다는 것을 보였다. 하지만 아인슈타인 자신은 우주가 정상상태에 있을 것이라고 믿었기 때문에, 자신의 방정식에 소위 우주상수라는 항을 추가해서 방정식이 정상상태 우주와 일치하도록 만들었다.
우주가 유한하다는 첫 번째 증거를 제시한 사람은 천문학자 에드윈 허블이었다.[13] 20세기 들어, 허블을 비롯한 천문학자들은 당시에 "나선성운"으로 알려졌던 천체들이 사실은 우리은하 밖에 존재하는 별개의 외부은하들이라는 것을 발견했다. 더욱이 이 은하들은 매우 멀리 떨어져 있으며, 이 은하들의 스펙트럼을 찍어본 결과 선 스펙트럼이 실험실에서 보다 긴 파장으로 관측되는 적색편이(redshift)를 발견했다. 이는 은하들이 우리로부터 멀어지고 있다는 것을 의미한다. 또한 멀리 떨어져 있는 은하일수록 더 큰 적색편이를 보였고, 따라서 더 빨리 우리로부터 멀어지고 있었다. 바로 이 사실이 우주가 정지해있지 않고 팽창하고 있다는 첫 관측적 증거가 되었다. 시간을 거꾸로 돌릴 경우 과거 어느 순간에는 우주의 모든 은하가 한 점으로 수렴하는 순간이 존재하여, 이는 우주에 시작이 있었고, 우주의 나이가 유한함을 의미한다. 허블은 현재의 팽창속도로부터 우주가 언제 팽창하기 시작했는지 계산함으로써 최초로 우주의 나이를 결정할 수 있었다. 허블이 처음으로 계산해낸 값은 우리가 지금 알고 있는 값 보다는 매우 작았는데, 이는 그 당시의 은하까지의 거리를 실제보다 가깝게 측정했었기 때문이다.
우주의 나이를 구하는 데 필요한 우주의 팽창속도(허블상수)를 제대로 측정해 낸 사람은 천문학자 앨런 샌디지이다.[14] 1958년에 그가 측정한 허블상수는 우리가 현재 알고 있는 우주의 나이와 상당히 비슷한 값을 도출하였지만, 그는 그 자신의 결과를 신뢰하지 않았다. 이는 당시에 가장 오래된 별들의 나이가 약 250억년이라고 알려져 있었고 우주의 나이는 이보다 당연히 커야 하기 때문이었다. 따라서 샌디지와 일단의 천문학자들은 계속 측정을 반복하면서, 관측된 허블상수값을 줄이기 위해 (따라서 우주의 나이를 늘리기 위해) 많은 노력을 하였다. 하지만 이 문제는 결국 별들의 나이 측정에 사용된 항성진화이론들이 점점 발전하고, 별들의 나이가 실제보다 많게 측정되었다는 것이 밝혀지며 해결되었다. 현재 가장 나이가 많은 별의 나이는 약 132억년이다.[15]
우주 마이크로파 배경의 발견(1965년) [16] 은 우주의 팽창에 대한 결정적인 증거가 되었고, 우주의 나이를 정확하게 측정하는 방법을 제공하였다. 2001년에 발사된 WMAP위성은 수 년에 걸쳐 우주 마이크로파 배경을 정밀하게 관측함으로써 허블 상수와 우주의 나이를 매우 정확하게 결정할 수 있도록 기여하였다.[11]
같이 보기[편집]
참고 문헌[편집]
- ↑ 가 나 Ade, P. A. R.; N. Aghanim, C. Armitage-Caplan, M. Arnaud, M. Ashdown, F. Atrio-Barandela, J. Aumont, C. Baccigalupi, A. J. Banday, R. B. Barreiro, J. G. Bartlett, E. Battaner, K. Benabed, A. Benoît, A. Benoit-Lévy, J.-P. Bernard, M. Bersanelli, P. Bielewicz, J. Bobin, J. J. Bock, A. Bonaldi, J. R. Bond, J. Borrill, F. R. Bouchet, M. Bridges, M. Bucher, C. Burigana, R. C. Butler, E. Calabrese, B. Cappellini, J.-F. Cardoso, A. Catalano, A. Challinor, A. Chamballu, R.-R. Chary, X. Chen, L.-Y Chiang, H. C. Chiang, P. R. Christensen, S. Church, D. L. Clements, S. Colombi, L. P. L. Colombo, F. Couchot, A. Coulais, B. P. Crill, A. Curto, F. Cuttaia, L. Danese, R. D. Davies, R. J. Davis, P. de Bernardis, A. de Rosa, G. de Zotti, J. Delabrouille, J.-M. Delouis, F.-X. Désert, C. Dickinson, J. M. Diego, K. Dolag, H. Dole, S. Donzelli, O. Doré, M. Douspis, J. Dunkley, X. Dupac, G. Efstathiou, F. Elsner, T. A. Enßlin, H. K. Eriksen, F. Finelli, O. Forni, M. Frailis, A. A. Fraisse, E. Franceschi, T. C. Gaier, S. Galeotta, S. Galli, K. Ganga, M. Giard, G. Giardino, Y. Giraud-Héraud, E. Gjerløw, J. González-Nuevo, K. M. Górski, S. Gratton, A. Gregorio, A. Gruppuso, J. E. Gudmundsson, J. Haissinski, J. Hamann, F. K. Hansen, D. Hanson, D. Harrison, S. Henrot-Versillé, C. Hernández-Monteagudo, D. Herranz, S. R. Hildebrandt, E. Hivon, M. Hobson, W. A. Holmes, A. Hornstrup, Z. Hou, W. Hovest, K. M. Huffenberger, T. R. Jaffe, A. H. Jaffe, J. Jewell, W. C. Jones, M. Juvela, E. Keihänen, R. Keskitalo, T. S. Kisner, R. Kneissl, J. Knoche, L. Knox, M. Kunz, H. Kurki-Suonio, G. Lagache, A. Lähteenmäki, J.-M. Lamarre, A. Lasenby, M. Lattanzi, R. J. Laureijs, C. R. Lawrence, S. Leach, J. P. Leahy, R. Leonardi, J. León-Tavares, J. Lesgourgues, A. Lewis, M. Liguori, P. B. Lilje, M. Linden-Vørnle, M. López-Caniego, P. M. Lubin, J. F. Macías-Pérez, B. Maffei, D. Maino, N. Mandolesi, M. Maris, D. J. Marshall, P. G. Martin, E. Martínez-González, S. Masi, S. Matarrese, F. Matthai, P. Mazzotta, P. R. Meinhold, A. Melchiorri, J.-B. Melin, L. Mendes, E. Menegoni, A. Mennella, M. Migliaccio, M. Millea, S. Mitra, M.-A. Miville-Deschênes, A. Moneti, L. Montier, G. Morgante, D. Mortlock, A. Moss, D. Munshi, P. Naselsky, F. Nati, P. Natoli, C. B. Netterfield, H. U. Nørgaard-Nielsen, F. Noviello, D. Novikov, I. Novikov, I. J. O'Dwyer, S. Osborne, C. A. Oxborrow, F. Paci, L. Pagano, F. Pajot, D. Paoletti, B. Partridge, F. Pasian, G. Patanchon, D. Pearson, T. J. Pearson, H. V. Peiris, O. Perdereau, L. Perotto, F. Perrotta, V. Pettorino, F. Piacentini, M. Piat, E. Pierpaoli, D. Pietrobon, S. Plaszczynski, P. Platania, E. Pointecouteau, G. Polenta, N. Ponthieu, L. Popa, T. Poutanen, G. W. Pratt, G. Prézeau, S. Prunet, J.-L. Puget, J. P. Rachen, W. T. Reach, R. Rebolo, M. Reinecke, M. Remazeilles, C. Renault, S. Ricciardi, T. Riller, I. Ristorcelli, G. Rocha, C. Rosset, G. Roudier, M. Rowan-Robinson, J. A. Rubiño-Martín, B. Rusholme, M. Sandri, D. Santos, M. Savelainen, G. Savini, D. Scott, M. D. Seiffert, E. P. S. Shellard, L. D. Spencer, J.-L. Starck, V. Stolyarov, R. Stompor, R. Sudiwala, R. Sunyaev, F. Sureau, D. Sutton, A.-S. Suur-Uski, J.-F. Sygnet, J. A. Tauber, D. Tavagnacco, L. Terenzi, L. Toffolatti, M. Tomasi, M. Tristram, M. Tucci, J. Tuovinen, M. Türler, G. Umana, L. Valenziano, J. Valiviita, B. Van Tent, P. Vielva, F. Villa, N. Vittorio, L. A. Wade, B. D. Wandelt, I. K. Wehus, M. White, S. D. M. White, A. Wilkinson, D. Yvon, A. Zacchei, A. Zonca (2013). “Planck 2013 results. I. Overview of products and scientific results”. arXiv:1303.5062. Bibcode:2013arXiv1303.5062P.
- ↑ “Cosmic Microwave Background Radiation”. 《History of Cosmology》. British Broadcasting Co. UK. 2011년 5월 13일에 원본 문서에서 보존된 문서. 2011년 3월 9일에 확인함.
- ↑ Chang, Kenneth (2008년 3월 9일). “Gauging Age of Universe Becomes More Precise”. 《The New York Times》.
- ↑ Liddle, Andrew R. (2003). 《An Introduction to Modern Cosmology》 2판. Chichester: Wiley. 57쪽. ISBN 0470848359.
- ↑ “Animation: Matter Content Sensitivity. The matter-radiation ratio is raised while keeping all other parameters fixed (Omega 0h^2= 0.1-1)”. uchicago.edu. 2008년 2월 23일에 원본 문서에서 보존된 문서. 2008년 2월 23일에 확인함.
- ↑ “Animation:Angular diameter distance scaling with curvature and lambda (Omega K=1-Omega 0-Omega Lambda, fixed Omega 0h^2 and Omega Bh^2)”. uchicago.edu. 2008년 2월 23일에 원본 문서에서 보존된 문서. 2008년 2월 23일에 확인함.
- ↑ “Independent age estimates”. astro.ubc.ca. 2008년 3월 6일에 원본 문서에서 보존된 문서. 2008년 2월 23일에 확인함.
- ↑ J. P. Ostriker; Paul J. Steinhardt (1995). “Cosmic concordance”: 5066. arXiv:astro-ph/9505066. Bibcode:1995astro.ph..5066O.
- ↑ Hinshaw, G.F.; 외. (2012). “Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Final Maps and Results”. 《ApJS》. arXiv:1212.5225.
- ↑ Francesco de Bernardis; A. Melchiorri, L. Verde, R. Jimenez (2008). “The Cosmic Neutrino Background and the age of the Universe”. 《Journal of Cosmology and Astroparticle Physics》 2008 (3): 020. arXiv:0707.4170. Bibcode:2008JCAP...03..020D. doi:10.1088/1475-7516/2008/03/020.
- ↑ 가 나 Spergel, D. N. (2003). “First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters”. 《The Astrophysical Journal Supplement Series》 148 (1): 175–194. arXiv:astro-ph/0302209. Bibcode:2003ApJS..148..175S. doi:10.1086/377226.
- ↑ Einstein, Albert (1915). “Zur allgemeinen Relativitätstheorie”. 《Sitzungsberichte der Königlich Preußischen Akademie der Wissensch》 (독일어): 778–786. Bibcode:1915SPAW.......778E.
- ↑ Hubble, Edwin (1929년 3월 15일). “A RELATION BETWEEN DISTANCE AND RADIAL VELOCITY AMONG EXTRA-GALACTIC NEBULAE”. 《PNAS》 15 (3): 168–173. Bibcode:1929PNAS...15..168H. doi:10.1073/pnas.15.3.168. PMC 522427. PMID 16577160. 2008년 6월 30일에 원본 문서에서 보존된 문서.
- ↑ Sandage, A. R. (May, 1958). “Current Problems in the Extragalactic Distance Scale”. 《Astrophysical Journal》 127 (3): 513–526. Bibcode:1958ApJ...127..513S. doi:10.1086/146483.
- ↑ Frebel, Anna; 외. (May, 2007). “Discovery of HE 1523-0901, a Strongly r-Process-enhanced Metal-poor Star with Detected Uranium”. 《Astrophysical Journal Letters》 660 (2): L117–L120. arXiv:astro-ph/0703414. Bibcode:2007ApJ...660L.117F. doi:10.1086/518122.
- ↑ Penzias, A.A.; Wilson, R.W. (July, 1965). “A Measurement of Excess Antenna Temperature at 4080 Mc/s”. 《Astrophysical Journal》 142: 419–421. Bibcode:1965ApJ...142..419P. doi:10.1086/148307.
외부 링크[편집]
- (영어) Ned Wright's Cosmology Tutorial
- (영어) Wayne Hu's cosmological parameter animations
- (영어) 구상성단 Archived 2008년 2월 24일 - 웨이백 머신
- (영어) 우주의 나이를 측정하는 여러 방법들
- (영어) 우주와 인류 역사의 중요한 사건을 일 년에 비유해서 서술함.
- (영어) iCosmos: Cosmology Calculator
- (영어) The Expanding Universe Archived 2013년 12월 5일 - 웨이백 머신 (American Institute of Physics)














