모스 이론
미분위상수학에서 모스 이론(Morse理論, 영어: Morse theory)은 다양체의 위상수학을 그 위에 정의된 매끄러운 함수로 분석하는 분야이다.[1][2][3][4][5][6][7][8] 이 경우 함수의 임계점을 통해 콤팩트 매끄러운 다양체 의 호몰로지를 모스 이론으로 구성할 수 있다. 이 구성을 모스 호몰로지라고 한다.
정의[편집]
모스 지표[편집]
이 매끄러운 다양체라고 하고, 그 위에 매끄러운 함수 이 있다고 하자. 의 임계점들은 의 기울기가 0인 의 부분 집합이다. 이를
로 표기하자.
에 속하는 의 부분 다양체
가 주어졌다고 하자. 그렇다면, 의 접다발을 어떤 임의의 리만 계량을 사용하여 위에서 접다발과 법다발로 분해할 수 있다.
(물론, 만약 가 한원소 공간일 경우, 이며 이다.)
이 경우, 및 그 근방의 국소 좌표계에 대하여, 헤세 행렬
을 정의할 수 있으며, 이를 에 제한할 수 있다. 이 경우, 의 에 대한 모스-보트 지표(Morse-Bott指標, 영어: Morse–Bott index) 는 의 음의 고윳값의 수이다. (이는 사용한 국소 좌표계 및 의 선택 및 리만 계량에 의존하지 않는다.) 특히, 만약 인 경우, 는 단순히 헤세 행렬 의 음의 고윳값의 수이다. 이를 라고 쓰며, 의 에서의 모스 지표(Morse指標, 영어: Morse index)라고 한다.
모스 함수와 모스-보트 함수[편집]
매끄러운 함수 가 다음 조건들을 만족시킨다면, 를 모스-보트 함수(Morse-Bott函數, 영어: Morse–Bott function)라고 한다.[9]:Definition 3.1
- 는 의 부분 다양체들의 합집합이다. (각 연결 성분들은 서로 다른 차원을 가질 수 있으나, 이들은 맞닿을 수 없다.)
- 의 임의의 연결 성분 를 골랐을 때, 모든 에 대하여 제한된 헤세 행렬 는 비퇴화 쌍선형 형식이다. 이 경우, 의 모스-보트 지표(Morse-Bott指標, 영어: Morse–Bott index) 는 의 음의 고윳값의 수이다. (이는 에 의존하지 않는다.)
이 경우, 각 를 의 임계 부분 다양체(臨界部分多樣體, 영어: critical submanifold)라고 한다.
또한, 매끄러운 함수 에 대하여 다음 두 조건이 서로 동치이며, 이를 만족시키는 함수를 모스 함수라고 한다.
- 모스 함수(Morse函數, 영어: Morse function)는 모든 임계점들의 헤세 행렬이 비퇴화 쌍선형 형식인 함수다. 즉, 헤세 행렬이 0을 고윳값으로 갖지 않는다.
- 의 모든 연결 성분이 0차원인 모스-보트 함수이다.
성질[편집]
모스 함수의 조밀성[편집]
매끄러운 함수 의 공간 위에 임의의 리만 계량을 가해, 다음과 같은 일련의 노름들로 프레셰 공간의 구조를 줄 수 있다.
이 프레셰 위상을 위상이라고 하고, 이는 사실 사용된 리만 계량에 의존하지 않는다.
이 위상에서, 모스 함수들의 부분 공간은 의 조밀 집합을 이룬다.
모스 세포 구조[편집]
다음이 주어졌다고 하자.
그렇다면, 각 에 대하여 부분 공간
을 정의할 수 있다. 이는 사실 경계다양체를 이룬다.
그렇다면, 임의의 , 에 대하여, 다음이 성립한다.
- 만약 이 의 임계점을 포함하지 않는다면, 와 는 서로 미분 동형이다.
- 만약 이 의 임계점 가운데 하나 를 포함하며, 또한 가 이외의 다른 임계점을 포함하지 않는다면, 는 에 차 세포를 추가한 공간과 호모토피 동치이다.
따라서, 만약 서로 다른 두 임계점에 대하여 의 값이 항상 서로 다르다면, 는 모스 함수 는 다양체 와 호모토피 동치인 세포 복합체를 결정짓는다. 이 세포 복합체에서 지표가 인 특이점은 차 세포에 대응된다. 또한, 모든 매끄러운 다양체에 대하여 이와 같은 꼴의 모스 함수를 찾을 수 있음을 보일 수 있다.
| 모스 이론 | 세포 복합체 |
|---|---|
| 모스 함수의 임계점 | 세포 |
| 모스 함수의 임계점의 모스 지표 | 세포의 차수 |
| (는 임계값이 아님) | 인 임계점들 에 대응하는 세포들로 구성된 뼈대 |
모스 부등식[편집]
매끄러운 다양체 위의 모스-보트 함수 가 주어졌다고 하면, 다음과 같은 모스-보트 다항식(영어: Morse–Bott polynomial)을 정의할 수 있다.[9]:Definition 3.4
이는 물론 모스 다항식의 일반화이다. 만약 가 모스 함수일 경우, 이를 모스 다항식(영어: Morse polynomial)이라고 한다.
이제, 이 콤팩트 가향 다양체이며, 각 또한 모두 가향 다양체라고 하자. (만약 가 모스 함수라면, 둘째 조건은 자명하게 성립한다.) 그렇다면, 모스-보트 부등식에 따르면,
가 되는, 자연수(음이 아닌 정수) 계수의 다항식
이 존재한다.[9]:Theorem 3.5
여기서
는 의 푸앵카레 다항식이다.
특히, 만약 일 경우
이 된다. 여기서 은 오일러 지표이다. (만약 가 모스 함수일 때, 이 사실은 세포 복합체의 세포 호몰로지로부터 간단하게 알 수 있다.)
가 모스 함수일 때, 위 다항식을 차수별로 분해하면,
이다. 즉, 차 임계점의 수는 차 베티 수의 상계를 이룬다. (이 역시 세포 복합체의 세포 호몰로지로부터 간단하게 알 수 있다.)
예[편집]
초구[편집]
차원 유클리드 공간 속의 표준적 (반지름 1의) 차원 초구
를 생각하자. 이 경우, 높이 는 모스 함수를 이루며, 이는 두 개의 임계점
을 가지며, 는 북극, 는 남극에 해당한다. 이 경우, 의 모스 지표는 이며, 의 모스 지표는 0이다. 이로부터 정의되는 세포 복합체 구조는 하나의 0차원 세포(남극) 및 하나의 차원 세포(남극을 제외한 모든 점)으로 구성된다.
수직 원환면[편집]
2차원 원환면 을 3차원 유클리드 공간에 다음과 같이 매장하였을 때, 높이 함수는 모스 함수를 이룬다.
이는 네 개의 임계점을 가지며, 그 지표는 (아래서부터) 각각 0, 1, 1, 2이다. 이는 원환면의 다음과 같은 세포 복합체 구조를 정의한다. 우선,
이다. 임의의 두 점 을 골랐을 때,
는 원환면의 세포 복합체를 정의하며, 이는 위의 모스 함수를 통하여 얻은 것과 동치이다.
보다 일반적으로, 종수 의 콤팩트 가향 곡면 를 위와 같이 배치하자. 그렇다면, 높이 함수는 모스 함수이며, 이는 개의 임계점을 갖는다. 이를 각각 순서대로 라고 할 때,
이다. 이것이 정의하는 세포 복합체 구조에서, 는 의 표준적 기저에 해당한다.
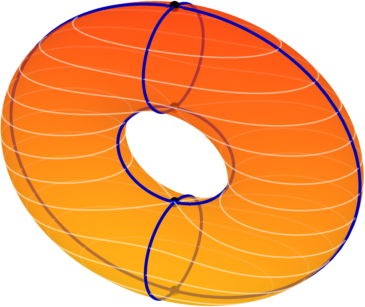
수평 원환면[편집]
반대로, 2차원 원환면을 3차원 유클리드 공간 속에서, xy 평면에 회전 대칭을 갖도록 매장하자. 이 경우, z방향 높이는 모스 함수를 이루지 못하지만, 모스-보트 함수를 이룬다. 이 경우 두 개의 임계 부분 다양체 가 존재한다. 이 경우
- 는 “남극”에 있는 원이며, 그 모스-보트 지표는 0이다.
- 는 “북극”에 있는 원이며, 그 모스-보트 지표는 1이다.
원의 푸앵카레 대항식은
이므로, 이 모스-보트 함수의 모스-보트 다항식은
이다. 원환면의 푸앵카레 다항식은
이므로, 이 경우 모스-보트 부등식이 포화된다 (즉, 이다).
모스 함수가 아닌 함수[편집]
1차원 이상의 매끄러운 다양체 위에서, 상수 함수를 생각하자. 이 경우 모든 점이 임계점이며, 모든 임계점의 헤세 행렬은 0이다. 그러므로 이는 모스 함수가 되지 못한다. (그러나 0차원 다양체(즉, 이산 공간)의 경우 이는 모스 함수를 이룬다.)
임의의 다양체 , 및 위의 함수 에 대하여, 위에 를 정의할 수 있다. 만약 이 1차원 이상이라면, 이는 항상 모스 함수가 아니다. 그러나 만약 가 모스 함수라면 는 모스-보트 함수를 이룬다.
역사와 어원[편집]
마스턴 모스 이전에도 이미 아서 케일리[10]와 제임스 클러크 맥스웰[11] 등이 측량학에 관련하여, 곡면 위에 정의된 높이 함수의 특이점들을 고려하였다.
마스턴 모스가 변분법을 연구하면서 모스 이론을 1934년 도입하였다.[12] 이후 모스는 평생을 주로 모스 이론을 연구하는 데 바쳤다.
이후 스티븐 스메일 · 라울 보트 · 에드워드 위튼 등이 모스 이론에 공헌하였다.
참고 문헌[편집]
- ↑ Matsumoto, Yukio (2002). 《An Introduction to Morse Theory》. Iwanami Series in Modern Mathematics (영어). American Mathematical Society. ISBN 978-0-8218-1022-4. MR 1873233.
- ↑ Nicolaescu, Liviu (2011). 《An Invitation to Morse Theory》. Universitext (영어) 2판. Springer. doi:10.1007/978-1-4614-1105-5. ISBN 978-1-4614-1104-8. ISSN 0172-5939. MR 2883440.
- ↑ Bott, Raoul (1982년 9월). “Lectures on Morse theory, old and new”. 《Bulletin of the American Mathematical Society (new series)》 (영어) 7 (2): 331–358. doi:10.1090/S0273-0979-1982-15038-8. ISSN 0273-0979. MR 663786.
- ↑ Bott, Raoul (1988). “Morse theory indomitable”. 《Publications Mathématiques de l'Institut des Hautes Études Scientifiques》 (영어) 68 (1): 99–114. doi:10.1007/BF02698544. ISSN 0073-8301. MR 1001450.
- ↑ Freed, Daniel S. (2011). “Commentary on “Lectures on Morse theory, old and new””. 《Bulletin of the American Mathematical Society》 (영어) 48: 517–523. doi:10.1090/S0273-0979-2011-01349-0. ISSN 0273-0979. MR 2823021.
- ↑ Banyaga, Augustin; David Hurtubise (2004). 《Lectures on Morse Homology》. Kluwer Texts in the Mathematical Sciences (영어) 29. Kluwer. doi:10.1007/978-1-4020-2696-6. ISBN 978-1-4020-2695-9. ISSN 0927-4529. MR 2145196.
- ↑ Schwarz, Matthias (1993). 《Morse Homology》. Progress in Mathematics (영어) 111. Birkhäuser. doi:10.1007/978-3-0348-8577-5. ISBN 978-3-0348-9688-7. MR 1239174.
- ↑ Guest, Martin (2001). “Morse theory in the 1990’s” (영어). arXiv:math/0104155. Bibcode:2001math......4155G.
- ↑ 가 나 다 Hurtubise, David E. (2012). “Three approaches to Morse–Bott homology” (영어). arXiv:1208.5066.
- ↑ Cayley, Arthur (1859). “On Contour and Slope Lines”. 《Philosophical Magazine (series 4)》 (영어) 18 (120): 264-268. doi:10.1080/14786445908642760.
- ↑ Maxwell, James Clerk (1870). “On hills and dales”. 《Philosophical Magazine (series 4)》 (영어) 40 (269): 421–427. doi:10.1080/14786447008640422.
- ↑ Morse, Marston (1934). 《The Calculus of Variations in the Large》. American Mathematical Society Colloquium Publication (영어) 18. New York: American Mathematical Society. JFM 60.0450.01.
외부 링크[편집]
- “Morse theory”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
- “Morse inequalities”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
- “Morse function”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
- “Morse index”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
- “Morse lemma”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
- Weisstein, Eric Wolfgang. “Morse theory”. 《Wolfram MathWorld》 (영어). Wolfram Research.
- Weisstein, Eric Wolfgang. “Morse function”. 《Wolfram MathWorld》 (영어). Wolfram Research.
- “Morse theory”. 《nLab》 (영어).
- “Discrete Morse Theory”. 《nLab》 (영어).



























![{\displaystyle M^{a}=f^{-1}(-\infty ,a]\subseteq M}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b665b0f10ba7d2349a196cfd702ccbaf9899c9fd)


![{\displaystyle f^{-1}[a,b]\subseteq M}](https://wikimedia.org/api/rest_v1/media/math/render/svg/676f24dcf15a6a12aa68611c82e4fcf43f14c8ce)




![{\displaystyle f^{-1}[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0271b4e02a328dca4b40a34113c5dbcc74a2616f)







![{\displaystyle R(t)\in \mathbb {N} [t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/334c1ae1b048cd2e304c036ab2dcc5dee7cd7034)