피타고라스 정리

빗변을 변으로 하는 정사각형의 넓이는 나머지 두 변을 변으로 한 정사각형의 넓이의 합과 같다.

유클리드 기하학에서, 피타고라스 정리(문화어: 세 평방의 정리, 영어: Pythagorean theorem, Pythagoras' theorem)는 직각 삼각형의 빗변의 길이의 제곱이 나머지 두 변의 길이의 제곱의 합과 같다는 정리이다.

빗변의 길이를 $c$ , 나머지 두 변의 길이를 $a,b$ 라 하면 피타고라스 정리는 다음과 같은 방정식으로 쓸 수 있다.^[1]

a^{2}+b^{2}=c^{2}

위의 식을 만족시키는 세 양의 정수의 쌍을 피타고라스 삼조라고 한다. 피타고라스 정리는 고대부터 현대까지 다양한 방식으로 증명되었으며, 기하적인 증명부터 대수적인 증명까지 다양한 분야를 망라한, 가장 많은 증명을 가진 정리 중 하나이다.

피타고라스 정리는 유클리드 공간이나 유클리드 공간이 아닌 공간으로 일반화할 수 있다. 이때 대상은 직각 삼각형 외에 n차원 도형으로 일반화된다. 예를 들어 유클리드 공간에서 직교 좌표계가 주어지면, 서로 떨어져 있는 두 점 사이의 거리는 피타고라스 정리처럼 표현된다.

정리

직각 삼각형의 두 직각변(밑변과 높이)의 길이를 각각 $a,b$ , 빗변의 길이를 $c$ 라 하면 다음과 같은 관계가 성립한다.

a^{2}+b^{2}=c^{2}

즉, $c$ 의 제곱은 $a$ 와 $b$ 의 제곱의 합이다. 이는 $c$ 를 변으로 하는 정사각형의 넓이가 $a$ 를 변으로 하는 정사각형의 넓이와 $b$ 를 변으로 하는 정사각형의 넓이의 합과 같음을 의미한다.

변의 길이 계산과 끼인각의 판별

직각 삼각형에서 직각변의 길이를 알고 있다면 빗변의 길이는 피타고라스 정리에 제곱근을 취해 다음과 같이 계산할 수 있다.

c={\sqrt {a^{2}+b^{2}}}

비슷하게, 빗변과 한쪽 직각변의 길이가 알려진 경우 다른 쪽 변의 길이는 다음과 같이 계산할 수 있다.

a={\sqrt {c^{2}-b^{2}}}

또는

b={\sqrt {c^{2}-a^{2}}}

피타고라스 정리는 삼각형이 직각 삼각형인 경우에 대한 정리이므로, 직각 삼각형이 아닌 경우에는 이를 일반화한 코사인 법칙을 이용하여 변의 길이를 계산할 수 있다.

또한 빗변의 맞은편 각 $\angle C$ 에 대해, 다음이 성립한다.

a^{2}+b^{2}=c^{2}

이면,

\angle C

는 직각이다.

a^{2}+b^{2}<c^{2}

이면,

\angle C

는 둔각이다.

a^{2}+b^{2}>c^{2}

이면,

\angle C

는 예각이다.

피타고라스 삼조

피타고라스 정리의 방정식을 만족시키는 세 양의 정수의 쌍을 피타고라스 삼조라고 한다. 예를 들어, $(3,4,5)$ 는 피타고라스 수이다.

증명

피타고라스 정리를 증명하는 방법은 여러 가지가 있다.

대수적 증명

피타고라스 정리는 다음과 같이 대수적으로 증명할 수 있다. 먼저 위의 그림과 같이 직각변이 $a,b$ , 빗변이 $c$ 인 4개의 직각 삼각형을 적절히 배열하여 큰 정사각형을 만들 수 있다. 이 큰 정사각형은 $(a+b)$ 를 변으로 하므로 그 넓이는 $(a+b)^{2}$ 이다. 또한, 이는 $c$ 를 변으로 하는 작은 정사각형의 넓이 $c^{2}$ 와 직각 삼각형의 넓이 $\textstyle {\frac {1}{2}}ab$ 의 4배의 합과 같다.

(a+b)^{2}=c^{2}+4\cdot {\frac {1}{2}}ab=c^{2}+2ab

이를 정리하면 피타고라스 정리를 얻는다.

c^{2}=(a+b)^{2}-2ab=a^{2}+2ab+b^{2}-2ab=a^{2}+b^{2}

삼각형의 닮음을 통한 증명

피타고라스 정리는 삼각형의 닮음을 사용하여 다음과 같이 증명할 수 있다.

그림에서, $CH$ 는 $C$ 를 지나는 빗변 $AB$ 의 수선이다.

삼각형 $ACH$ 와 $ABC$ 는 각 $A$ 를 공유하는 직각 삼각형이므로, AA에 따라 서로 닮음이다. 마찬가지로, 삼각형 $CBH$ 와 $ABC$ 는 서로 닮음이다. 따라서, 대응변에 대한 비례식이 다음과 같이 성립한다.

{\frac {AC}{AH}}={\frac {AB}{AC}}

{\frac {BC}{BH}}={\frac {AB}{BC}}

즉, 다음이 성립한다.

AC^{2}=AB\cdot AH

BC^{2}=AB\cdot BH

이 두 식을 합하면 피타고라스 정리를 얻는다.

AC^{2}+BC^{2}=AB\cdot AH+AB\cdot BH=AB\cdot (AH+BH)=AB^{2}

유클리드의 증명

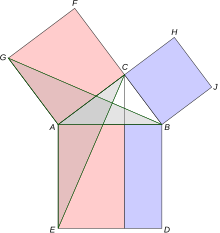
유클리드는 원론에서 피타고라스 정리를 다음과 같이 증명하였다.

그림에서, $ABDE$ 와 $ACFG$ , $BCHJ$ 는 모두 정사각형이다. $C$ 를 지나는 $AB$ 의 수선은 정사각형 $ABDE$ 를 직사각형 $AELM$ 과 $BDLM$ 으로 나눈다.

삼각형의 넓이는 '1/2 × 밑변 × 높이'이므로, 삼각형 $ABG$ 의 넓이는 정사각형 $ACFG$ 의 넓이의 절반이다. 마찬가지로, 삼각형 $AEC$ 의 넓이는 직사각형 $AELM$ 의 빨간색 부분의 넓이의 절반이다.

삼각형 $ABG$ 를 $A$ 를 중심으로 시계 방향으로 90도 회전하면 삼각형 $AEC$ 를 얻으므로, SAS에 따라 삼각형 $ABG$ 와 $AEC$ 는 합동이다. 서로 합동인 삼각형의 넓이는 같으므로, 삼각형 $ABG$ 와 $AEC$ 의 넓이는 같다.

따라서, 정사각형 $ACFG$ 의 넓이는 직사각형 $AELM$ 의 넓이와 같다. 마찬가지로, 정사각형 $BCHJ$ 의 넓이는 직사각형 $BDLM$ 의 넓이와 같다. 따라서, 정사각형 $ACFG$ 와 $BCHJ$ 의 넓이의 합은 정사각형 $ABDE$ 의 넓이와 같다.

가필드의 증명

미국의 20대 대통령 제임스 가필드는 다음과 같은 방법으로 피타고라스 정리를 증명했다.^[2]

두 평행한 변의 길이가 각각 $a,b$ 이고 이 두 변과 수직인 변의 길이가 $a+b$ 인 사다리꼴의 넓이는 다음 공식을 따른다.

$A={\frac {1}{2}}(a+b)^{2}={\frac {1}{2}}(a^{2}+2ab+b^{2})$

그림에서 삼각형 1, 2의 면적은 각각 ${\tfrac {1}{2}}ab$ 이고, 두 삼각형의 면적의 합은 $ab$ 이다.

삼각형 3의 면적은 $A-ab={\frac {1}{2}}(a^{2}+b^{2})={\frac {1}{2}}c^{2}$ 이므로

이를 정리하면 피타고라스 정리를 얻는다.

$a^{2}+b^{2}=c^{2}$

역

피타고라스 정리의 역 또한 성립한다. 즉, 만약 삼각형의 세 변 $a,b,c$ 가 $a^{2}+b^{2}=c^{2}$ 를 만족시킨다면, 이 삼각형은 반드시 $c$ 를 빗변으로 하는 직각 삼각형이다.

역의 증명

피타고라스 정리의 역은 다음과 같이 증명할 수 있다.

삼각형 $ABC$ 에서, $A,B,C$ 의 대변 $a,b,c$ 가 $a^{2}+b^{2}=c^{2}$ 를 만족시킨다고 하자.

임의의 점 $C'$ 을 취하자. $C'$ 를 꼭짓점으로 하는 직각을 그리자. 직각의 두 변에서 각각 적절한 $A',B'$ 를 취하여, $A'C'=AC=b$ 이며, $B'C'=BC=a$ 이도록 만들자.

그렇다면, $A'B'C'$ 는 $a,b$ 를 직각변으로 하는 직각 삼각형이다. 피타고라스 정리에 따라 그 빗변은 $c$ 이다. SSS에 따라 삼각형 $ABC$ 와 $A'B'C'$ 는 서로 합동이다. 따라서 각 $C$ 는 각 $C'$ 와 같이 직각이다. 즉, $ABC$ 는 $c$ 를 빗변으로 하는 직각 삼각형이다.

일반화

코사인 법칙

임의의 삼각형의 세 변 $a,b,c$ 사이에 다음과 같은 관계가 성립하며, 이를 코사인 법칙이라고 한다.

c^{2}=a^{2}+b^{2}-2ab\cos C

여기서

$C$ 는 $c$ 의 대각이다.
$\cos$ 는 코사인이다.

코사인 법칙에 $\textstyle C={\frac {\pi }{2}}=90^{\circ }$ 를 취하면 피타고라스 정리를 얻는다.

유클리드 거리

직교 좌표계의 두 점 $(x_{1},y_{1}),(x_{2},y_{2})\in \mathbb {R} ^{2}$ 사이의 거리는 다음과 같다.

{\sqrt {(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}}

보다 일반적으로, $n$ 차원 유클리드 공간 $\mathbb {R} ^{n}$ 의 두 점 $(a_{1},\dots ,a_{n}),(b_{1},\dots ,b_{n})\in \mathbb {R} ^{n}$ 사이의 거리는 다음과 같다.

{\sqrt {(a_{1}-b_{1})^{2}+\cdots +(a_{n}-b_{n})^{2}}}

노름 공간

내적 공간 $(V,\langle \cdot ,\cdot \rangle )$ 의 두 벡터 $v,w\in V$ 가 직교한다고 하자. (즉, $\langle v,w\rangle =0$ 이라고 하자.) 그렇다면, 이 두 원소의 노름과 둘의 합의 노름 사이에 다음과 같은 관계가 성립하며, 이를 노름 공간 위의 피타고라스 정리라고 한다.

\Vert v+w\Vert ^{2}=\Vert v\Vert ^{2}+\Vert w\Vert ^{2}

보다 일반적으로, $n$ 개의 벡터 $v_{1},\dots ,v_{n}\in V$ 가 쌍마다 직교한다고 하자. (즉, $\langle v_{i},v_{j}\rangle$ 가 대각 행렬을 이룬다고 하자.) 그렇다면, 이들의 노름과 합의 노름 사이에 다음과 같은 관계가 성립한다.

\Vert v_{1}+\cdots +v_{n}\Vert ^{2}=\Vert v_{1}\Vert ^{2}+\cdots +\Vert v_{n}\Vert ^{2}

역사

정리에 이름이 붙은 피타고라스는 기원전 570년경에 태어난 그리스 철학자이다. 그러나 정리는 피타고라스가 태어나기 훨씬 전부터 여러 문명에서 독립적으로 발견되고 사용되었다.

피타고라스 정리가 한 번 발견되었는지, 아니면 여러 장소에서 여러 번 발견되었는지에 대해서는 논쟁이 있으며, 최초의 발견 시기와 첫 증명 시기 또한 불확실하다. 이 정리의 역사는 피타고라스 삼조에 대한 지식, 직각삼각형의 변 사이의 관계에 대한 지식, 인접한 각 사이의 관계에 대한 지식, 그리고 어떤 연역 체계 내에서의 정리에 대한 증명 등 네 부분으로 나눌 수 있다.

기원전 1800년경에 작성된 이집트 중왕국 시대의 베를린 파피루스 6619에는 두 정사각형의 넓이의 합이 세 번째 정사각형의 넓이가 되는 문제와 그 해인 피타고라스 세 쌍인 6:8:10가 써있다. 다만 문제에서 삼각형을 언급하지는 않는다.^[3] 플루타르코스에 따르면, 고대 이집트인들은 3:4:5 직각삼각형을 알고 있었으며, 세 변을 각각 오시리스, 이시스, 호루스와 동일시했다.^[4]

메소포타미아 수학 역사학자들은 피타고라스의 규칙이 피타고라스가 태어나기 천 년 전인 구바빌로니아 시대(기원전 20세기~16세기)에 이미 널리 사용되었다고 결론지었다.^[6]^[7]^[8]^[9]

기원전 1800년경 라르사 근처에서 작성된 메소포타미아 점토판 플림톤 322에는 15개의 서로 다른 피타고라스 삼조가 적혀있다.^[10] 비슷한 시기의 또 다른 점토판인 YBC 7289에는 정사각형의 대각선, 즉 직각이등변삼각형의 빗변의 계산이 적혀있다.^[11]

인도에서는 기원전 8세기에서 5세기 사이로 추정되는^[12] Baudhayana Shulba Sutra에는 피타고라스 삼조의 목록과 피타고라스 정리에 대한 서술이 있다. 이는 직각이등변삼각형의 특수한 경우와 일반적인 경우 모두를 다루며, Apastamba Shulba Sutra(기원전 600년경)에서도 마찬가지로 나타난다.^[13]

피타고라스 학파는 피타고라스 삼조를 구하는 방법을 고안하였다. 즉, 홀수 $m$ 에 대하여, $\textstyle (m,{\frac {m^{2}-1}{2}},{\frac {m^{2}+1}{2}})$ 는 피타고라스 삼조이다. 또한, 피타고라스 학파의 히파소스는 이 과정에서 통약 불가능 비율을 발견하였다고 여겨진다.

에우클레이데스는 원론에서 피타고라스 정리를 서술 및 증명하였으며, 이는 발견된 최초의 증명이다.

인도인 역시 피타고라스 정리를 "직사각형의 대각선의 제곱은 두 이웃변의 제곱합과 같다"는 내용으로서 알고 있었다.^[14] 이는 적절한 모양의 제단을 만드는 데 응용되었다.^[15]

유휘는 《구장산술주》에서 원주율을 계산하는 데 피타고라스 정리를 사용하였다.

피타고라스 학파가 피타고라스 정리를 발견 및 증명하였는지는 확실하지 않다. 프로클로는 원론의 주해를 쓸 때, 정리의 발견과 최초 증명에 대한 공로를 피타고라스에게 돌렸다. 이에 대하여, 모리스 클라인은 다음과 같이 적었다.

“	[...] 그들[피타고라스 학파]이 피타고라스 정리를 증명하였었는지에 대해서는 널리 탐구되어 왔으며, 그에 대한 답은 그렇지 않을 수도 있다는 것이다. 닮음 삼각형을 사용한 증명은 상대적으로 쉬운 방법이나, 피타고라스 학파는 닮음 도형에 대한 완전한 이론을 갖지 못했다. 유클리드의 원론 제1권 명제 47에서의 증명은 닮음 도형 이론을 사용하지 않으므로, 어려운 증명이다. 또한, 프로클로는 이 증명의 공로를 유클리드에게 돌렸다. [...] The question of whether they [the Pythagoreans] proved the Pythagorean theorem has been extensively pursued, and the answer is that they probably did not. It is relatively easy to prove it by using facts about similar triangles, but the Pythagoreans did not have a complete theory of similar figures. The proof given in Proposition 47 of Book I of Euclid's Elements (Chap. 4, sec. 4) is a difficult one because it does not use the theory of similar figures, and this proof was credited by Proclus to Euclid himself.	”
	— ^[14]^{:34, §3.5}

같이 보기

위키미디어 공용에 피타고라스 정리 주제와 관련된 미디어 분류가 있습니다.

각주

↑ Judith D. Sally (2007). 〈Chapter 3: Pythagorean triples〉. 《Roots to research: a vertical development of mathematical problems》. American Mathematical Society Bookstore. 63쪽. ISBN 978-0-8218-4403-8.
↑ “Pythagorean Theorem and its many proofs”. 2019년 1월 30일에 확인함.
↑ Gillings, Richard J. (1982). 《Mathematics in the Time of the Pharaohs》. New York: Dover. 161쪽.
↑ Plutarch (1936). 《Moralia V: Isis and Osiris》. 번역 Babbitt, Frank Cole. Loeb Classical Library 306. Harvard University Press. 135쪽.
↑ Neugebauer 1969, 36쪽.
↑ Neugebauer 1969: p. 36 "In other words it was known during the whole duration of Babylonian mathematics that the sum of the squares on the lengths of the sides of a right triangle equals the square of the length of the hypotenuse."
↑ Friberg, Jöran (1981). “Methods and traditions of Babylonian mathematics: Plimpton 322, Pythagorean triples, and the Babylonian triangle parameter equations”. 《Historia Mathematica》 8: 277–318. doi:10.1016/0315-0860(81)90069-0. : p. 306 "Although Plimpton 322 is a unique text of its kind, there are several other known texts testifying that the Pythagorean theorem was well known to the mathematicians of the Old Babylonian period."
↑ Høyrup, Jens (1999). 〈Pythagorean 'Rule' and 'Theorem' – Mirror of the Relation Between Babylonian and Greek Mathematics〉. Renger, Johannes (편집). 《Babylon: Focus mesopotamischer Geschichte, Wiege früher Gelehrsamkeit, Mythos in der Moderne. 2. Internationales Colloquium der Deutschen Orient-Gesellschaft 24.–26. März 1998 in Berlin》 (PDF). Berlin: Deutsche Orient-Gesellschaft / Saarbrücken: SDV Saarbrücker Druckerei und Verlag. 393–407쪽. , p. 406, "To judge from this evidence alone it is therefore likely that the Pythagorean rule was discovered within the lay surveyors' environment, possibly as a spin-off from the problem treated in Db₂-146, somewhere between 2300 and 1825 BC." (Db₂-146 is an Old Babylonian clay tablet from Eshnunna concerning the computation of the sides of a rectangle given its area and diagonal.)
↑ Robson 2008, 109쪽: "Many Old Babylonian mathematical practitioners ... knew that the square on the diagonal of a right triangle had the same area as the sum of the squares on the length and width: that relationship is used in the worked solutions to word problems on cut-and-paste 'algebra' on seven different tablets, from Ešnuna, Sippar, Susa, and an unknown location in southern Babylonia."
↑ Robson 2001.
↑ Mackinnon, Nick (March 1992). “Homage to Babylonia”. 《The Mathematical Gazette》 76 (475): 158–178. doi:10.2307/3620389. JSTOR 3620389.
↑ Kim Plofker (2009). 《Mathematics in India》. Princeton University Press. 17–18쪽. ISBN 978-0-691-12067-6.
↑ Boyer & Merzbach (2011), 187쪽: "[In Sulba-sutras,] we find rules for the construction of right angles by means of triples of cords the lengths of which form Pythagorean triages, such as 3, 4, and 5, or 5, 12, and 13, or 8, 15, and 17, or 12, 35, and 37. Although Mesopotamian influence in the Sulvasũtras is not unlikely, we know of no conclusive evidence for or against this. Aspastamba knew that the square on the diagonal of a rectangle is equal to the sum of the squares on the two adjacent sides. Less easily explained is another rule given by Apastamba – one that strongly resembles some of the geometric algebra in Book II of Euclid's Elements. (...)"
1 2 Kline, Morris (1972). 《Mathematical Thoughts from Ancient to Modern Times. Volume 1》 (영어). New York, New York: Oxford University Press. ISBN 0-19-506135-7.
↑ Carl Benjamin Boyer; Uta C. Merzbach (2011). "China and India". A history of mathematics, 3rd Edition. Wiley. p. 229. ISBN 978-0470525487. Quote: [In Sulba-sutras,] we find rules for the construction of right angles by means of triples of cords the lengths of which form Pythagorean triages, such as 3, 4, and 5, or 5, 12, and 13, or 8, 15, and 17, or 12, 35, and 37. Although Mesopotamian influence in the Sulvasũtras is not unlikely, we know of no conclusive evidence for or against this. Aspastamba knew that the square on the diagonal of a rectangle is equal to the sum of the squares on the two adjacent sides. Less easily explained is another rule given by Apastamba – one that strongly resembles some of the geometric algebra in Book II of Euclid's Elements. (...)

외부 링크

Bogomolny, Alexander. “Pythagorean Theorem” (영어). 《Interactive Mathematics Miscellany and Puzzles》. 2018년 11월 10일에 확인함. (피타고라스 정리의 118여가지 증명법)
이철희. “피타고라스 정리”. 《수학노트》.
“Pythagorean theorem” (영어). 《Encyclopedia of Mathematics》. Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
Weisstein, Eric Wolfgang. “Pythagorean theorem” (영어). 《Wolfram MathWorld》. Wolfram Research.
“Pythagorean theorem” (영어). 《nLab》.
“Pythagorean theorem” (영어). 《PlanetMath》.
“Proof of Pythagorean theorem” (영어). 《PlanetMath》.
“Pythagoras's theorem” (영어). 《ProofWiki》.
“Pythagorean theorem (Hilbert space)” (영어). 《ProofWiki》.

[Sally0-1] Judith D. Sally (2007). 〈Chapter 3: Pythagorean triples〉. 《Roots to research: a vertical development of mathematical problems》. American Mathematical Society Bookstore. 63쪽. ISBN 978-0-8218-4403-8.

[2] “Pythagorean Theorem and its many proofs”. 2019년 1월 30일에 확인함.

[3] Gillings, Richard J. (1982). 《Mathematics in the Time of the Pharaohs》. New York: Dover. 161쪽.

[4] Plutarch (1936). 《Moralia V: Isis and Osiris》. 번역 Babbitt, Frank Cole. Loeb Classical Library 306. Harvard University Press. 135쪽.

[Neugebauer-5] Neugebauer 1969, 36쪽.

[6] Neugebauer 1969: p. 36 "In other words it was known during the whole duration of Babylonian mathematics that the sum of the squares on the lengths of the sides of a right triangle equals the square of the length of the hypotenuse."

[7] Friberg, Jöran (1981). “Methods and traditions of Babylonian mathematics: Plimpton 322, Pythagorean triples, and the Babylonian triangle parameter equations”. 《Historia Mathematica》 8: 277–318. doi:10.1016/0315-0860(81)90069-0. : p. 306 "Although Plimpton 322 is a unique text of its kind, there are several other known texts testifying that the Pythagorean theorem was well known to the mathematicians of the Old Babylonian period."

[8] Høyrup, Jens (1999). 〈Pythagorean 'Rule' and 'Theorem' – Mirror of the Relation Between Babylonian and Greek Mathematics〉. Renger, Johannes (편집). 《Babylon: Focus mesopotamischer Geschichte, Wiege früher Gelehrsamkeit, Mythos in der Moderne. 2. Internationales Colloquium der Deutschen Orient-Gesellschaft 24.–26. März 1998 in Berlin》 (PDF). Berlin: Deutsche Orient-Gesellschaft / Saarbrücken: SDV Saarbrücker Druckerei und Verlag. 393–407쪽. , p. 406, "To judge from this evidence alone it is therefore likely that the Pythagorean rule was discovered within the lay surveyors' environment, possibly as a spin-off from the problem treated in Db₂-146, somewhere between 2300 and 1825 BC." (Db₂-146 is an Old Babylonian clay tablet from Eshnunna concerning the computation of the sides of a rectangle given its area and diagonal.)

[9] Robson 2008, 109쪽: "Many Old Babylonian mathematical practitioners ... knew that the square on the diagonal of a right triangle had the same area as the sum of the squares on the length and width: that relationship is used in the worked solutions to word problems on cut-and-paste 'algebra' on seven different tablets, from Ešnuna, Sippar, Susa, and an unknown location in southern Babylonia."

[FOOTNOTERobson2001-10] Robson 2001.

[11] Mackinnon, Nick (March 1992). “Homage to Babylonia”. 《The Mathematical Gazette》 76 (475): 158–178. doi:10.2307/3620389. JSTOR 3620389.

[12] Kim Plofker (2009). 《Mathematics in India》. Princeton University Press. 17–18쪽. ISBN 978-0-691-12067-6.

[13] Boyer & Merzbach (2011), 187쪽: "[In Sulba-sutras,] we find rules for the construction of right angles by means of triples of cords the lengths of which form Pythagorean triages, such as 3, 4, and 5, or 5, 12, and 13, or 8, 15, and 17, or 12, 35, and 37. Although Mesopotamian influence in the Sulvasũtras is not unlikely, we know of no conclusive evidence for or against this. Aspastamba knew that the square on the diagonal of a rectangle is equal to the sum of the squares on the two adjacent sides. Less easily explained is another rule given by Apastamba – one that strongly resembles some of the geometric algebra in Book II of Euclid's Elements. (...)"

[Kline-14] 1 2 Kline, Morris (1972). 《Mathematical Thoughts from Ancient to Modern Times. Volume 1》 (영어). New York, New York: Oxford University Press. ISBN 0-19-506135-7.

[15] Carl Benjamin Boyer; Uta C. Merzbach (2011). "China and India". A history of mathematics, 3rd Edition. Wiley. p. 229. ISBN 978-0470525487. Quote: [In Sulba-sutras,] we find rules for the construction of right angles by means of triples of cords the lengths of which form Pythagorean triages, such as 3, 4, and 5, or 5, 12, and 13, or 8, 15, and 17, or 12, 35, and 37. Although Mesopotamian influence in the Sulvasũtras is not unlikely, we know of no conclusive evidence for or against this. Aspastamba knew that the square on the diagonal of a rectangle is equal to the sum of the squares on the two adjacent sides. Less easily explained is another rule given by Apastamba – one that strongly resembles some of the geometric algebra in Book II of Euclid's Elements. (...)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]