큰 십이면체

큰 십이면체
종류	케플러-푸앵소 다면체
별모양화 중심	정십이면체
원소	F = 12, E = 30 V = 12 (χ = -6)
면의 수{변의 수}	12{5}
슐레플리 기호	{5,5/2}
면 배치	V(5/2)5
위토프 기호	5/2 | 2 5
콕서터 다이어그램
대칭군	Ih, H3, [5,3], (*532)
참조	U35, C44, W21
특성	정다면체 비볼록
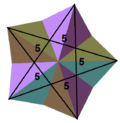(55)/2 (꼭짓점 도형)	작은 별모양 십이면체 (쌍대다면체)

기하학에서 큰 십이면체(great dodecahedron)는 슐레플리 기호가 {5,5/2}이고 콕서터 다이어그램이 인 케플러-푸앵소 다면체이다. 이것은 비볼록 정다면체 네 개 중 하나이다. 이것은 오각형 면 12개(평행한 오각형 여섯 쌍)로 이루어져 있으며, 각 꼭짓점에서 다섯 개의 오각형이 만나고, 서로를 오각성 모양을 만들며 교차한다.

큰 십이면체의 발견은 1810년에 종종 루이 푸앵소에 의해서 쓰여졌지만, 벤첼 얌니처에 의해 쓰여진 1568년의 책 Perspectiva Corporum Regularium에서 큰 십이면체와 매우 유사한 그림이 있다. 정십이면체의 별모양화중의 하나이며, 겉으로 드러난 부분만 뒤집으면 작은 삼각육변형 이십면체가 된다.

그림

투명 모형	구면 타일링
(애니메이션)	이 다면체는 밀도가 3인 구면 타일링을 나타낸다. (위에서 구면 오각형 면 하나를 노란색으로 칠했다)
전개도	별모양화
× 20 표면 기하학의 전개도; 이등변삼각형 삼각뿔 이십개를 정이십면체의 면처럼 배열해서 만들 수 있다.	이것은 정십이면체의 별모양화 세 개 중 두 번째를 만들 수 있고, 웨닝거 모델 [W21]을 가리킨다.

관련 다면체

이것은 볼록 정이십면체와 같은 모서리 배열을 가진다.

큰 십이면체가 적절한 교차 표면 기하학으로 고려되면, 이것은 볼록한 것 대신에 오목한 각뿔을 가지는 삼방이십면체와 같은 위상을 가진다. 파낸 십이면체는 정십이면체에 같은 과정을 적용한 것으로 볼 수 있다.

큰 십이면체에 적용된 깎는 과정은 일련의 비볼록 고른 다면체들을 만들어낸다. 깎아서 모서리가 점이 되면 절반 깎은 큰 십이면체처럼 십이십이면체를 만들어낸다. 이 과정은 원래 면이 점이 되도록 하는 birectification이 되면 끝나고 작은 별모양 십이면체를 만들어낸다.

정십이면체의 별모양화
플라톤의 다면체	케플러-푸앵소 다면체
정십이면체	작은 별모양 십이면체	큰 십이면체	큰 별모양 십이면체

이름	작은 별모양 십이면체	십이십이면체	깎은 큰 십이면체	큰 십이면체
콕서터 다이어그램
그림

활용

• 이 모양은 루빅스 큐브의 기본이 된다-알렉산더의 별 퍼즐 처럼.
• 큰 십이면체는 이진 골레 부호의 쉬운 기억법을 제공한다

같이 보기

• 작은 별모양 십이면체와 큰 십이면체의 결합물

외부 링크

• Weisstein, Eric Wolfgang. Great dodecahedron (Uniform polyhedron). 《Wolfram MathWorld》 (영어). Wolfram Research.
• Weisstein, Eric Wolfgang. “Three dodecahedron stellations”. 《Wolfram MathWorld》 (영어). Wolfram Research. 
• Uniform polyhedra and duals
• Metal sculpture of Great Dodecahedron