미분기하학에서, 리 준군(Lie準群, 영어: Lie groupoid)은 대상과 사상의 공간이 각각 매끄러운 다양체를 이루는 준군이다. (이산) 준군과 리 군의 공통적인 일반화이다.
리 준군은 매끄러운 다양체의 범주 속의 준군 대상이다. 즉, 구체적으로 다음과 같은 데이터로 주어진다.
- 매끄러운 다양체
 ,
, 
- 매끄러운 함수
 ,
,  . 이들은 사상의 정의역과 공역을 나타낸다.
. 이들은 사상의 정의역과 공역을 나타낸다.
- 사상의 합성

- 매끄러운 함수
 . 이는 항등 사상을 나타낸다.
. 이는 항등 사상을 나타낸다.
이 데이터는 준군의 공리들을 만족시켜야 한다.
마찬가지로, 리 2-준군(영어: Lie 2-groupoid), 리 3-준군(영어: Lie 3-groupoid) 등등을 정의할 수 있다. 예를 들어, 리 2-준군은 2-범주 가운데, 모든 1-사상과 2-사상이 가역원을 가지며, 또한 0-사상, 1-사상, 2-사상들이 각각 매끄러운 다양체  ,
,  ,
,  를 이루며, 정의에 등장하는 모든 사상들이 매끄러운 함수가 되는 경우이다.
를 이루며, 정의에 등장하는 모든 사상들이 매끄러운 함수가 되는 경우이다.
분류 공간[편집]
리 군  이 주어졌다고 하자. 그렇다면, 이를 하나의 대상만을 갖는 자명한 준군으로 여길 수 있으며, 이는 리 준군을 이룬다. 이를
이 주어졌다고 하자. 그렇다면, 이를 하나의 대상만을 갖는 자명한 준군으로 여길 수 있으며, 이는 리 준군을 이룬다. 이를  와 구별하기 위하여
와 구별하기 위하여  로 쓴다. (이에 대응하는 슈발레-에일렌베르크 대수를 설리번 대수로 여기면, 이에 대응하는 위상 공간은
로 쓴다. (이에 대응하는 슈발레-에일렌베르크 대수를 설리번 대수로 여기면, 이에 대응하는 위상 공간은  의 분류 공간이다.)
의 분류 공간이다.)
만약  가 아벨 리 군일 때는, 마찬가지로
가 아벨 리 군일 때는, 마찬가지로  ,
,  등등을 정의할 수 있다. 즉,
등등을 정의할 수 있다. 즉,  는 하나의 0-사상, 1-사상, ……, 하나의
는 하나의 0-사상, 1-사상, ……, 하나의  -사상을 가지며, 그
-사상을 가지며, 그  -사상의 매끄러운 다양체는
-사상의 매끄러운 다양체는  이다.
이다.
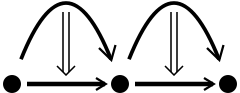
만약  가 아벨 군이 아니라면, 고차에서의 구성에서, 수평 합성이 수직 합성과 아래와 같이 가환해야 한다는 조건이 성립하지 못한다.
가 아벨 군이 아니라면, 고차에서의 구성에서, 수평 합성이 수직 합성과 아래와 같이 가환해야 한다는 조건이 성립하지 못한다.
|
=
|

|
=
|

|

|

|

|

|
체흐 준군[편집]
매끄러운 다양체  의 열린 덮개
의 열린 덮개  가 주어졌다고 하자. 그렇다면,
가 주어졌다고 하자. 그렇다면,  의 체흐 준군(영어: Čech groupoid)
의 체흐 준군(영어: Čech groupoid)  은 다음과 같은 리 준군이다.
은 다음과 같은 리 준군이다.
 의 대상들의 매끄러운 다양체는
의 대상들의 매끄러운 다양체는  이다. 즉, 그 대상은
이다. 즉, 그 대상은  가 되는 순서쌍
가 되는 순서쌍  이다.
이다. 의 사상들의 매끄러운 다양체는
의 사상들의 매끄러운 다양체는  이다. 즉, 사상
이다. 즉, 사상  은 순서쌍
은 순서쌍  이다.
이다.- 두 사상의 합성은 단순히
 이다.
이다.
- 항등 사상은 단순히
 의 꼴의 사상이다.
의 꼴의 사상이다.
그렇다면, 다음과 같은 함자가 존재한다.



(이 함자의 공역은 모든 사상이 항등 사상인 자명한 리 준군이다.)
보다 일반적으로, 임의의 양의 정수  에 대하여, 체흐
에 대하여, 체흐  -준군을 정의할 수 있다. 이 경우,
-준군을 정의할 수 있다. 이 경우,  -사상의 매끄러운 다양체는
-사상의 매끄러운 다양체는

이다.
순서쌍 리 군[편집]
임의의 매끄러운 다양체  에 대하여, 다음과 같은 순서쌍 리 준군(영어: pair Lie groupoid)을 정의할 수 있다.
에 대하여, 다음과 같은 순서쌍 리 준군(영어: pair Lie groupoid)을 정의할 수 있다.
- 그 대상(0-사상)의 매끄러운 다양체는
 이다.
이다.
- 1-사상의 매끄러운 다양체는
 이다.
이다.
- 1-사상
 ,
,  의 합성은
의 합성은  이다.
이다.
이에 대응하는 리 준대수는  위의 벡터장들의 리 준대수
위의 벡터장들의 리 준대수  이다.
이다.
참고 문헌[편집]
외부 링크[편집]













































