영률
| 영률 | |
|---|---|
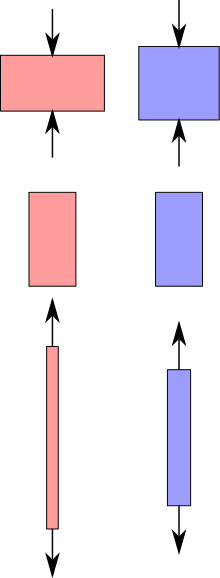 주어진 단축 응력 하에서, 각각 장력, 압력이 가해질 때 강성이 낮은 붉은 재료가 강성이 높은 푸른 재료보다 더 많이 변형된다. 영률은 강성의 단위이다. | |
기호 | E, Y |
| SI 단위 | 파스칼 |
| SI 단위 표현 | Pa = kg m−1 s−2 |
다른 상태량에서의 유도식 | |
| 차원 | M L−1 T−2 |
영률(영어: Young’s modulus, Young modulus)은 고체 재료의 강성을 측정하는 역학적 특성이다. 영률은 단축(uniaxial) 변형 영역에서 선형 탄성 재료의 응력(단위 면적 당 힘)과 변형률 사이의 관계를 정의하는 탄성계수이다. 1차원의 예로 설명하면, 영률을 E라고 할 때, 변형력(stress) = E × 변형도(strain) 로 표현할 수 있다. 영률은 물체에 주어진 압력을 알 때 그 물체가 변형된 정도를 예측하는데에 쓰이고 반대로도 쓰인다.
영률을 이용하기 전에는 변형을 확인하기 위해서 훅 법칙 F=kx 을 적용하였다. 여기서 변형의 정도를 나타나는 것은 x, 물체에 주어진 힘은 F였고 상수 k는 물체의 모양과 구성물질을 함께 고려해야 하는 수였다. 물체의 변형과 힘의 관계식인 F = kx에 사용되는 상수 k를 알기 위해서는 새로운 물체마다 물리적인 시험이 필요했다. 하지만 영률은 모양을 고려하지 않아도 물질의 종류만 알고 있으면 알 수 있었기 때문에 공학 발전에 혁명적인 도움이 될 수 있었다.
영률은 19세기 영국의 과학자 토마스 영의 이름을 따 명명되었다. 하지만 개념 자체는 1727년에 레온하르트 오일러가 만들어냈고, 오늘날의 형태로 영률의 개념을 검증한 최초의 실험은 영이 영률 개념을 정립하기 25년 전, 1782년에 조르다노 리카티(en:Giordano Riccati)가 실시하였다.[1] 용어 modulus는 측정(measure)을 의미하는 라틴어 용어 modus의 지소사이다.
정의[편집]
선형 탄성[편집]
고형 재료는 압력이나 장력의 형태로 작은 하중이 작용할 때 탄성 변형을 겪을 것이다. 탄성 변형은 가역성이 있어서 재료에서 하중이 제거되면 원래의 형태로 되돌아온다.
응력과 변형이 0에 가까울 때는 응력 변형 곡선은 선형이고, 응력과 변형 사이의 관계는 응력이 변형에 비례한다는 훅 법칙으로 설명된다. 비례성의 상수는 영률이다. 영률이 클수록 같은 양의 변형을 일으키기 위해 더 많은 응력이 필요하다. 이상적인 강체는 무한대의 영률 값을 갖는다.
응력 변형 곡선이 선형인 것은 그리 많지 않으며 어느 정도 이상 변형이 일어나면 소성을 띄게 된다.
공식과 단위[편집]
- 는 영률이다.
- 는 단축 응력(uniaxial stress), 즉 단위 표면 당 단축 힘(uniaxial force)이다.
- 는 변형률, 즉 길이의 변화를 원래의 길이로 나눈 것이며 무차원의 값을 가진다.
와 은 압력의 단위를 가지는 반면, 은 무차원의 값을 가진다(단위 없음). 따라서 영률의 단위는 압력의 단위이므로 표준 단위도 파스칼과 같은 압력의 단위를 사용한다. 영률은 보통 파스칼로 표기하기에는 값이 너무 크기 때문에 메가파스칼(MPa 또는 N/mm2)이나 기가파스칼(GPa 또는 kN/mm2)로 표기한다.
혼동하기 쉬운 개념들[편집]
재료의 강성은 후술할 특성들과 혼동하지 말아야 한다:
- 강도: 재료가 탄성 변형 영역에 머물러있을 수 있는, 즉 영구적인 변형 없이 견딜 수 있는 최대 응력이다.
- 기하학적 강성: 재료의 국부적인 특성 뿐만 아니라 물체의 형태에 따라 달라지는 보편적인 물체의 특성이다. 예를 들면 I형강(en:I beam)은 같은 물질, 질량으로 만든 막대기보다 길이당 더 높은 휨 강성을 띈다;
- 경도(en:Hardness): 더 단단한 물체의 관통 대한 재료의 표면의 상대적인 저항성이다;
- 인성(en:Toughness): 균열이 일어나기 직전까지 물질이 흡수할 수 있는 에너지의 양이다.
활용[편집]
영률을 활용하면 인장이나 압축 하중이 가해진, 탄성 재료로 만들어진 봉의 치수의 변화를 계산할 수 있다. 예를 들면 재료 샘플이 인장 하중이 가해질 때 얼마나 늘어날지, 압축 하중이 가해질 때 얼마나 줄어들지 예측할 수 있다. 영률은 단축 응력, 즉 한 쪽 방향으로 인장 혹은 압축 응력이 가해지고 다른 방향으로는 아무 응력도 없을 경우에 바로 적용할 수 있다. 영률은 형강의 지지점 사이의 한 지점에 하중이 가해질 때 정정한 형강이 얼마나 휠지 예측하는 데도 활용할 수 있다. 여타의 탄성 계산은 보통 전단 탄성 계수, 체적 탄성 계수, 푸아송 비 등의 탄성 특성을 하나 더 필요로 한다. 이 변수 중 두 개만 있으면 등방성 재료의 탄성을 완전히 설명할 수 있다.
선형 대 비선형[편집]
영률은 훅 법칙에서 비례성의 요소를 나타내는데, 이는 응력과 변형률과 관계 있다. 하지만 훅 법칙은 재료가 '선형', '탄성'을 띈 상태에서만 유효하다. 현실에서는 어떠한 물질이라도 아주 큰 길이로 늘려지거나 굉장히 큰 힘을 가하면 결국 파괴될 것이다. 하지만 모든 고형 재료는 변형이나 응력이 충분히 크지 않을 경우 거의 훅 법칙을 따르는 반응을 보인다. 훅 법칙이 유효한 범위가 재료에 가해질 것으로 예상되는 응력을 감당하기에 충분히 큰 경우 재료가 선형성을 띈다(linear)고 하며, 그렇지 않은(일상적으로 가해지는 응력이 선형 범위를 넘어선) 경우 재료가 비선형성을 띈다(nonlinear)고 한다.
보통 강철, 탄소 섬유, 유리는 선형 재료로 여겨지며 고무, 토양 따위는 비선형 재료로 여겨진다. 하지만 이는 절대적인 분류가 아니다. 만일 비선형 재료에 굉장히 미미한 응력이나 변형이 가해진다면 그 반응은 선형적일 것이고, 선형 재료에 굉장히 큰 응력이나 변형이 가해질 때 나타나는 현상은 선형 이론으로는 설명하기 어려울 것이다. 예를 들면 선형 이론은 가역성을 가정하기 때문에, 강철 다리가 감당할 수 없을 정도로 높은 하중이 가해졌을 때 일어날 파괴를 묘사할 수는 없다. 강철이 대부분의 상황에서 선형 재료이기는 하지만, 그러한 끔찍한 파괴가 일어날 때에는 그렇지 않다.
고체 역학에서는 응력-변형도 선도의 임의의 기울기는 접선 계수(en:tangent modulus)라고 불린다. 접선 계수는 재료의 샘플을 활용해 수행하는 인장 시험을 통해 구하는 응력 변형도 선도의 기울기에서 실험적으로 결정할 수 있다.
방향성 재료(Directional materials)[편집]
영률은 언제나 모든 방향에서 같지는 않다. 대부분의 금속과 세라믹, 그리고 수많은 여타의 물질들은 등방성이며, 그 역학적 성질은 모든 방향에서 같다. 하지만 금속과 세라믹은 특정한 불순물을 함유할 수 있으며, 금속은 그 결정 구조가 방향성을 띄도록 기계적으로 가공할 수 있다. 그렇게 되면 이 물질들은 비등방성을 띄며, 영률은 힘 벡터의 방향에 따라 달라지게 된다. 비등방성은 다양한 합성재료에서 찾아볼 수 있다. 예를 들면 탄소섬유는 (입자 사이의) 섬유에 평행한 방향으로 힘이 가해질 때 영률이 훨씬 높다. 이 밖에도 목재, 강화 콘크리트 따위가 비등방성을 띈다. 공학자들은 이러한 방향성을 구조물을 지을 때 적절하게 활용할 수 있다.
계산[편집]
영률 E는 물리적인 응력-변형도 선도의 탄성 (초반, 선형) 구간에서 인장 응력 을 공칭 변형률 로 나눠서 계산할 수 있다:
- E는 영률(탄성 계수)이다;
- F는 물체에 장력이 가해질 때 생겨나는 힘이다;
- A는 실제의 단면적인데, 작용된 힘의 방향에 수직하는 단면의 면적과 동일하다;
- ΔL 은 물체의 길이가 변한 양이다(ΔL 은 금속이 늘어나면 양수이고 압축되면 음수이다);
- L0 은 물체의 원래 길이다.
인장 혹은 압축된 재료로 인한 힘[편집]
어떤 재료의 영률은 특정한 변형률 하에서 재료가 가하는 힘을 계산할 때 사용될 수 있다.
F는 만큼 만큼 인장되거나 압축될 때 재료에서 가해진다.
이 공식에서 인장된 와이어를 위한 훅 법칙을 유도할 수 있다:
포화 상태일 때는 다음과 같다.
- and
하지만 코일 스프링의 탄성은 영률이 아니라 전단 탄성 계수를 통해 구한다는 것을 명심하자.
탄성 위치 에너지[편집]
선형 탄성 재료에 쌓인 탄성 위치 에너지(en:elastic potential energy)는 훅 법칙의 적분을 통해 구할 수 있다:
이제 다양한 변수를 활용해보자:
이는 (예를 들면 단위 부피 당) 탄성 위치 에너지 밀도는 다음과 같이 주어짐을 의미한다:
혹은 단순히 표기하자면, 선형 탄성 재료의 경우 인데, 변형률은 의 형태로 정의되기 때문이다.
비선형 탄성 재료에서 영률은 변형률에 관한 함수이므로 the second equivalence은 더 이상 성립되지 않고(the second equivalence no longer holds) 탄성 에너지는 변형률의 이차함수가 아니다:
탄성 상수 간의 관계[편집]
균질한 등방성 금속의 경우 탄성 상수(영률 E, 전단 탄성 계수 G, 부피 탄성 계수 K, 푸아송비 ν) 사이에는 단순한 관계가 성립하여 그 중 두 개의 값만 알고 있으면 나머지를 전부 계산할 수 있다:
온도 의존성[편집]
금속의 영률은 온도에 따라 달라지며, 원자 사이의 결합의 변화를 통해 실현되고, 따라서 이러한 변화는 금속의 일함수의 변화에 따라 달라진다는 것이 밝혀졌다. 고전적으로는 이러한 변화는 실증적 방식을 통해(this change is predicted through fitting), 명확한 기저의 기제(예를 들면 Watchman's formula) 없이 예측되었지만, Rahemi-Li model[3]은 어떻게 전자 일함수의 변화가 금속의 영률의 변화를 야기하는지 증명했으며 고체에 대한 레너드-존스 퍼텐셜(en:Lennard-Jones potential)의 일반화를 사용하여 계산 가능한 매개변수를 가지고 이러한 변화를 예견할 수 있다.
근삿값[편집]

영률은 샘플의 구성상태, 실험방법에 따라 조금씩 달라질 수 있다. 변형의 정도는 수집되는 데이터에 큰 영향을 끼칠 수 있는데, 특히 중합체의 경우가 심하다. 하단의 표에 제시된 값은 근삿값이며 단지 상대적 비교를 위한 수단일 뿐이다.
| 재료 | GPa | Mpsi |
|---|---|---|
| 고무 (낮은 변형율) | 0.01–0.1[4] | 1.45–14.5×10−3 |
| 저밀도 폴리에틸렌[5] | 0.11–0.86 | 1.6–6.5×10−2 |
| 규조류 규조각(en:frustule) (주로 규산)[6] | 0.35–2.77 | 0.05–0.4 |
| PTFE (테플론) | 0.5[4] | 0.075 |
| HDPE | 0.8 | 0.116 |
| 박테리오파지 캡시드[7] | 1–3 | 0.15–0.435 |
| 폴리프로필렌 | 1.5–2[4] | 0.22–0.29 |
| 폴리카보네이트 | 2–2.4 | 0.29-0.36 |
| 폴리에틸렌 테레프탈레이트 (PET) | 2–2.7[4] | 0.29–0.39 |
| 나일론 | 2–4 | 0.29–0.58 |
| 폴리스티렌, 고형 | 3–3.5[4] | 0.44–0.51 |
| 폴리스티렌, 거품[8] | 0.0025–0.007 | 0.00036–0.00102 |
| 중밀도 섬유판 (MDF)[9] | 4 | 0.58 |
| 나무 (along grain) | 11[4] | 1.60 |
| 인간 골피질[10] | 14 | 2.03 |
| 유리강화 폴리에스테르 망()[11] | 17.2 | 2.49 |
| 방향성(Aromatic) 펩타이드 나노관[12][13] | 19–27 | 2.76–3.92 |
| 고강도 콘크리트 | 30[4] | 4.35 |
| 아미노산 분자 결정 덩어리[14] | 21–44 | 3.04–6.38 |
| 탄소 섬유 강화 플라스틱 (50/50 fibre/matrix, biaxial fabric) | 30–50[15] | 4.35–7.25 |
| 삼 섬유[16] | 35 | 5.08 |
| 마그네슘 금속 (Mg) | 45[4] | 6.53 |
| 유리 | 50–90[4] | 7.25–13.1 |
| 아마 섬유[17] | 58 | 8.41 |
| 알루미늄 | 69[4] | 10 |
| 진주층(en:nacre), 주로 탄산칼슘[18] | 70 | 10.2 |
| 아라미드[19] | 70.5–112.4 | 10.2–16.3 |
| 법랑질, 주로 인산칼슘(en:calcium phosphate)[20] | 83 | 12 |
| 쐐기풀 섬유[21] | 87 | 12.6 |
| 청동 | 96–120[4] | 13.9–17.4 |
| 황동 | 100–125[4] | 14.5–18.1 |
| 티타늄 (Ti) | 110.3 | 16[4] |
| 티타늄 합금 | 105–120[4] | 15–17.5 |
| 구리 (Cu) | 117 | 17 |
| 탄소 섬유 강화 플라스틱 (70/30 fibre/matrix, unidirectional, along fibre)[22] | 181 | 26.3 |
| 다방향성(different directions) 실리콘 단결정[23][24] | 130–185 | 18.9–26.8 |
| 연철 | 190–210[4] | 27.6–30.5 |
| 강철 (ASTM-A36) | 200[4] | 29 |
| 다결정질 이트륨 철 석류석(en:Yttrium iron garnet) (YIG)[25] | 193 | 28 |
| 단결정 이트륨 철 석류석 (YIG)[26] | 200 | 29 |
| 코발트크롬(en:Cobalt-chrome)(CoCr)[27] | 220–258 | 29 |
| 방향성 펩타이드 나노구[28] | 230–275 | 33.4–40 |
| 베릴륨 (Be)[29] | 287 | 41.6 |
| 몰리브데넘 (Mo) | 329–330[4][30][31] | 47.7–47.9 |
| 텅스텐 (W) | 400–410[4] | 58–59 |
| 탄화규소(en:Silicon carbide) (SiC) | 450[4] | 65 |
| 탄화텅스텐 (WC) | 450–650[4] | 65–94 |
| 오스뮴 (Os) | 525–562[32] | 76.1–81.5 |
| 단일벽 탄소 나노튜브(en:Single-walled carbon nanotube) | 1,000+[33][34] | 150+ |
| 그래핀 (C) | 1050[35] | 152 |
| 다이아몬드 (C) | 1050–1210[36] | 152–175 |
| 카르빈(en:Linear acetylenic carbon) (C)[37] | 32100[38] | 4,660 |
참고 문서[편집]
- 휨강성(en:Bending stiffness)
- 휨
- 변형
- 휨계수(en:Flexural modulus)
- 훅 법칙
- 충격 여기 기법(en:Impulse excitation technique)
- 재료의 특성의 목록(en:List of materials properties)
- 항복( en:yield (engineering))
각주[편집]
- ↑ The Rational mechanics of Flexible or Elastic Bodies, 1638–1788: Introduction to Leonhardi Euleri Opera Omnia, vol. X and XI, Seriei Secundae. Orell Fussli.
- ↑ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). 온라인 수정 버전: (2006–) "modulus of elasticity (Young's modulus), E". doi 10.1351/goldbook.M03966
- ↑ Rahemi, Reza; Li, Dongyang (April 2015). “Variation in electron work function with temperature and its effect on the Young's modulus of metals”. 《Scripta Materialia》 99 (2015): 41–44. arXiv:1503.08250. doi:10.1016/j.scriptamat.2014.11.022.
- ↑ 가 나 다 라 마 바 사 아 자 차 카 타 파 하 거 너 더 러 머 버 “Elastic Properties and Young Modulus for some Materials”. The Engineering ToolBox. 2012년 1월 6일에 확인함.
- ↑ “Overview of materials for Low Density Polyethylene (LDPE), Molded”. Matweb. 2011년 1월 1일에 원본 문서에서 보존된 문서. 2013년 2월 7일에 확인함.
- ↑ Subhash G, Yao S, Bellinger B, Gretz MR (2005). “Investigation of mechanical properties of diatom frustules using nanoindentation”. 《J Nanosci Nanotechnol.》 5 (1): 50–6. doi:10.1166/jnn.2005.006. PMID 15762160.
- ↑ Ivanovska IL, de Pablo PJ, Sgalari G, MacKintosh FC, Carrascosa JL, Schmidt CF, Wuite GJ (2004). “Bacteriophage capsids: Tough nanoshells with complex elastic properties”. 《Proc Natl Acad Sci USA》 101 (20): 7600–5. Bibcode:2004PNAS..101.7600I. doi:10.1073/pnas.0308198101. PMC 419652. PMID 15133147.
- ↑ “Styrodur Technical Data” (PDF). BASF. 2016년 3월 15일에 확인함.
- ↑ “Medium Density Fiberboard (MDF) Material Properties :: MakeItFrom.com”. 2016년 2월 4일에 확인함.
- ↑ Rho, JY (1993). “Young's modulus of trabecular and cortical bone material: ultrasonic and microtensile measurements”. 《Journal of Biomechanics》 26 (2): 111–119. doi:10.1016/0021-9290(93)90042-d. PMID 8429054.
- ↑ "Polyester Matrix Composite reinforced by glass fibers (Fiberglass)". [SubsTech] (2008-05-17). Retrieved on 2011-03-30.
- ↑ Kol, N.; 외. (2005년 6월 8일). “Self-Assembled Peptide Nanotubes Are Uniquely Rigid Bioinspired Supramolecular Structures”. 《Nano Letters》 5 (7): 1343–1346. Bibcode:2005NanoL...5.1343K. doi:10.1021/nl0505896.
- ↑ Niu, L.; 외. (2007년 6월 6일). “Using the Bending Beam Model to Estimate the Elasticity of Diphenylalanine Nanotubes”. 《Langmuir》 23 (14): 7443–7446. doi:10.1021/la7010106. PMID 17550276.
- ↑ Azuri, I.; 외. (2015년 11월 9일). “Unusually Large Young's Moduli of Amino Acid Molecular Crystals”. 《Angew. Chem. Int. Ed.》 54 (46): 13566–13570. doi:10.1002/anie.201505813. PMID 26373817.
- ↑ “Composites Design and Manufacture (BEng) – MATS 324”. 2016년 11월 9일에 원본 문서에서 보존된 문서. 2019년 6월 6일에 확인함.
- ↑ Nabi Saheb, D.; Jog, JP. (1999). “Natural fibre polymer composites: a review”. 《Advances in Polymer Technology》 18 (4): 351–363. doi:10.1002/(SICI)1098-2329(199924)18:4<351::AID-ADV6>3.0.CO;2-X.
- ↑ Bodros, E. (2002). “Analysis of the flax fibres tensile behaviour and analysis of the tensile stiffness increase”. 《Composite Part A》 33 (7): 939–948. doi:10.1016/S1359-835X(02)00040-4.
- ↑ A. P. Jackson,J. F. V. Vincent and R. M. Turner (1988). “The Mechanical Design of Nacre”. 《Proceedings of the Royal Society B》 234 (1277): 415–440. Bibcode:1988RSPSB.234..415J. doi:10.1098/rspb.1988.0056.
- ↑ DuPont (2001). “Kevlar Technical Guide”: 9.
- ↑ M. Staines, W. H. Robinson and J. A. A. Hood (1981). “Spherical indentation of tooth enamel”. 《Journal of Materials Science》 16 (9): 2551–2556. Bibcode:1981JMatS..16.2551S. doi:10.1007/bf01113595.
- ↑ Bodros, E.; Baley, C. (2008년 5월 15일). “Study of the tensile properties of stinging nettle fibres (Urtica dioica)”. 《Materials Letters》 62 (14): 2143–2145. CiteSeerX 10.1.1.299.6908. doi:10.1016/j.matlet.2007.11.034.
- ↑ Epoxy Matrix Composite reinforced by 70% carbon fibers [SubsTech]. Substech.com (2006-11-06). Retrieved on 2011-03-30.
- ↑ "Physical properties of Silicon (Si)". Ioffe Institute Database. Retrieved on 2011-05-27.
- ↑ E.J. Boyd; 외. (February 2012). “Measurement of the Anisotropy of Young's Modulus in Single-Crystal Silicon”. 《Journal of Microelectromechanical Systems》 21 (1): 243–249. doi:10.1109/JMEMS.2011.2174415.
- ↑ Chou, H. M.; Case, E. D. (November 1988). “Characterization of some mechanical properties of polycrystalline yttrium iron garnet (YIG) by non-destructive methods”. 《Journal of Materials Science Letters》 7 (11): 1217–1220. doi:10.1007/BF00722341.
- ↑ “YIG properties” (PDF). 2003년 7월 20일에 원본 문서 (PDF)에서 보존된 문서. 2003년 7월 20일에 확인함.
- ↑ “Properties of cobalt-chrome alloys – Heraeus Kulzer cara”. 2015년 7월 1일에 원본 문서에서 보존된 문서. 2016년 2월 4일에 확인함.
- ↑ Adler-Abramovich, L.; 외. (2010년 12월 17일). “Self-Assembled Organic Nanostructures with Metallic-Like Stiffness”. 《Angewandte Chemie International Edition》 49 (51): 9939–9942. doi:10.1002/anie.201002037. PMID 20878815.
- ↑ Foley, James C.; 외. (2010). 〈An Overview of Current Research and Industrial Practices of Be Powder Metallurgy〉. Marquis, Fernand D.S. 《Powder Materials: Current Research and Industrial Practices III》. Hoboken, NJ, USA: John Wiley & Sons, Inc. 263쪽. doi:10.1002/9781118984239.ch32. ISBN 9781118984239.
- ↑ “Molybdenum: physical properties”. webelements. 2015년 1월 27일에 확인함.
- ↑ “Molybdenum, Mo” (PDF). Glemco. 2010년 9월 23일에 원본 문서 (PDF)에서 보존된 문서. 2014년 1월 27일에 확인함.
- ↑ D.K.Pandey; Singh, D.; Yadawa, P. K.; 외. (2009). “Ultrasonic Study of Osmium and Ruthenium” (PDF). 《Platinum Metals Rev.》 53 (4): 91–97. doi:10.1595/147106709X430927. 2020년 3월 12일에 원본 문서 (PDF)에서 보존된 문서. 2014년 11월 4일에 확인함.
- ↑ L. Forro; 외. “Electronic and mechanical properties of carbon nanotubes” (PDF). 2005년 10월 29일에 원본 문서 (PDF)에서 보존된 문서. 2019년 6월 6일에 확인함.
- ↑ Y. H. Yang; Li, W. Z.; 외. (2011). “Radial elasticity of single-walled carbon nanotube measured by atomic force microscopy”. 《Applied Physics Letters》 98 (4): 041901. Bibcode:2011ApPhL..98d1901Y. doi:10.1063/1.3546170.
- ↑ Fang Liu; Pingbing Ming & Ju Li. “Ab initio calculation of ideal strength and phonon instability of graphene under tension” (PDF).
- ↑ Spear and Dismukes (1994). 《Synthetic Diamond – Emerging CVD Science and Technology》. Wiley, N.Y. 315쪽. ISBN 978-0-471-53589-8.
- ↑ Owano, Nancy (2013년 8월 20일). “Carbyne is stronger than any known material”. 《phys.org》.
- ↑ Liu, Mingjie; Artyukhov, Vasilii I; Lee, Hoonkyung; Xu, Fangbo; Yakobson, Boris I (2013). “Carbyne From First Principles: Chain of C Atoms, a Nanorod or a Nanorope?”. 《ACS Nano》 7 (11): 10075–10082. arXiv:1308.2258. doi:10.1021/nn404177r. PMID 24093753.
참고 문헌[편집]
- ASTM E 111, "Standard Test Method for Young's Modulus, Tangent Modulus, and Chord Modulus"
- The ASM Handbook (various volumes) contains Young's Modulus for various materials and information on calculations. Online version (구독 필요)
외부 링크[편집]
- Matweb: free database of engineering properties for over 115,000 materials
- Young's Modulus for groups of materials, and their cost
| 참고 공식 | |||||||
|---|---|---|---|---|---|---|---|
| 균질한 등방성 선형 탄성 재료는 상술한 탄성 계수들 중 두 개로 고유하게 결정되는 탄성 특성을 갖는다. 따라서, 두 개의 탄성 계수만 알고 있으면 나머지는 후술할 공식들로 계산할 수 있다. | |||||||
| 비고 | |||||||
유효한 해는 두 개다. +은 을 유도한다. −은 을 유도한다. | |||||||
| 일 때는 사용할 수 없다. | |||||||














































































































