기하학 에서 사인 법칙 (-法則, 영어 : law of sines ) 혹은 라미의 정리 는 삼각형 의 변의 길이와 각의 사인 사이의 관계를 나타내는 정리이다. 이에 따라 삼각형의 두 각의 크기와 한 변의 길이를 알 때 남은 두 변의 길이를 구할 수 있다.
삼각형
A
B
C
{\displaystyle ABC}
A
,
B
,
C
{\displaystyle A,B,C}
a
,
b
,
c
{\displaystyle a,b,c}
사인 법칙 에 따르면 다음이 성립한다.[1] :20, 52
a
sin
A
=
b
sin
B
=
c
sin
C
=
2
R
{\displaystyle {\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}=2R}
여기서
R
{\displaystyle R}
A
B
C
{\displaystyle ABC}
외접원 의 반지름 이다.
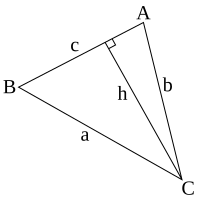
삼각형의 넓이를 통한 증명 [ 편집 ] 사인 법칙의 증명 삼각형
A
B
C
{\displaystyle ABC}
c
{\displaystyle c}
h
{\displaystyle h}
[1] :20
h
=
b
sin
A
{\displaystyle h=b\sin A}
A
B
C
{\displaystyle ABC}
K
{\displaystyle K}
K
=
1
2
c
h
=
1
2
b
c
sin
A
{\displaystyle K={\frac {1}{2}}ch={\frac {1}{2}}bc\sin A}
자모를 치환하면 다음과 같은 등식을 얻는다.
2
K
=
b
c
sin
A
=
a
c
sin
B
=
a
b
sin
C
{\displaystyle 2K=bc\sin A=ac\sin B=ab\sin C}
양변에
a
b
c
{\displaystyle abc}
sin
A
a
=
sin
B
b
=
sin
C
c
{\displaystyle {\frac {\sin A}{a}}={\frac {\sin B}{b}}={\frac {\sin C}{c}}}
외접원을 통한 증명 [ 편집 ]
C
{\displaystyle C}
가 예각일 경우
C
{\displaystyle C}
가 직각일 경우
C
{\displaystyle C}
가 둔각일 경우
삼각형
A
B
C
{\displaystyle ABC}
외접원 을 그리자.[1] :52
A
{\displaystyle A}
A
D
{\displaystyle AD}
A
B
D
{\displaystyle ABD}
A
D
=
2
R
{\displaystyle AD=2R}
c
=
2
R
sin
D
{\displaystyle c=2R\sin D}
만약
C
{\displaystyle C}
C
{\displaystyle C}
D
{\displaystyle D}
원주각 이므로
∠
C
=
∠
D
{\displaystyle \angle C=\angle D}
c
=
2
R
sin
C
{\displaystyle c=2R\sin C}
만약
C
{\displaystyle C}
B
{\displaystyle B}
D
{\displaystyle D}
2
R
=
c
{\displaystyle 2R=c}
sin
C
=
1
{\displaystyle \sin C=1}
C
{\displaystyle C}
C
{\displaystyle C}
D
{\displaystyle D}
내접 사각형 의 두 마주보는 각이므로,
∠
C
=
π
−
∠
D
{\displaystyle \angle C=\pi -\angle D}
A
,
B
{\displaystyle A,B}
코사인 법칙을 통한 증명 [ 편집 ] 코사인 법칙 에 따라 다음이 성립한다.[2] :180
sin
2
A
a
2
=
1
−
cos
2
A
a
2
=
4
b
2
c
2
−
4
b
2
c
2
cos
2
A
4
a
2
b
2
c
2
=
4
b
2
c
2
−
(
b
2
+
c
2
−
4
b
c
)
2
4
a
2
b
2
c
2
=
(
a
+
b
+
c
)
(
a
+
b
−
c
)
(
a
−
b
+
c
)
(
b
+
c
−
a
)
4
a
2
b
2
c
2
{\displaystyle {\begin{aligned}{\frac {\sin ^{2}A}{a^{2}}}&={\frac {1-\cos ^{2}A}{a^{2}}}\\&={\frac {4b^{2}c^{2}-4b^{2}c^{2}\cos ^{2}A}{4a^{2}b^{2}c^{2}}}\\&={\frac {4b^{2}c^{2}-(b^{2}+c^{2}-4bc)^{2}}{4a^{2}b^{2}c^{2}}}\\&={\frac {(a+b+c)(a+b-c)(a-b+c)(b+c-a)}{4a^{2}b^{2}c^{2}}}\end{aligned}}}
결과가
a
,
b
,
c
{\displaystyle a,b,c}
구면 사인 법칙 [ 편집 ] 단위 구면 위의 구면 삼각형
A
B
C
{\displaystyle ABC}
A
,
B
,
C
{\displaystyle A,B,C}
a
,
b
,
c
{\displaystyle a,b,c}
구면 사인 법칙 (球面-法則, 영어 : spherical law of sines )에 따르면 다음이 성립한다.
sin
a
sin
A
=
sin
b
sin
B
=
sin
c
sin
C
{\displaystyle {\frac {\sin a}{\sin A}}={\frac {\sin b}{\sin B}}={\frac {\sin c}{\sin C}}}
구면 사인 법칙의 증명 [ 편집 ] 순수 기하 증명 [ 편집 ] 구의 중심을
O
{\displaystyle O}
O
A
{\displaystyle OA}
P
{\displaystyle P}
P
{\displaystyle P}
B
O
C
{\displaystyle BOC}
P
D
{\displaystyle PD}
D
{\displaystyle D}
O
B
,
O
C
{\displaystyle OB,OC}
D
E
,
D
F
{\displaystyle DE,DF}
삼수선 정리 에 따라
P
E
,
P
F
{\displaystyle PE,PF}
O
B
,
O
C
{\displaystyle OB,OC}
P
D
=
P
E
sin
B
=
O
P
sin
c
sin
B
{\displaystyle PD=PE\sin B=OP\sin c\sin B}
P
D
=
P
F
sin
C
=
O
P
sin
b
sin
C
{\displaystyle PD=PF\sin C=OP\sin b\sin C}
두 식에서
P
D
/
O
P
{\displaystyle PD/OP}
sin
b
sin
B
=
sin
c
sin
C
{\displaystyle {\frac {\sin b}{\sin B}}={\frac {\sin c}{\sin C}}}
남은 한 등식 역시 같은 방법으로 증명하면 구면 사인 법칙을 얻는다.[3] :21, Art. 42
벡터를 통한 증명 [ 편집 ] 구의 중심과 세 꼭짓점
A
,
B
,
C
{\displaystyle A,B,C}
a
,
b
,
c
{\displaystyle \mathbf {a} ,\mathbf {b} ,\mathbf {c} }
삼중곱 의 정의에 따라 다음이 성립한다.
(
a
×
b
)
×
(
a
×
c
)
=
(
(
a
×
b
)
⋅
c
)
a
{\displaystyle (\mathbf {a} \times \mathbf {b} )\times (\mathbf {a} \times \mathbf {c} )=((\mathbf {a} \times \mathbf {b} )\cdot \mathbf {c} )\mathbf {a} }
(
b
×
a
)
×
(
b
×
c
)
=
(
(
b
×
a
)
⋅
c
)
b
{\displaystyle (\mathbf {b} \times \mathbf {a} )\times (\mathbf {b} \times \mathbf {c} )=((\mathbf {b} \times \mathbf {a} )\cdot \mathbf {c} )\mathbf {b} }
(
c
×
a
)
×
(
c
×
b
)
=
(
(
c
×
a
)
⋅
b
)
c
{\displaystyle (\mathbf {c} \times \mathbf {a} )\times (\mathbf {c} \times \mathbf {b} )=((\mathbf {c} \times \mathbf {a} )\cdot \mathbf {b} )\mathbf {c} }
따라서 다음이 성립한다.
|
(
a
×
b
)
×
(
a
×
c
)
|
=
|
(
b
×
a
)
×
(
b
×
c
)
|
=
|
(
c
×
a
)
×
(
c
×
b
)
|
{\displaystyle |(\mathbf {a} \times \mathbf {b} )\times (\mathbf {a} \times \mathbf {c} )|=|(\mathbf {b} \times \mathbf {a} )\times (\mathbf {b} \times \mathbf {c} )|=|(\mathbf {c} \times \mathbf {a} )\times (\mathbf {c} \times \mathbf {b} )|}
여기에 다음을 대입하면 구면 사인 법칙을 얻는다.
|
(
a
×
b
)
×
(
a
×
c
)
|
=
sin
c
sin
b
sin
A
{\displaystyle |(\mathbf {a} \times \mathbf {b} )\times (\mathbf {a} \times \mathbf {c} )|=\sin c\sin b\sin A}
|
(
b
×
a
)
×
(
b
×
c
)
|
=
sin
c
sin
a
sin
B
{\displaystyle |(\mathbf {b} \times \mathbf {a} )\times (\mathbf {b} \times \mathbf {c} )|=\sin c\sin a\sin B}
|
(
c
×
a
)
×
(
c
×
b
)
|
=
sin
b
sin
a
sin
C
{\displaystyle |(\mathbf {c} \times \mathbf {a} )\times (\mathbf {c} \times \mathbf {b} )|=\sin b\sin a\sin C}
구면 코사인 법칙을 통한 증명 [ 편집 ] 제1 구면 코사인 법칙 을 사용하여 구면 사인 법칙을 다음과 같이 증명할 수 있다.[3] :20-21, Art. 40, 41
sin
2
A
sin
2
a
=
1
−
cos
2
A
sin
2
a
=
sin
2
b
sin
2
c
−
sin
2
b
sin
2
c
cos
2
A
sin
2
a
sin
2
b
sin
2
c
=
sin
2
b
sin
2
c
−
(
cos
a
−
cos
b
cos
c
)
2
sin
2
a
sin
2
b
sin
2
c
=
1
−
cos
2
a
−
cos
2
b
−
cos
2
c
+
2
cos
a
cos
b
cos
c
sin
2
a
sin
2
b
sin
2
c
{\displaystyle {\begin{aligned}{\frac {\sin ^{2}A}{\sin ^{2}a}}&={\frac {1-\cos ^{2}A}{\sin ^{2}a}}\\&={\frac {\sin ^{2}b\sin ^{2}c-\sin ^{2}b\sin ^{2}c\cos ^{2}A}{\sin ^{2}a\sin ^{2}b\sin ^{2}c}}\\&={\frac {\sin ^{2}b\sin ^{2}c-(\cos a-\cos b\cos c)^{2}}{\sin ^{2}a\sin ^{2}b\sin ^{2}c}}\\&={\frac {1-\cos ^{2}a-\cos ^{2}b-\cos ^{2}c+2\cos a\cos b\cos c}{\sin ^{2}a\sin ^{2}b\sin ^{2}c}}\end{aligned}}}
쌍곡 사인 법칙 [ 편집 ] 가우스 곡률 이 -1인 쌍곡면 위의 쌍곡 삼각형
A
B
C
{\displaystyle ABC}
A
,
B
,
C
{\displaystyle A,B,C}
a
,
b
,
c
{\displaystyle a,b,c}
쌍곡 사인 법칙 (雙曲-法則, 영어 : hyperbolic law of sines )에 따르면 다음이 성립한다.[4] :72
sinh
a
sin
A
=
sinh
b
sin
B
=
sinh
c
sin
C
{\displaystyle {\frac {\sinh a}{\sin A}}={\frac {\sinh b}{\sin B}}={\frac {\sinh c}{\sin C}}}
여기서
sinh
{\displaystyle \sinh }
쌍곡 사인 이다.
쌍곡 사인 법칙의 증명 [ 편집 ] 쌍곡 코사인 법칙을 통한 증명 [ 편집 ] 제1 쌍곡 코사인 법칙 을 사용하여 쌍곡 사인 법칙을 다음과 같이 증명할 수 있다.[4] :74
sin
2
A
sinh
2
a
=
1
−
cos
2
A
sinh
2
a
=
sinh
2
b
sinh
2
c
−
sinh
2
b
sinh
2
c
cos
2
A
sinh
2
a
sinh
2
b
sinh
2
c
=
sinh
2
b
sinh
2
c
−
(
cosh
b
cosh
c
−
cosh
a
)
2
sinh
2
a
sinh
2
b
sinh
2
c
=
1
−
cosh
2
a
−
cosh
2
b
−
cosh
2
c
+
2
cosh
a
cosh
b
cosh
c
sinh
2
a
sinh
2
b
sinh
2
c
{\displaystyle {\begin{aligned}{\frac {\sin ^{2}A}{\sinh ^{2}a}}&={\frac {1-\cos ^{2}A}{\sinh ^{2}a}}\\&={\frac {\sinh ^{2}b\sinh ^{2}c-\sinh ^{2}b\sinh ^{2}c\cos ^{2}A}{\sinh ^{2}a\sinh ^{2}b\sinh ^{2}c}}\\&={\frac {\sinh ^{2}b\sinh ^{2}c-(\cosh b\cosh c-\cosh a)^{2}}{\sinh ^{2}a\sinh ^{2}b\sinh ^{2}c}}\\&={\frac {1-\cosh ^{2}a-\cosh ^{2}b-\cosh ^{2}c+2\cosh a\cosh b\cosh c}{\sinh ^{2}a\sinh ^{2}b\sinh ^{2}c}}\end{aligned}}}
같이 보기 [ 편집 ] 외부 링크 [ 편집 ]