병렬 컴퓨팅

병렬 컴퓨팅(parallel computing) 또는 병렬 연산은 동시에 많은 계산을 하는 연산의 한 방법이다. 크고 복잡한 문제를 작게 나눠 동시에 병렬적으로 해결하는 데에 주로 사용되며,[1] 병렬 컴퓨팅에는 여러 방법과 종류가 존재한다. 그 예로, 비트 수준, 명령어 수준, 데이터, 작업 병렬 처리 방식 등이 있다. 병렬 컴퓨팅은 오래전부터 주로 고성능 연산에 이용되어 왔으며, 프로세서 주파수[2]의 물리적인 한계에 다가가면서 문제 의식이 높아진 이후에 더욱 주목받게 되었다. 최근 컴퓨터 이용에서 발열과 전력 소모에 대한 관심이 높아지는 것과 더불어 멀티 코어 프로세서를 핵심으로 컴퓨터 구조에서 강력한 패러다임으로 주목받게 되었다.[3]
병렬 컴퓨터들은 대체적으로 하드웨어의 병렬화 방법에 따라 분류된다. 클러스터, MPP, 그리드는 여러 컴퓨터에서 한 가지 작업을 하도록 설계되었다. 멀티 코어나 멀티 프로세서 컴퓨터들은 여러 개의 처리 요소(CPU 등)을 한 기기에 탑재하고 작업한다. 특수화된 병렬 컴퓨터 구조들은 가끔씩 고전적인 프로세서들과 함께 특정한 작업을 가속화 시키는 목적으로도 사용된다.
병렬 컴퓨터 프로그램들은 순차적 프로그램보다 난해하다.[4] 왜냐하면 동시처리는 여러 종류의 새로운 잠재적 소프트웨어 버그를 가지고 있기 때문이다. (경쟁 상태가 가장 흔하다) 통신과 동기화를 요구하는 다른 하위 작업들은 병렬 프로그램 성능의 전형적인 방해요소다. 병렬화된 프로그램의 속도 향상은 암달의 법칙에 의해서 그 결과가 결정된다.
배경[편집]
전통적으로 컴퓨터 소프트웨어는 직렬 컴퓨팅 방식을 기본으로 작성되어 왔다. 문제를 해결하는 데 있어서 알고리즘은 직렬형 명령들로 이루어졌고 그 명령들은 하나의 CPU에 의해서 실행되었다. 한 명령이 한 번에 하나씩 실행된다. 하나가 끝나면 그 다음 명령이 실행된다.[5]
병렬 컴퓨팅은 여러 개의 처리 요소(프로세서 등)를 이용하여 한 번에 문제를 해결한다. 이것은 그 문제를 독립적인 부분들로 나눠서 각 처리 요소가 그 부분의 알고리즘들을 한 번에 다른 요소들과 처리를 할 수 있게 하는 것을 가능하게 했다. 그 처리요소들은 여러 자원들을 포함한다. 예를 들면 한 컴퓨터에 있는 멀티프로세서, 여러 네트워크 컴퓨터들, 특수 하드웨어, 아니면 그런 것들을 섞어 쓸 수도 있다.[5]
컴퓨터의 클럭 속도는 1980년도 중반부터 2004년까지 컴퓨터 성능을 향상시키는 데 가장 영향력 있는 요소였다. 프로그램 실행시간은 명령어 수를 명령어 당 평균시간을 곱한 것과 같았는데 클럭수를 늘리면 명령을 실행하는 평균시간은 짧아진다.
그러나 칩의 전력소모량은P = C × V2 × F의 공식에 따른다. 여기서, P는 전력, C는 한 클럭 주기 당 스위칭된 전기용량(입력이 변화하는 트랜지스터의 개수에 비례), V는 전압(voltage)이고 F는 주파수(프로세서 속도)를 의미한다.[6] 주파수 수(프로세서 속도)를 높이면 전력 사용량이 늘어난다는 뜻이다. 전력 사용량이 계속 높아가자 결국 인텔은 2004년 5월에 테자스와 제이호크(Tejas and Jayhawk)를 취소시키기에 이른다. 그 사건은 주파수 척도에 의한 컴퓨터 구조 패러다임이 끝나는 것을 의미하게 된다.[7]
무어의 법칙은 매 18에서 24개월 동안 집적도가 두 배씩 늘어난다는 것을 예측하는데,[8] 전력소모량 사건에 계속됐던 예측은 끝이나고 말지만 무어의 법칙은 여전히 유효하다. 주파수 척도는 끝이 났지만 추가적인 트랜지스터들은 추가적인 병렬 컴퓨팅에 쓰이게 된다.
암달의 법칙과 구스타프슨의 법칙[편집]
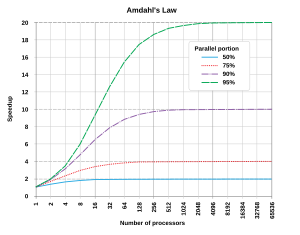
병렬화로 인한 속도 향상중 제일 좋은 것은 역시 선형적 결과다. 프로세서 수를 두 배로 늘리면 두 배 역할을 해서 실행시간을 절반으로 줄이고 프로세서 수를 또 두 배로 늘리면 또 실행시간이 절반으로 줄어든다. 그런데 아주 적은수의 병렬 알고리즘만이 최적의 속도 향상을 달성했다. 대부분은 그저 비슷한 선형적 속도 향상을 적은 수의 처리요소(프로세서)로 달성했을 뿐이다. 그것들은 처리 요소들의 숫자가 많아질수록 효과가 적어진다.
병렬 컴퓨팅 기반에서 잠재적인 속도 향상 알고리즘인 암달의 법칙은 1960년대에 진 암달에 의해서 만들어졌다.[9] 병렬화할 수 없는 작은 부분의 프로그램은 전체적인 병렬화에 영향(제한)을 가져온다는 것이었다. 수학적이나 공학적 문제들은 전통적으로 몇 가지 병렬화된 부분과 병렬화되지 않은 부분으로 구성되게 된다. 이 관계는 아래와 같은 공식으로 나타나게 된다.
여기서 S는 프로그램의 속도 향상을, P는 병렬화 가능한 분수를 의미한다. 만약 프로그램의 10%가 순차적 부분이라면 우리는 몇 개의 프로세서를 추가하든 간에 10배 이상 속도를 높일 수가 없다. 이것이 실용적으로 병렬실행 유닛들을 추가할 수 있는 한계이다. 순차적 부분의 제한으로 작업을 더 이상 나눌 수 없게 될 때 응용 프로그램들은 그 이상 빠른 결과를 만들 수 없게 된다. 인월미신의 예를 인용하자면 “임산부가 아무리 많아도 아이를 낳는 데에는 9개월이 걸린다.”
구스타프슨의 법칙은 컴퓨터 공학의 또 다른 법칙인데, 암달의 법칙과는 밀접한 관계가 있다. 이 공식은 다음과 같다:
P는 프로세서 수고 S는 속도 향상. α는 비 병렬 부분이다.[10] 암달의 법칙은 문제가 고정된 크기라는 것과 순차적 부분을 독립적인 프로세서들이라고 가정한다. 구스타프슨의 법칙은 그런 가정을 하지 않는다.
종속성[편집]
병렬 알고리즘은 자료 종속성을 이해하는 것이 기본이 된다. 어떤 프로그램도 가장 길게 연결되어 있는 종속적(비독립) 계산보다 빠르게 실행될 수 없다. (크리티컬 패스라고도 함) 이는 계산들이 이전 계산에 종속되어 있으면 계산은 그 차례를 지켜야 한다는 것을 뜻한다. 그러나 대부분 알고리즘들은 그런 긴 종속의 연결을 포함하지 않는다. 일반적인 병렬에서는 비종속적인(독립적인) 계산을 실행할 가능성이 많다.
Pi 와 Pj 두 프로그램 조각들이 있다고 하자. 번스타인 상태[11]는 두 개의 독립적이고 병렬적으로 실행될 수 있을 때를 설명한다. Ii는 Pi의 입력 변수고 Oi는 출력 변수라고 하고 Pj 도 같이 그렇다고 하자. 만약 다음을 만족시키면 Pi와 Pj는 독립적이다.
첫 번째 상태의 위반은 종속성 흐름(flow dependency) 을 야기한다. 첫 번째 문(文)을 일치시키는 것은 두 번째 문이 작성한 결과를 만든다. 두 번째 상태는 대 종속성(anti-dependency) 상태를 의미한다. 첫 번째 문이 두 번째 문에 의해 필요가 된 변수를 덮어쓸 때 세 번째와 마지막 상태는 출력의 독립을 의미하게 된다. 두 개의 문들이 같은 장소에서 작성할 때 마지막 결과는 논리적으로 반드시 마지막으로 실행됐던 명령이 되어야 한다.[12]
아래 함수는 몇가지 종속성을 보여준다.
function Dep(a, b)
c := a*b
d := 2*c
end function
Dep 함수 세 번째 줄은 두 번째 줄이 실행되기 전에는 실행될 수 없다. 왜냐하면 세 번째 줄은 두 번째줄의 결과에 의해서 실행되어야 하기 때문이다. 이것은 첫 번째 상태를 위반한 것이다. 즉, 종속성 흐름을 야기시킨다.
function NoDep(a, b)
c := a*b
d := 2*b
e := a+b
end function
이 예에서 명령어 간에 종속성은 없다, 따라서 이것들은 병렬로 처리할 수 있다.
번스타인의 상태는 다른 프로세스들 간에 메모리 공유를 허용하지 않는다. 그 때문에 서로 접근할 수 있게 만드는 방법이 필요할지도 모른다. 예를 들면 세마포어나 배리어나 아니면 다른 동기화 방법들 말이다.
경쟁상태, 상호배제, 동조화, 병렬감속[편집]
병렬 프로그램에서 하위 작업들은 스레드라고 불리기도 한다. 몇몇 병렬 컴퓨터 구조는 작고 경량화된 버전의 스레드인 파이버를 이용하기도 하고 큰 버전으로는 프로세스 라고도 한다. 그러나 “스레드”는 일반적으로 하위 작업을 가리키는 단어로 해석된다. 스레드들은 자기들끼리 공유되는 몇몇 변수들을 갱신할 필요가 있다. 두 프로그램들 사이의 명령어들은 아마 끼워넣을 지도 모른다. 예를 들자면 아래 프로그램을 보자.
| 스레드 A | 스레드 B |
| 1A: 변수 V를 읽는다 | 1B: 변수 V를 읽는다 |
| 2A: 변수 V에 1 을 추가한다 | 2B: 변수 V에 1 을 추가한다 |
| 3A: 변수 V를 써넣는다 | 3B: 변수 V를 써넣는다 |
만약 명령어 1B가 1A과 3A 사이에서 실행되었다거나 1A가 1B나 3B 사이에서 실행되었다면 프로그램은 잘못된 정보를 만들게 된다. 이것을 바로 “경쟁 상태” 라고 한다. 프로그래머는 반드시 락을 사용해서 상호 배제를 해야 한다. 락은 한 개의 스레드가 락이 풀리기 전까지 변수를 제어하고 다른 스레드가 읽거나 쓰는 것을 막는 프로그래밍 언어 구조체다. 스레드는 락을 임계 구역 (몇몇 변수를 접근할 수 있게 허용해 주는 프로그램 구역) 내에서 자유롭게 실행할 수 있게 만든다. 그리고 다 끝나면 잠금을 해제한다. 따라서 올바른 프로그램 실행을 보장시켜준다. 위의 프로그램을 락을 사용해서 다시 작성하면 다음과 같다.
| 스레드 A | 스레드 B |
| 1A: 변수V를 잠금 | 1B: 변수V를 잠금 |
| 2A: 변수V를 읽음 | 2B: 변수V를 읽음 |
| 3A: 변수V에 1 추가 | 3B: 변수V에 1 추가 |
| 4A: 변수 V를 써넣는다 | 4B: 변수 V를 써넣는다 |
| 5A: 변수V를 잠금해제 | 5B: 변수V를 잠금해제 |
다른 스레드가 락 아웃( V가 다시 풀릴 때까지 진행하지 못하게 함)될 때 한 스레드는 변수V를 성공적으로 잠갔다. 이것은 프로그램이 정상적으로 실행되는 것을 보장한다. 잠금은 프로그램이 정상적으로 실행되는 것을 반드시 보장하지만 프로그램 속도를 느리게 할 수도 있다.
여러 개의 변수들을 비원자성을 사용해서 잠그면 교착 상태에 빠질 수도 있다. 원자성 락은 한꺼번에 여러 개의 변수를 잠근다. 만약 전부다 잠글수 없다면 아무것도 잠그지 않는다. 만약 두 개의 스레드들이 서로 같은 두 변수들을 비원자성을 사용해서 잠가야 한다면 한 개의 스레드는 하나를 잠글지도 모르고 그러면 두 번째 스레드는 두 번째 변수를 잠가야 한다. 이 경우 두 스레드 다 잠그지 않을것이다. 그리고 교착 상태로 이어진다.
많은 병렬 프로그램들이 하위작업으로 동기화를 필수로 한다. 배리어는 그 작업에 필요한데, 배리어는 원래 소프트웨어 락에 포함 (implement) 되어 사용된다. 한 클래스의 알고리즘들인 비차단 동기화 (lock-free와 wait-free 알고리즘)는 모두 락과 배리어의 사용을 피한다. 그러나 이 접근은 일반적으로 포함시키기 어렵고 정확한 디자인의 자료구조를 요구하게 된다.
모든 병렬화가 속도 향상을 시키진 않는다. 일반적으로 스레드들을 나누면 나눌수록 그 스레드들은 서로 의사소통 하는 데 시간을 더 증가시킨다. 결국 의사소통에 의한 문제를 해결하기 위해서 간접적인 시간소모를 해야하고 그 이상의 병렬화는(부하를 나누기 위해 스레드들을 나눌 때) 실행시간을 단축시키기는커녕 늘리게 된다. 이것을 병렬 감속이라고 한다.
잘게 나눔(fine-grained), 크게 나눔(coarse-grained), 처치 곤란 병렬(embarrassingly parallel)[편집]
응용 프로그램들은 가끔 얼마나 자주 하위 작업들이 동기화 되나 혹은 서로 통신해야 하냐에 따라서 분류가 나뉘기도 한다. 만약 병렬 응용 프로그램의 하위 작업들이 초당 통신을 많이 해야 하면 잘게 나뉘었다고 하고 초당 통신을 많이 안해도 되면 크게 나뉘었다고 한다. 그리고 만약 아주 가끔 통신하거나 아예 하지 않는다면 처치 곤란 병렬 이라고 한다. 처치 곤란 병렬 응용 프로그램은 가장 쉬운 병렬화로 알려져 있다.
일관성 모델들[편집]
병렬 프로그래밍 언어와 병렬 컴퓨터들은 반드시 일관성 모델 (메모리 모델이라고도 불린다) 을 가지고 있어야 한다. 일관성 모델이란 컴퓨터 메모리 위에서 어떻게 연산들을 할 것인지와 어떻게 결과들을 만들것인지 규칙을 정의하는 것이다.
일관성 모델 중에는 레슬리 램포트의 순차 일관성 모델 (sequential consistency)이라는 것이 있다. 순차 일관성이란 병렬 프로그램 실행시 순차적 프로그램에서 나오는 결과와 똑같이 만드는 병렬 프로그램의 특성이다. 특히 만약에 “…어떤 실행에서의 결과가 모든 프로세서들의 연산이 어떤 순차적인 차례로 실행되거나 그 연산들의 각 독립적인 프로세서가 그 프로그램에 의해 보여주는 순서가 똑같다면” 프로그램은 순차적으로 모순이 없다.
소프트웨어 트랜잭셔널 메모리 (Software transactional memory (이하 STM))는 흔한 방식의 일관성 모델이다. STM은 데이터베이스 이론에서 원자 트랜잭션의 컨셉과 그것을 메모리 접근에 적용한걸 가져온 것이다.
수학적으로 이런 모델들은 여러 가지 방법으로 표현될 수 있다. 1962년 칼 아담 페트리의 박사 논문으로 소 개된 페트리 넷은 일찍이 일관성 모델들을 체계적으로 분류하는걸 시도했던 사례다. 자료흐름 이론(dataflow theory) 은 그것을 기반으로 만들어졌고 자료흐름 구조 (Dataflow architectures)는 자료흐름 이론의 아이디어들을 물리적인 방법에 의해 만들어졌다. 1970년도 후반에 시작된 통신 시스템 미적분 (Calculus of Communicating System) 이나 소통 순차적 프로세스 (Communicating Sequential Processes)들 같은 프로세스 미적분 (process calculi)들이 구성요소들의 상호 통합이라는 대수적 논리에 의해서 개발될 수 있었다. 좀 더 최근에는 파이-미적분 같은 미적분 들이 동적 기하학에 대한 성능 향상을 위해 그 프로세스에 추가되었다. 램포트의 TLA+ 같은 논리들과 대각합 (traces)이나 액터 이벤트 다이어그램 (Actor event diagrams) 같은 수학적 모델들이 동시 행위 시스템의 행동을 설명하기 위해서 개발됐다.
플린의 분류학[편집]
마이클 J. 플린은 가장 쉬운 컴퓨터와 프로그램 병렬(과 순차) 분류 시스템 중에 하나를 만들었다. 이것은 플린의 분류학(영어: Flynn's taxonomy)이라고도 알려져 있다. 플린은 프로그램들과 컴퓨터들을 그것이 단일, 아니면 복수의 명령어 셋을 사용하느냐 아니냐 그리고 그 명령으로 단일 아니면 복수의 데이터 들을 연산하는지 여부에 따라서 분류를 했다.
| 단일 명령어 |
복수 명령어 | |
|---|---|---|
| 단일 자료 |
SISD | MISD |
| 복수 자료 |
SIMD | MIMD |
SISD(단일명령-단일자료)는 완전히 순차적 프로그램과 같다. SIMD(단일명령-복수자료)는 반복되는 큰 자료에 대한 연산을 한다. SIMD는 일반적으로 신호처리 응용 프로그램들에서 실행된다. MISD(복수명령-단일자료)는 거의 쓰이지 않는 분류인데, 컴퓨터 구조들이 이것을 고민하고 있을 때(시스톨릭 배열같은 것들) 몇몇 응용 프로그램들이 이 분류를 구현시켜냈다. MIMD(복수명령-복수자료) 프로그램들은 제일 흔한 종류의 병렬 프로그램들이다.
데이비드 A. 패터슨과 존 L. 헤네시에 따르면 “몇 머신들은 이 카테고리를 여러 개 가질수도 있다, 당연히, 그런데 이 오래된 모델은 살아남는다. 왜냐하면 간단하고 이해하기 쉽기도 하고 처음 배울 때 좋다. 그리고 또 아마 어떤 조직을 넓게 이해하는 데 가장 많이 쓰였기 때문이다.”[13]
병렬처리의 종류[편집]
비트수준 병렬처리[편집]
초고밀도 집적회로(VLSI)의 등장으로 1970년대부터 1986년까지 컴퓨터 칩 제조 기술은 두 배의 워드 크기를 가진 컴퓨터 구조를 만들어 내서 속도 향상을 달성했다. 프로세서의 정보량은 사이클 단위의 조작이 가능했는데[14], 워드 크기를 늘리게 되면 워드 길이보다 큰 변수 위에서 실행되어야 했던 명령어 개수가 줄어들게 됐다. 예를 들자면, 8비트 프로세서는 반드시 16비트 정수형 두 개를 추가시켜야 한다. 프로세서는 반드시 먼저 8 하위 비트를 각 표준 추가 명령어를 정수형으로부터 추가시켜야 하고 그 다음에 하위에서 추가로 ADC 명령과 캐리를 사용하는 8 상위 비트를 추가시킨다. 8비트 프로세서는 한 개의 연산을 완료하기 위해서 2개의 명령어들을 필요로 하게 되고, 16비트 프로세서는 1개의 연산을 1개의 명령어로 끝낼수 있게 된다.
역사적으로 4비트 마이크로 프로세서들은 8비트, 16비트 그리고 32비트 마이크로 프로세서들에 의해서 교체됐다. 이 유행은 일반적으로 두 세대를 범용 컴퓨터 표준이 된32비트 프로세서의 등장과 함께 끝나는데, 최근 (2003-2004)엔 64비트 프로세서들을 가진x86-64 구조들이 등장하면서 표준이 된다.
명령어 수준 병렬 처리[편집]
컴퓨터 프로그램은 명령어들의 흐름이 프로세서에 의해서 실행되는걸 바탕으로 한다. 이 명령어들은 재 순차와 결과의 변경 없이 한꺼번에 그룹단위로 병렬실행이 가능했다. 이것을 명령어 수준 병렬화라고도 한다. 이 명령어 수준 병렬화는 80년대 중반부터 90년대 중반까지 컴퓨터 구조를 주름잡았다.[15]
현대의 프로세서들은 다단계 명령어 파이프라인을 가졌다. 파이프라인에서 각 단계는 다른 행동을 하는 같은 단계의 명령어를 실행하는 프로세서와 일치시킨다. N 스테이지 파이프라인은 N 개 만큼의 다른 명령어들을 다른 완료된 단계에서 가질수 있다. 파이프라인된 프로세서의 정석은 RISC 프로세서다. (다섯 개의 단계 – 명령어 패치, 디코드, 실행, 메모리 접근, 다시 써넣기 (write back) 가 정석이다.) 펜티엄 4 프로세서는 31단계의 파이프라인을 가지고 있다.[16]
파이프라인을 할 때 명령어 수준 병렬화에서 몇 프로세서들은 한 개 이상의 명령어를 한 번에 만들수 있었다. 이것을 슈퍼스칼라 프로세서라고도 한다. 만약에 자료종속성만 없다면 명령어들은 한꺼번에 합쳐질수 있다. 스코어보딩 (Scoreboarding)과 토마줄로 알고리즘 (스코어보딩과 비슷하지만 레지스터 리네이밍 (Register renaming)을 사용한다) 이 두 가지가 가장 흔한 비 순차적 실행과 명령어 수준 병렬화 기술들이다.
자료 병렬 처리[편집]
자료 병렬화는 프로그램 루프에 내재된 병렬화다. 프로그램 루프는 병렬로 처리된 다른 컴퓨팅 노드들의 자료를 분산시키는데 초점을 맞춘다. “루프를 병렬시키는 것은 가끔 비슷한 (완전 같을 필요는 없이) 순차 연산이나 큰 자료구조의 요소에서 실행되는 함수들을 실행시키게 한다.”[17] 많은 과학적, 공학적인 응용물들이 자료 병렬화를 보여준다.
루프가 가지고 있는 종속성은 이전 반복의 하나 이상의 결과에 종속된다. 루프의 종속성은 병렬화 루프에 의해 막힌다. 예를 들면 아래의 피보나치 수 의사코드를 보자.
PREV1 := 0
PREV2 := 1
do:
CUR := PREV1 + PREV2
PREV1 := PREV2
PREV2 := CUR
while (CUR < 10)
이 루프는 병렬화할 수 없다. 왜냐하면 CUR 이 각 루프를 도는 동안 그 자신(PREV2)과 PREV1에 종속되기 때문이다. 각 반복이 그 이전 결과에 종속되므로 병렬화할 수 없다. 문제의 크기가 크면 클수록 자료의 병렬화의 유효성은 일반적으로 커진다.[18]
작업 병렬처리[편집]
작업 병렬화는 병렬 프로그램 “전체적으로 다른 계산들은 같거나 다른 자료들에서 실행될 수 있다.”[17] 라는 성질을 가지고 있다. 이것을 자료 병렬화와 상반시키면 계산이 같거나 다른 자료들에서 실행될 수 있다. 작업 병렬화는 일반적인 규모의 문제와 함께 측정되지 않는다.[18]
같이 보기[편집]
참조[편집]
- ↑ Almasi, G.S. and A. Gottlieb (1989). Highly Parallel Computing. Benjamin-Cummings publishers, Redwood City, CA.
- ↑ S.V. Adve et al. (November 2008). "Parallel Computing Research at Illinois: The UPCRC Agenda" Archived 2008년 12월 9일 - 웨이백 머신 (PDF). Parallel@Illinois, University of Illinois at Urbana-Champaign. "The main techniques for these performance benefits – increased clock frequency and smarter but increasingly complex architectures – are now hitting the so-called power wall. The computer industry has accepted that future performance increases must largely come from increasing the number of processors (or cores) on a die, rather than making a single core go faster."
- ↑ Asanovic, Krste et al. (December 18, 2006). pdf "The Landscape of Parallel Computing Research: A View from Berkeley"[깨진 링크(과거 내용 찾기)] (PDF). University of California, Berkeley. Technical Report No. UCB/EECS-2006-183. "Old [conventional wisdom]: Increasing clock frequency is the primary method of improving processor performance. New [conventional wisdom]: Increasing parallelism is the primary method of improving processor performance ... Even representatives from Intel, a company generally associated with the 'higher clock-speed is better' position, warned that traditional approaches to maximizing performance through maximizing clock speed have been pushed to their limit."
- ↑ Patterson, David A. and John L. Hennessy (1998). Computer Organization and Design, Second Edition, Morgan Kaufmann Publishers, p. 715. ISBN 1-55860-428-6.
- ↑ 가 나 Barney, Blaise. “Introduction to Parallel Computing”. Lawrence Livermore National Laboratory. 2013년 6월 29일에 원본 문서에서 보존된 문서. 2007년 11월 9일에 확인함.
- ↑ Rabaey, J. M. (1996). Digital Integrated Circuits. Prentice Hall, p. 235. ISBN 0-13-178609-1.
- ↑ Flynn, Laurie J. "Intel Halts Development of 2 New Microprocessors". The New York Times, May 8, 2004. Retrieved on April 22, 2008.
- ↑ Moore, Gordon E. (1965). “Cramming more components onto integrated circuits” (PDF). 《Electronics Magazine》. 4쪽. 2008년 2월 18일에 원본 문서 (PDF)에서 보존된 문서. 2006년 11월 11일에 확인함.
- ↑ Amdahl, G. (April 1967) "The validity of the single processor approach to achieving large-scale computing capabilities". In Proceedings of AFIPS Spring Joint Computer Conference, Atlantic City, N.J., AFIPS Press, pp. 483–85.
- ↑ Reevaluating Amdahl's Law Archived 2007년 9월 27일 - 웨이백 머신 (1988). Communications of the ACM 31(5), pp. 532–33.
- ↑ Bernstein, A. J. (October 1966). "Program Analysis for Parallel Processing,' IEEE Trans. on Electronic Computers". EC-15, pp. 757–62.
- ↑ Roosta, Seyed H. (2000). "Parallel processing and parallel algorithms: theory and computation". Springer, p. 114. ISBN 0-387-98716-9.
- ↑ Patterson and Hennessy, p. 748.
- ↑ Culler, David E.; Jaswinder Pal Singh and Anoop Gupta (1999). Parallel Computer Architecture - A Hardware/Software Approach. Morgan Kaufmann Publishers, p. 15. ISBN 1-55860-343-3.
- ↑ Culler et al. p. 15.
- ↑ Patt, Yale (April 2004). "The Microprocessor Ten Years From Now: What Are The Challenges, How Do We Meet Them? Archived 2008년 4월 14일 - 웨이백 머신 (wmv). Distinguished Lecturer talk at Carnegie Mellon University. Retrieved on November 7, 2007.
- ↑ 가 나 Culler et al. p. 124.
- ↑ 가 나 Culler et al. p. 125.
외부 링크[편집]
- Lawrence Livermore National Laboratory: Introduction to Parallel ComputingArchived 2013년 6월 10일 - 웨이백 머신
- Designing and Building Parallel Programs, by Ian Foster
- Internet Parallel Computing Archive
- Parallel processing topic area at IEEE Distributed Computing Online
- Parallel Computing Works Free On-line Book Archived 2011년 7월 27일 - 웨이백 머신
- Frontiers of Supercomputing Free On-line Book Covering topics like algorithms and industrial applications
- Universal Parallel Computing Research Center





