뫼비우스 함수
수론과 조합론에서 뫼비우스 함수(Möbius函數, 영어: Möbius function)는 정수가 제곱 인수가 없는 정수인지 여부에 따라 분류하는 곱셈적 함수이다. 뫼비우스 반전 공식에 사용되며, 리만 가설과도 깊은 관계를 가진다. 기호는 .
정의[편집]
뫼비우스 함수
는 양의 정수 을 다음과 같이 가운데 하나에 대응시킨다.
- 이 개의 소인수를 갖는 제곱 인수가 없는 정수라면 이다. (특수한 경우로, 은 0개의 소인수를 가지므로 이다.)
- 이 제곱 인수가 없는 정수가 아니라면, 이다.
즉, 의 소인수 분해가
라면, 뫼비우스 함수는 다음과 같다.
여기서 는 아이버슨 괄호(조건이 참이면 1, 아니면 0)이다.
뫼비우스 함수 은 또한 1의 원시적 제곱근의 합이다.
그렇기 때문에, 1보다 큰 임의의 자연수 n의 모든 약수에 대해서 함숫값을 계산해서 더하면 언제나 0이 된다는 사실도 알 수 있다. 이 사실은 오일러 함수에 대해, 임의의 자연수 n의 모든 약수의 함숫값의 합은 언제나 n이 된다는 정리와 유사하다.
는 양이 아닌 정수에 대하여 일반적으로 정의하지 않는다.
메르텐스 함수(Mertens函數, 영어: Mertens function)는 뫼비우스 함수의 부분합이다. 즉, 다음과 같은 함수이다.
뫼비우스 함수는 1의 원시적 제곱근의 합이므로, 메르텐스 함수를 다음과 같이 정의할 수도 있다.
여기서 은 차 페리 수열이다.
성질[편집]
뫼비우스 함수는 곱셈적 함수이다. 즉, 서로소 정수에 대하여 다음과 같다.
뫼비우스 함수는 디리클레 합성곱 아래 상수 함수 1의 역원이다.
이 성질 때문에 뫼비우스 함수는 뫼비우스 반전 공식에 등장한다.
생성 함수[편집]
뫼비우스 함수의 생성 함수는 다음과 같다.
뫼비우스 함수의 람베르트 급수는 다음과 같다.
이는 에 대하여 수렴한다.
뫼비우스 함수의 디리클레 급수는 리만 제타 함수의 역수이다.
점근적 성질[편집]
뫼비우스 함수의 값이 뿐이므로, 메르텐스 함수는 매우 느리게 움직이며 또한 자명하게
이다.
소수 정리에 따라 다음이 성립한다.
또한, 다음이 성립한다.
즉, 점근적으로 의 수에 대하여 뫼비우스 함수가 +1이며, 의 수에 대하여 뫼비우스 함수가 −1이며, 의 수에 대하여 뫼비우스 함수가 0이다.
리만 가설은 메르텐스 함수에 대한 다음 조건과 동치이다.
메르텐스 추측(Mertens推測, 영어: Mertens conjecture)은 라는 명제이다. 이는 오랫동안 난제로 있었으나, 1985년에 거짓으로 판명되었으며, 다음이 성립한다.[1][2]:188–189
그러나 리만 가설은 현재 (2021년) 미해결 문제이다. 메르텐스 추측보다 더 약하지만 리만 가설보다 더 강한 명제
역시 아직 반증되지 않았으나, 이는 아마 거짓일 것이라고 추측된다.[1]
급수[편집]
뫼비우스 함수에 대하여 다음과 같은 급수가 존재한다.
표[편집]
처음 몇 개의 양의 정수에 대해서 뫼비우스 함수와 메르텐스 함수의 값은 다음과 같다. (OEIS의 수열 A008683), (OEIS의 수열 A002321)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 1 | −1 | −1 | 0 | −1 | 1 | −1 | 0 | 0 | 1 | −1 | 0 | |
| 1 | 0 | −1 | −1 | −2 | −1 | −2 | −2 | −2 | −1 | −2 | −2 |
뫼비우스 함수의 값의 그래프는 다음과 같다.
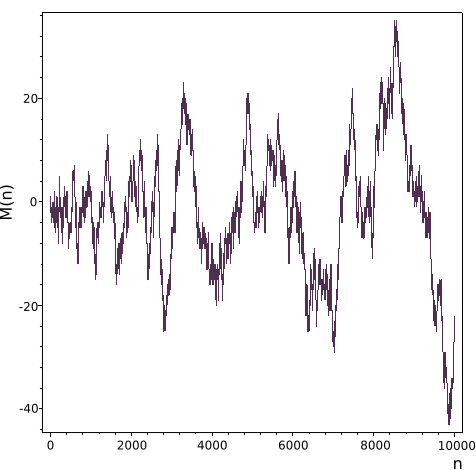
메르텐스 함수의 104까지의 값의 그래프는 다음과 같다.
인 정수 (즉, 제곱 인수가 없는 정수가 아닌 수)은 다음과 같다.
- 4, 8, 9, 12, 16, 18, 20, 24, 25, 27, 28, 32, 36, 40, 44, 45, 48, 49, 50, 52, 54, 56, 60, 63, … (OEIS의 수열 A013929)
역사[편집]
레온하르트 오일러는 1748년 저서[3]에 뫼비우스 함수를 정의하고 암묵적으로 사용하였지만, 자세하게 다루지 않았다.[4]:99, Notes to §3.1 1798년에 카를 프리드리히 가우스는 《산술 연구》(라틴어: Disquisitiones Arithmeticae)[5]에서 1의 원시 거듭제곱근의 합이 이라는 것을 보였으나, 역시 이 함수를 특별히 연구하지 않았다.
1831년에 아우구스트 페르디난트 뫼비우스는 뫼비우스 함수를 최초로 명시적으로 도입하였다.[6][4]:99, Notes to §3.1 1874년에 프란츠 메르텐스가 최초로 오늘날 사용되는 기호 μ를 사용하였다.[7]:53[4]:99, Notes to §3.1
1885년 7월 11일에 토마스 요아너스 스틸티어스는 샤를 에르미트에게 보낸 편지에서 메르텐스 함수를 최초로 사용하였다. (이 편지는 1905년에 출판되었다.[8]) 스틸티어스는 임을 증명하였다고 주장하였고, 또 메르텐스 추측 ()을 추측하였다. 스틸티어스는 뫼비우스 함수를 으로, 메르텐스 함수를 으로 표기하였다. 이 편지에서 스틸티어스는 다음과 같이 적었다.
| “ |
그러나 나는 이 합 에서 항들이 서로 충분히 상쇄하여 가 (임의로 큰 에 대하여) 항상 상계와 하계를 갖는 것을 발견하였습니다. (아마 이 상계와 하계는 +1과 −1로 잡을 수 있을 것입니다.) […]
이와 같이 이 모든 산술 연구는 이 합 에 의존합니다. 나의 증명은 매우 어렵습니다. 나는 연구를 계속하여 이 증명을 더 간략하게 하려고 시도할 것입니다. les termes se compensent assez bien pour que reste toujours comprise entre deux limites fixes, quelque grand que soit (probablement on peut prendre pour ces limites +1 et −1). […] Vous voyez que tout dépend d’une recherche arithmétique sur cette somme . Ma démonstration est bien pénible; je tâcherai, lorsque je reprendrai ces recherches, de la simplifier encore. |
” |
— [8]:162–163
|
그러나 스틸티어스는 이 "증명"을 출판하지 않았다.
1897년에 프란츠 메르텐스는 메르텐스 함수를 독자적으로 재발견하였고, 메르텐스 추측을 스틸티어스와 독자적으로 추측하였다.[9]
1985년에 앤드루 마이클 오들리스코(영어: Andrew Michael Odlyzko, 1949~)와 헤르마뉘스 요하너스 요서프 터 릴러(네덜란드어: Hermanus Johannes Joseph te Riele, 1947~)는 메르텐스 추측이 거짓임을 증명하였다.[1]
같이 보기[편집]
참고 문헌[편집]
- ↑ 가 나 다 Odlyzko, A. M.; te Riele, H. J. J. (1985). “Disproof of the Mertens conjecture” (PDF). 《Journal für die reine und angewandte Mathematik》 (영어) 357: 138–160. doi:10.1515/crll.1985.357.138. ISSN 0075-4102. MR 783538. Zbl 0544.10047.
- ↑ Sándor, József; Mitrinović, Dragoslav S.; Crstici, Borislav, 편집. (2006). 《Handbook of number theory I》. Dordrecht: Springer. 187–189쪽. ISBN 1-4020-4215-9. Zbl 1151.11300.
- ↑ Eulerus, Leonhardus (1748). 《Introductio in analysin infinitorum》 (라틴어). 로잔: Apud Marcum-Michaelem Bousquet & Socios.
- ↑ 가 나 다 Shapiro, Harold N. (1983). 《Introduction to the Theory of Numbers》 (영어). Wiley. ISBN 0-471-86737-3.
- ↑ Gavss, Carolus Fridericus (1801). 《Disqvisitiones arithmeticae》 (라틴어). 라이프치히: in commissis apvd Gerh. Fleischer, Jun.
- ↑ Möbius, A. F. (1832). “Über eine besondere Art von Umkehrung der Reihen”. 《Journal für die reine und angewandte Mathematik》 (독일어) 1832 (9): 105-123. doi:10.1515/crll.1832.9.105. ISSN 0075-4102. Zbl 009.0333cj.
- ↑ Mertens, F. (1874). “Ein Beitrag zur analytischen Zahlentheorie”. 《Journal für die reine und angewandte Mathematik》 (독일어) 1874 (78): 46–62. doi:10.1515/crll.1874.78.46. ISSN 0075-4102. JFM 06.0116.01.
- ↑ 가 나 Stieltjes, T. J. (1905). 〈79. Stieltjes a Hermite. Paris, 11 juillet 1885〉. B. Baillaud, H. Bourget. 《Correspondance d’Hermite et Stieltjes》 (프랑스어). 파리: Gauthier-Villars. 160–164쪽.
- ↑ Mertens, F. (1897). “Ueber eine zahlentheoretische Function”. 《Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften, Mathematisch-Naturwissenschaftliche Klasse, Abteilung 2a》 (독일어) 106: 761–830. JFM 28.0177.01.
외부 링크[편집]
- “Möbius function”. 《Encyclopedia of Mathematics》 (영어). Springer-Verlag. 2001. ISBN 978-1-55608-010-4.
- Weisstein, Eric Wolfgang. “Möbius function”. 《Wolfram MathWorld》 (영어). Wolfram Research.
- Weisstein, Eric Wolfgang. “Mertens function”. 《Wolfram MathWorld》 (영어). Wolfram Research.
- Weisstein, Eric Wolfgang. “Mertens conjecture”. 《Wolfram MathWorld》 (영어). Wolfram Research.
- Lipton, R. J. (2011년 2월 23일). “The depth of the Möbius function”. 《Gödel’s Lost Letter and P=NP》 (영어).
- Tao, Terence (2015년 9월 6일). “Sign patterns of the Möbius and Liouville functions”. 《What’s New》 (영어).
- “Möbius function”. 《OeisWiki》 (영어).
- “뫼비우스 뮤 함수”. 《오메가》.[깨진 링크(과거 내용 찾기)]












![{\displaystyle \mu (n)=(-1)^{\sum _{p}n_{p}}\prod _{p}[n_{p}\leq 1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/625c61c055ae01d9a29facf78a0260009c96333f)
![{\displaystyle [\cdots ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51cc669ab2e6cf8641bcb1c0fa1c283d463b21e4)