수학에서 드무아브르의 공식(영어: de Moivre’s formula) 또는 드무아브르의 정리(de Moivre's theorem)는 임의의 복소수를 극형식으로 나타내었을 때 성립하는 다음 등식을 의미한다. 이 식에서 i는 허수 단위를 뜻한다.

이 공식은 복소수와 삼각 함수간의 관계를 보여준다.
 가 실수라는 가정하에, 좌변을 전개하면 실수부와 허수부로 나눌 수 있다. 이를 이용하면
가 실수라는 가정하에, 좌변을 전개하면 실수부와 허수부로 나눌 수 있다. 이를 이용하면  만을 사용하여
만을 사용하여  와
와  을 나타내는 식을 쉽게 유도할 수 있다. 뿐만 아니라,
을 나타내는 식을 쉽게 유도할 수 있다. 뿐만 아니라,  의 복소근을 쉽게 구할 수 있다.
의 복소근을 쉽게 구할 수 있다.
역사적으로 오일러의 공식보다도 더 먼저 증명되었지만, 오일러 공식을 사용하면 이를 쉽게 유도할 수 있다.

지수 함수의 성질에 의하여 다음 식을 얻을 수 있다.

그러면, 오일러의 공식에 의하여 다음 식을 얻을 수 있다.

수학적 귀납법을 이용한 증명[편집]
세 가지 경우로 나누어 생각한다.
 인 정수에 대하여, 수학적 귀납법을 사용하여 이를 증명할 수 있다.
인 정수에 대하여, 수학적 귀납법을 사용하여 이를 증명할 수 있다.  일 때, 이 등식은 참이다. 이제
일 때, 이 등식은 참이다. 이제  일 때 다음의 식이 성립한다고 가정하자.
일 때 다음의 식이 성립한다고 가정하자.

이제  일 때 식이 성립하는지를 확인하면,
일 때 식이 성립하는지를 확인하면,

이 식이  일 때도 참이라는 것을 알 수 있다. 따라서 수학적 귀납법에 의하여
일 때도 참이라는 것을 알 수 있다. 따라서 수학적 귀납법에 의하여  인 모든 양의 정수에 대하여 식이 성립한다.
인 모든 양의 정수에 대하여 식이 성립한다.
이제  일 때 공식이 성립하는지를 확인하여 보면,
일 때 공식이 성립하는지를 확인하여 보면,  또는
또는  라는 약속에 의하여 성립한다.
라는 약속에 의하여 성립한다.
이제  일 때 공식이 성립하는지를 확인하여 보자. 우선
일 때 공식이 성립하는지를 확인하여 보자. 우선  을 만족하는 양의 정수
을 만족하는 양의 정수  에 대하여 생각하여 보면,
에 대하여 생각하여 보면,

이 식이 모든 정수에 대하여 성립한다는 사실을 알 수 있다.
코사인과 사인 부분을 각각 증명하는 방법[편집]
복소수의 성질에 의하여, 두 복소수가 같으려면 실수부와 허수부가 같아야 한다.
만약  와
와  가 실수라면, 아래와 같은 식을 얻을 수 있다.
가 실수라면, 아래와 같은 식을 얻을 수 있다.

이 식은  가 복소수일 때에도 양변이 정칙함수이므로, 그 성질에 의하여 성립한다. 위의 식이 실제로 성립하는지 확인해보기 위해
가 복소수일 때에도 양변이 정칙함수이므로, 그 성질에 의하여 성립한다. 위의 식이 실제로 성립하는지 확인해보기 위해  을 대입해보면,
을 대입해보면,

 에 대한 등식의 우변은, 실제로는 체비쇼프 다항식
에 대한 등식의 우변은, 실제로는 체비쇼프 다항식  의 값이다.
의 값이다.
일반화[편집]
이 공식은 더 일반적으로 확장할 수 있다.  와
와  가 복소수라면,
가 복소수라면,  와는 달리
와는 달리

는 여러값 함수(multivalued function)이다. 따라서

는  의 여러 값중 하나일 뿐이다.
의 여러 값중 하나일 뿐이다.
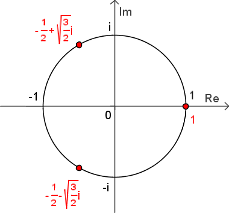 복소평면위에 찍은
복소평면위에 찍은  의 근.
의 근.
이 공식은  의 복소근을 구하는 데에 활용할 수 있다. 만약
의 복소근을 구하는 데에 활용할 수 있다. 만약  가 복소수라면, 이는 극형식 형태로 다음과 같이 쓸 수 있다.
가 복소수라면, 이는 극형식 형태로 다음과 같이 쓸 수 있다.

이 때  가 정수라면,
가 정수라면,
![{\displaystyle w^{{}^{\frac {1}{n}}}=\left[r\left(\cos x+i\sin x\right)\right]^{{}^{\frac {1}{n}}}=r^{{}^{\frac {1}{n}}}\left[\cos \left({\frac {x+2k\pi }{n}}\right)+i\sin \left({\frac {x+2k\pi }{n}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a2f080016d8de52eef64c247beb8c9bceb1192b)
 개의 서로 다른 근을 구할 때,
개의 서로 다른 근을 구할 때,  부터
부터  까지의 값을 대입해주면 쉽게 그 값을 구할 수 있다.
까지의 값을 대입해주면 쉽게 그 값을 구할 수 있다.
또한 이 공식은 고차방정식의 특수형태인,  의 꼴로, 이항방정식 이되겠다.
의 꼴로, 이항방정식 이되겠다.
아브라암 드무아브르가 발견하였다. 허수에 대한 직접적인 언급은 없다.[1][2]
같이 보기[편집]
참고 문헌[편집]
- Milton Abramowitz and Irene A. Stegun, Handbook of Mathematical Functions, (1964) Dover Publications, New York. ISBN 0-486-61272-4. (p. 74).
외부 링크[편집]








































![{\displaystyle w^{{}^{\frac {1}{n}}}=\left[r\left(\cos x+i\sin x\right)\right]^{{}^{\frac {1}{n}}}=r^{{}^{\frac {1}{n}}}\left[\cos \left({\frac {x+2k\pi }{n}}\right)+i\sin \left({\frac {x+2k\pi }{n}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a2f080016d8de52eef64c247beb8c9bceb1192b)



