스타인메츠 다면체

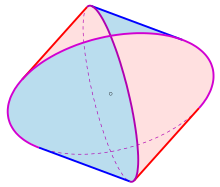
기하학에서 스타인메츠 다면체는 반지름이 같고 서로 수직인 원기둥 두세 개가 교차되어 만들어진 다면체이다. 이것은 스타인메츠가 연구하기 오래 전부터 알려져 있었지만 그 부피를 계산한 찰스 프로테우스 스타인메츠의 이름을 따와서 이름을 정했다.^[1]

원기둥 두 개가 교차되었을 때, 겹치는 부분은 바이실린더 또는 무헤팡가이(정사각형 우산 두개라는 의미의 중국어이다.^[2] 중국어로 쓰면 牟合方蓋이다)라고 부른다. 위상적으로는 사각 호소헤드론으로 볼 수 있다. 원기둥 세 개가 교차되면, 겹치는 부분을 트라이실린더라고 부른다.

바이실린더

부피

바이실린더는 위상적으로 사각 호소헤드론과 동일하다. 아르키메데스와 조충지는 두 원기둥의 반지름이 r인 바이실린더의 부피를 계산했다:

{\frac {16}{3}}r^{3}

원기둥 두 개가 교차할 때, 전체 부피는 원기둥 두 개의 부피에 겹치는 부분의 부피 (또는 여기서는 이등분)를 빼서 계산할 수 있다.

바이실린더(흰색)의 부피를 유도하는 것은 정육면체(빨간색)에 채워서 이뤄진다. 바이실린더와 교차하는 (원기둥의 축과 평행한) 평면은 정사각형을 만들고 큰 정육면체와 교차한 것은 큰 정사각형을 만든다. 두 사각형의 면적 차이는 작은 정사각형(파란색) 4개의 면적과 같다. 평면이 이 물체를 통과할 때, 이 파란 사각형은 정육면체의 구석의 이등변 삼각형 옆면으로 가지는 사각뿔로 나타낼 수 있다; 이 사각뿔의 꼭대기는 네 정육면체 모서리의 중점에 위치한다. 바이실린더 전체를 통과해 움직이는 면은 총 8개의 각뿔을 만든다.

정육면체(빨간색)의 부피 빼기 각뿔(파란색) 8개의 부피는 바이실린더(흰색)의 부피이다. 각뿔 8개의 부피는 $\textstyle 8\times {\frac {1}{3}}r^{2}\times r={\frac {8}{3}}r^{3}$ 이므로 바이실린더의 부피를 계산하면 $\textstyle (2r)^{3}-{\frac {8}{3}}r^{3}={\frac {16}{3}}r^{3}$ 이다.

표면적

표면적은 16r²이다. 표면적과 부피의 비 ${\tfrac {r}{3}}$ 은 일반적으로 구에 외접하는 형태족에 적용된다. 이것에는 구 자신과, 원기둥, 정육면체, 그리고 스타인메츠 다면체 두 종류를 포함한다(Apostol and Mnatsakanian 2006).

바이실린더의 표면은 타원의 인 곡선 네 개로 나뉜 원기둥형 패치 네 개로 이루어져있다. 네 개의 패치와 네 개의 구분하는 곡선은 서로 반대쪽에 있는 꼭짓점 두 개에서 만난다.

파생된 다면체

이등분된 바이실린더는 볼트^[3], 그리고 이 모양의 건축물을 클로이스터 볼트라고 부른다.

트라이실린더

트라이실린더는 조합적으로 마름모십이면체와 동등한 타원 호로 연결된 꼭짓점 14개를 가진다. 이것의 부피는 다음과 같다:

(16-8{\sqrt {2}})r^{3}\,

그리고 표면적은 다음과 같다:

3(16-8{\sqrt {2}})r^{2}.\,

더 많은 원기둥

네 개의 원기둥으로는, 정사면체의 꼭짓점과 그 반대편 위치의 점을 잇는 축을 따라 있는 다면체의 부피는 다음과 같다:

12(2{\sqrt {2}}-{\sqrt {6}})r^{3}\,

여섯 개의 원기둥으로는, 축이 정육면체의 면의 대각선과 평행한 다면체의 부피는 다음과 같다:

{\frac {16}{3}}(3+2{\sqrt {3}}-4{\sqrt {2}})r^{3}\,

각주

↑ Howard Eves, Slicing it thin, in: David Klarner, The mathematical Gardner, Wadsworth International 1981, S. 111
↑ http://thesaurus.maths.org/mmkb/entry.html?action=entryByConcept&id=3736^{[깨진 링크(과거 내용 찾기)]}
↑ Weisstein, Eric W. (c. 1999–2009). “Steinmetz Solid”. 《MathWorld—A Wolfram Web Resource》. Wolfram Research, Inc. 2009년 6월 9일에 확인함.

서지학

Apostol, Tom M.; Mnatsakanian, Mamikon A. (2006). “Solids circumscribing spheres” (PDF). 《American Mathematical Monthly》 113 (6): 521–540. doi:10.2307/27641977. JSTOR 27641977. MR 2231137. 2012년 2월 7일에 원본 문서 (PDF)에서 보존된 문서. 2017년 11월 14일에 확인함.
Jan Hogendijk (2002). “The surface area of the bicylinder and Archimedes' Method”. 《Historia Math.》 29 (2): 199–203. doi:10.1006/hmat.2002.2349. MR 1896975.
Moore, M. (1974). “Symmetrical intersections of right circular cylinders”. 《The Mathematical Gazette》 58 (405): 181–185. doi:10.2307/3615957. JSTOR 3615957.

외부 링크

A 3D model of Steinmetz solid in Google 3D Warehouse 보관됨 2013-01-24 - archive.today
Weisstein, Eric Wolfgang. “Steinmetz Solid”. 《Wolfram MathWorld》 (영어). Wolfram Research.

[1] Howard Eves, Slicing it thin, in: David Klarner, The mathematical Gardner, Wadsworth International 1981, S. 111

[2] ttp://thesaurus.maths.org/mmkb/entry.html?action=entryByConcept&id=3736^{[깨진 링크(과거 내용 찾기)]}

[3] Weisstein, Eric W. (c. 1999–2009). “Steinmetz Solid”. 《MathWorld—A Wolfram Web Resource》. Wolfram Research, Inc. 2009년 6월 9일에 확인함.

[1]

[2]

[3]