SEIR 모형

SEIR 모형은 역학에서 전염병의 확산을 설명할 때 수학적인 모델링을 통해 접근할 수 있는 방법 중 하나이다. 이 모형은 SIR 모형보다는 더 현실에 가깝다고 여겨지며, 이는 병에 막 감염된 개체가 당장은 다른 개체에게 병을 옮기지 않는다는 점을 고려하기 때문이다. 개체에 기반한 모형보다는 거시적으로 개체군 전체를 조명하는 방식에 가깝다.

방정식[편집]

N 개체로 이루어진 개체군을 S, E, I, R의 네 그룹으로 나누어

S+E+I+R=1.

혹은

NS+NE+NI+NR=N.

의 공식이 성립되도록 한다.

모든 개체는

Susceptible (S, 감염대상군) → Exposed (E, 접촉군) → Infectious (I, 감염군) → Recovered (R, 회복군)

의 단계를 거친다. 전염병의 확산은 다음과 같이 설명될 수 있다.

{\begin{aligned}{\frac {\mathrm {d} S}{\mathrm {d} t}}&=-\beta SI,\\{\frac {\mathrm {d} E}{\mathrm {d} t}}&=\beta SI-aE,\\{\frac {\mathrm {d} I}{\mathrm {d} t}}&=aE-\gamma I,\\{\frac {\mathrm {d} R}{\mathrm {d} t}}&=\gamma I.\end{aligned}}

이것은 상미분방정식의 비선형 시스템에 속한다. 문헌에서는 여러 형태의 공식을 발견할 수 있는데 예를 들면 ${\frac {\beta SI}{N}}$ 항을 $\beta SI$ 대신 쓰는 식이다. 이외에도 $S+E+I+R$ 의 합을 반드시 $1$ 이라고 정하는 대신 N을 전체 개체군이라 할 때 $N=S+E+I+R$ 라고 정의할 수도 있다.

수량	단위	설명
`S`(`t`)	1	감염대상군 (Susceptible): 감염될 수 있으나 아직 감염되지 않은 개체의 수
`E`(`t`)	1	접촉군 (Exposed): 이미 감염되었으나 아직 병을 전염시키지는 않는 단계에 있는 개체의 수
`I`(`t`)	1	감염군 (Infectious): 병을 전염시킬 수 있는 개체의 수
`R`(`t`)	1	회복군 (Recovered 또는 Resistent): 병에서 회복한 개체의 수와 격리 중 사망한 개체의 수의 합
`t`	d	시간 (일)
`β`	1/d	감염률 (Transmission rate). 역수는 접촉 평균 시간과 같다.
`γ`	1/d	회복률 (Recovery rate). 역수는 평균 전염 가능 시간과 같다.
`a`	1/d	역수는 평균 지연 시간 (latency)과 같다.

평균 지연 시간은 접촉군 (Exposed)의 한 개체가 병을 전염시킬 수 있게 되어 감염군으로 분류되기까지의 평균 시간을 나타내며 잠복기와는 다른데 이는 증상의 발현과 병을 전염시킬 수 있는 능력이 갖춰지는 것을 동치할 수 없기 때문이다. 감염률은 접촉률 (contact rate)로 불리기도 하는데, 더 상세하게는 $\beta =pc$ 로 $p$ 는 감염 확률을, c는 접촉률을 나타낸다.

기초감염재생산수와의 관계[편집]

병의 확산이 멈추려면 ${\frac {\mathrm {d} E}{\mathrm {d} t}}=0$ 와 ${\frac {\mathrm {d} I}{\mathrm {d} t}}=0$ 의 조건이 성립해야 한다. 이 조건들을 방정식에 대입하면 $aE=\beta SI$ 와 $aE=\gamma I$ 가 되므로 $\beta S=\gamma$ 라는 결과가 도출된다. 이는 기초감염재생산수 $R_{0}=1$ 의 경우와 같고 $S_{0}=N$ 이라고 하면^[1]^[2]

R_{0}={\frac {\beta N}{\gamma }}

가 된다. $N=1$ 일 때 정규화된 인명 수나 변형된 SEIR 공식을 사용하면 (SIR 모형에도 적용할 수 있으나 $R_{0}$ 를 구하는 공식에서 $\beta$ 의 정의가 다르다)

R_{0}=\beta /\gamma

.^[3]^[4]

중간 단계로의 이행을 나타내는 매개변수 $a$ 는 접촉군에 속한 환자가 사망할 가능성을 무시할 경우 기초감염재생산수에 영향을 주지 않는다.^[1]

시간에 영향을 받는 순감염재생산수 (net reproduction number)는 $q=1-S$ 일 때, $R_{q}=R_{0}\cdot S$ 또는 $R_{q}=\left(1-q\right)\cdot R_{0}$ 로 정의할 수 있다.

최대 감염자 비율[편집]

기초감염재생산수는 개체군의 최대 감염자 비율에 큰 영향을 준다. 병에 감염된 개체 전체를 $J$ 라고 하고 $J(t)=E(t)+I(t)$ 이면 위의 미분방정식에 의해

{\frac {\mathrm {d} J}{\mathrm {d} S}}={\frac {\mathrm {d} E+\mathrm {d} I}{\mathrm {d} S}}={\frac {-\gamma I+\beta SI}{-\beta SI}}={\frac {\gamma }{\beta S}}-1

,

또는 기초감염재생산수 $R_{0}={\frac {\beta }{\gamma }}$ 일 때

{\frac {\mathrm {d} J}{\mathrm {d} S}}={\frac {1}{R_{0}S}}-1.

가 된다. 이 방정식을 $\mathrm {d} J={\frac {\mathrm {d} S}{R_{0}S}}-\mathrm {d} S$ 로 바꾸고 변수분리법을 통한 적분에 의해 모든 t에 적용되는

J(t)+S(t)-{\frac {1}{R_{0}}}\ln S(t)={\text{const}}

가 도출되는데 여기서 $\ln$ 은 자연로그를 뜻한다. 따라서

J(t)+S(t)-{\frac {1}{R_{0}}}\ln S(t)=J(0)+S(0)-{\frac {1}{R_{0}}}\ln S(0)

혹은

J(t)=J(0)+S(0)-{\frac {1}{R_{0}}}\ln S(0)+\underbrace {{\frac {1}{R_{0}}}\ln S(t)-S(t)} _{=:\ f(S(t))}.

가 성립한다. 도움 함수 $f(x)={\frac {1}{R_{0}}}\ln x-x$ 는 $f'(x)={\frac {1}{R_{0}x}}-1$ 이므로 최대값이 $x={\frac {1}{R_{0}}}$ 이다. 최대 감염자 비율 $J_{\max }$ 에는 $S(t)={\frac {1}{R_{0}}}$ 일 때 도달하게 되며, 따라서 $J_{\max }$ 는 기초감염재생산수와 초기값 $J$ 및 $S$ 만의 영향을 받는다:

J_{\text{max}}=J(0)+S(0)-{\frac {1}{R_{0}}}\ln S(0)-{\frac {1}{R_{0}}}+{\frac {1}{R_{0}}}\ln {\frac {1}{R_{0}}}=J(0)+S(0)+{\frac {1}{R_{0}}}\left(\ln {\frac {1}{R_{0}S(0)}}-1\right).

아직 알려지지 않은 바이러스 등에 의해 새로이 등장하는 전염병의 경우 $S(0)=1$ 이고 $J(0)=0$ 으로 설정되고 최대 감염자 비율과 기초감염재생산수의 관계는 다음과 같아진다.

J_{\text{max}}=1+{\frac {1}{R_{0}}}\left(\ln {\frac {1}{R_{0}}}-1\right).

이 공식은 SIR 모형의 최대 감염자 비율을 구하는 공식과 일치한다.

전염병 유행 말기 회복된 개체의 비율[편집]

격리가 전혀 없이 전염병이 유행할 경우 개체군 내에서 감염된 전체 개체의 비율도 기초감염재생산수와 상관 관계가 있다. 미분방정식으로 나타낼 경우

{\frac {\mathrm {d} S}{\mathrm {d} R}}={\frac {S'(t)}{R'(t)}}=-{\frac {\beta S}{\gamma }}=-R_{0}S.

이고 초기값이 $R(0)=0$ 라면

S(t)=S(0){\mathrm {e} }^{-R_{0}R(t)}.

이다. $t\to \infty$ 일 경우 $E=I=0$ 이고 따라서 $S+R=1$ 이 된다. 여기서

1-q=S(0){\mathrm {e} }^{-R_{0}q},\quad q:=\lim _{t\to \infty }R(t).

를 도출할 수 있고 다음과 같은 공식에 이르게 된다.

-R_{q}{\mathrm {e} }^{-R_{q}}=(q-1)R_{0}{\mathrm {e} }^{(q-1)R_{0}}=-S(0)R_{0}{\mathrm {e} }^{-R_{0}}.

$x:=-S(0)R_{0}\mathrm {e} ^{-R_{0}}$ 이고 $y:=(q-1)R_{0}$ 라고 했을 때 최종적인 공식은 $y\mathrm {e} ^{y}=x$ 가 되고 람베르트 W 함수 $W(x)$ 를 활용해 $y=W(x)$ 로 바꾼 뒤 역치환하는 과정을 거쳐

q=1+{\frac {1}{R_{0}}}W(-S(0)R_{0}{\mathrm {e} }^{-R_{0}})

에 도달하게 된다.

W 함수의 필요한 부분을 계산하려면 $f(w):=w\mathrm {e} ^{w}-x$ 함수의 2차 테일러 다항식에 −1 을 넣고 영점을 구한 뒤 고정 소수점 반복을 $w\mapsto x\mathrm {e} ^{-w}$ 로 한차례 적용한다. 그 결과물은

w=x\exp(1-{\sqrt {2\mathrm {e} x+2}}).

이다. W 함수의 가까운 근사치는

W(x)\approx \varphi ^{n}(w),

에 의해 얻을 수 있고 여기서 $\varphi ^{n}$ 는 뉴턴 방법의 n 번째 반복인

\varphi (w)=w-{\frac {f(w)}{f'(w)}}={\frac {x\mathrm {e} ^{-w}+w^{2}}{w+1}}

을 뜻한다. 현실의 전염병에 적용할 때는 $n=4$ 이면 충분하다.

기하급수적 초기 단계[편집]

전염병의 초기 단계에서는 확산이 기하급수적인 형태에 가깝게 일어난다. $I=I(0){\mathrm {e} }^{\lambda t}$ 을 가정한다면 $I'=\lambda I$ 역시 참이 된다. 그에 따라 $aE=\gamma I+\lambda I$ 와 $R=\gamma I/\lambda$ 이 성립하며 따라서

1-S=E+I+R={\frac {\gamma +\lambda }{a}}I+I+{\frac {\gamma }{\lambda }}I={\Big (}{\frac {\gamma +\lambda }{a}}+1+{\frac {\gamma }{\lambda }}{\Big )}I.

라는 결과가 나온다. 이 방정식을 양쪽 다 미분한 후 $-S'=\beta SI$ 로 치환하고 $I$ 로 나누면

\beta S={\Big (}{\frac {\gamma +\lambda }{a}}+1+{\frac {\gamma }{\lambda }}{\Big )}\lambda

혹은

a\beta S=(\lambda +a)(\lambda +\gamma ).

를 얻게 된다. 초기에는 $S\approx 1$ 가 상당히 정확한 근삿값이므로 $S=1$ 이 성립하고 매개변수 $a,\beta ,\gamma$ 와 증식상수 $\lambda$ 의 관계를 알아낼 수 있다.

다른 체계적 접근법으로는 $S$ 를 곧바로 1로 정의하고 미분방정식을 연립 일차 방정식으로 단순화하여

{\begin{pmatrix}E'\\I'\end{pmatrix}}={\begin{pmatrix}-a&\beta \\a&-\gamma \end{pmatrix}}{\begin{pmatrix}E\\I\end{pmatrix}}

로 설명하는 것이 가능하다.^[5] 다른 접근 방법들도 고정계수와 고유값&고유벡터를 활용한 선형 상미분방정식에 기반한다. 증식상수는 계수행렬 $J:={\big (}{\begin{smallmatrix}-a&\beta \\a&-\gamma \end{smallmatrix}}{\big )}$ 의 고유값으로 이미 발견한 방정식은

0=\det \left(J-\lambda {\begin{pmatrix}1&0\\0&1\end{pmatrix}}\right)=(a+\lambda )(\gamma +\lambda )-a\beta .

에 의해 구할 수 있다. 모든 기하급수적 증식과정에서와 마찬가지로 증식상수 $\lambda$ 는 더 이해가 쉽게

T_{n}={\frac {\ln(n)}{\lambda }},

를 통해 수 배의 증식이 이루어지기까지의 시간으로 나타낼 수 있으며, 이는 특히 배가시간 $T_{2}$ 에도 적용 가능하다.

예시[편집]

다음은 독일의 코로나19 범유행을 모델링할 때 쓰인 매개변수를 파이썬에서 그대로 적용한 예시이다.^[6] 전염병의 확산은 기초감염재생산수 $=2.4$ 를 토대로 이루어지고, 이는 중요한 격리 조치들이 취해지지 않았을 경우에 해당한다. 기초값 문제를 수치적으로 푸는데는 오일러 방법이면 충분하다.

from numpy import array as vector

# Explicit Euler method
def euler_method(f,t0,x0,t1,h):
    t = t0; x = x0
    a = [[t,x]]
    for k in range(0,1+int((t1-t0)/h)):
        t = t0 + k*h
        x = x + h*f(t,x)
        a.append([t,x])
    return a

def SEIR_model(beta,gamma,a):
    def f(t,x):
        S,E,I,R = x
        return vector([
            -beta*S*I,
            beta*S*I - a*E,
            a*E - gamma*I,
            gamma*I
        ])
    return f

def SEIR_simulation(beta,gamma,a,E0,I0,days,step=0.1):
    x0 = vector([1.0-E0-I0,E0,I0,0.0])
    return euler_method(SEIR_model(beta,gamma,a),0,x0,days,step)

def diagram(simulation):
    import matplotlib.pyplot as plot
    plot.style.use('fivethirtyeight')
    figure,axes = plot.subplots()
    figure.subplots_adjust(bottom = 0.15)
    axes.grid(linestyle = ':', linewidth = 2.0, color = "#808080")
    t,x = zip(*simulation())
    S,E,I,R = zip(*x)
    axes.plot(t,S, color = "#0000cc")
    axes.plot(t,E, color = "#ffb000", linestyle = '--')
    axes.plot(t,I, color = "#a00060")
    axes.plot(t,R, color = "#008000", linestyle = '--')
    plot.show()

def simulation1():
    N = 83200000 # Einwohnerzahl von Deutschland 2019/2020
    R0 = 2.4; gamma = 1/3.0
    return SEIR_simulation(
        beta = R0*gamma, gamma = gamma, a = 1/5.5,
        E0 = 40000.0/N, I0 = 10000.0/N, days = 140)

diagram(simulation1)

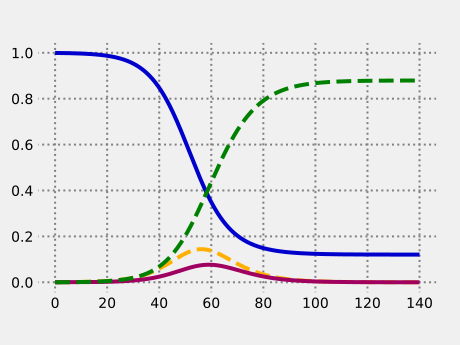
S, E, I, R의 네 군이 전체 개체군에서 차지하는 비율을 날짜별로 계산한 결과. `S`는 청색, `E`는 노란색 점선, `I`는 자홍색, `R`는 녹색 점선으로 표시.

여기서 볼 수 있는 것은 전염병이 면역임계치 (critical immune threshold)

q_{c}=1-{\frac {1}{R_{0}}}=58\,\%

에 도달한 다음에도 감염군에 의해 계속 전파된다는 점이다. 다만 전염병이 면역임계치에 도달한 후에는 약 한달간의 강력한 격리 조치를 통해 멈추도록 만들 수 있을 것이다.

인구통계역학을 포함할 경우[편집]

사망률 $\mu$ 를 상수로 두고 이에 상응하는 출생률과 함께 모형을 확장시킨

{\begin{aligned}S'&=\mu -\beta SI-\mu S,\\E'&=\beta SI-aE-\mu E,\\I'&=aE-\gamma I-\mu I,\\R'&=\gamma I-\mu R\end{aligned}}

공식도 있다. 원래 SEIR 모형과는 다르게 전염병의 풍토병화를 전제하며

S'=E'=I'=R'=0

라고 정의한 평형에 이르기까지 감염대상군 $S$ 에서는 진동이 올 수도 있다.

기초감염재생산수는 여기서 평형 상태를 놓고 볼 때 다음과 같이 정의할 수 있다.

R_{0}={\frac {\beta a}{(\mu +a)(\mu +\gamma )}}.

시간의존적 전염률 (Time-dependent transmission rate)[편집]

전염병을 대하는 태도의 변화, 격리와 계절성은 전염률의 변화를 가져오고, 이는 전염률을 시간의존적 함수 $\beta (t)$ 로 모델링할 때 고려되는 사안이다. 이 때에도 다른 모형들은 달라지지 않는다.^[7] 계절성을 가장 단순하게 모델링하는 방법으로는 사인 진동 (sine oscillation) 형태로 날씨가 추운 달에는 전염률이 높고 따뜻한 달에는 전염률이 낮게 나오는 것을 가정할 수가 있다.^[8]

명백한 시간의존도를 가진 미분방정식 체계는 자생적이지 않고 따라서 더 이상 직접적으로 역동적인 체계라고 할 수 없다. 다만 $t'=1$ 의 추가를 통해 인위적으로 자생적인 체계를 갖출 수는 있다.

외부 링크[편집]

SEIR 모형 계산기 전염병의 경과를 SEIR 모형과 변수의 자유로운 입력을 통해 시뮬레이션하기

참고 문헌[편집]

Matt J. Keeling, Pejman Rohani: Modeling Infectious Diseases in Humans and Animals. Princeton University Press, 2008.
Matthias an der Heiden, Udo Buchholz: Modellierung von Beispielszenarien der SARS-CoV-2-Epidemie 2020 in Deutschland. Robert Koch-Institut, Abteilung für Infektionsepidemiologie (20. März 2020). DOI:10.25646/6571.2.

각주[편집]

↑ ^가 ^나 Pauline van den Driessche, Reproduction numbers of infectious disease models, Infectious Disease Modelling, Band 2, August 2017, S. 288–303
↑ Odo Diekmann, Hans Heesterbeek, Tom Britton, Mathematical tools for understanding infectious disease dynamics, Princeton UP, 2013, S. 35
↑ Institute for Desease Modeling: SEIR Model Archived 2020년 5월 7일 - 웨이백 머신
↑ C. Hubbs (2020): Social Distancing to Slow the Coronavirus^{[깨진 링크(과거 내용 찾기)]}
↑ Junling Ma: Estimating epidemic exponential growth rate and basic reproduction number. In: Infectious Disease Modelling, Volume 5, 2020, S. 129–141, KeAi Publishing (17. Dec. 2019).
↑ “Stellungnahme der Deutschen Gesellschaft für Epidemiologie (DGEpi) zur Verbreitung des neuen Coronavirus (SARS-CoV-2)” (PDF). 2020년 3월 20일에 원본 문서 (PDF)에서 보존된 문서. 2020년 6월 18일에 확인함. Die aktuelle Version siehe hier Archived 2020년 5월 29일 - 웨이백 머신.
↑ Gerardo Chowell, Cécile Viboud, Lone Simonsen, Seyed M. Moghadas: Characterizing the reproduction number of epidemics with early subexponential growth dynamics Archived 2020년 6월 19일 - 웨이백 머신. In: J. R. Soc. Interface 13: 20160659 (17. August 2016). DOI: 10.1098/rsif.2016.0659.
↑ M. Keeling, P. Rohani: Modeling Infectious Diseases in Humans and Animals. Abschnitt 5.2. (S. 159): Modeling forcing in childhood infectious diseases: Measles.

[driesche-1] 가 ^나 Pauline van den Driessche, Reproduction numbers of infectious disease models, Infectious Disease Modelling, Band 2, August 2017, S. 288–303

[2] Odo Diekmann, Hans Heesterbeek, Tom Britton, Mathematical tools for understanding infectious disease dynamics, Princeton UP, 2013, S. 35

[idm-seir-3] Institute for Desease Modeling: SEIR Model Archived 2020년 5월 7일 - 웨이백 머신

[4] C. Hubbs (2020): Social Distancing to Slow the Coronavirus^{[깨진 링크(과거 내용 찾기)]}

[5] Junling Ma: Estimating epidemic exponential growth rate and basic reproduction number. In: Infectious Disease Modelling, Volume 5, 2020, S. 129–141, KeAi Publishing (17. Dec. 2019).

[dgepi-2020-03-19-6] “Stellungnahme der Deutschen Gesellschaft für Epidemiologie (DGEpi) zur Verbreitung des neuen Coronavirus (SARS-CoV-2)” (PDF). 2020년 3월 20일에 원본 문서 (PDF)에서 보존된 문서. 2020년 6월 18일에 확인함. Die aktuelle Version siehe hier Archived 2020년 5월 29일 - 웨이백 머신.

[7] Gerardo Chowell, Cécile Viboud, Lone Simonsen, Seyed M. Moghadas: Characterizing the reproduction number of epidemics with early subexponential growth dynamics Archived 2020년 6월 19일 - 웨이백 머신. In: J. R. Soc. Interface 13: 20160659 (17. August 2016). DOI: 10.1098/rsif.2016.0659.

[8] M. Keeling, P. Rohani: Modeling Infectious Diseases in Humans and Animals. Abschnitt 5.2. (S. 159): Modeling forcing in childhood infectious diseases: Measles.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]