유한요소법

2D FEM solution for a magnetostatic configuration (lines denote the direction of calculated flux density and colour - its magnitude)

2D mesh for the image above (mesh is denser around the object of interest)

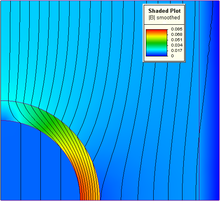
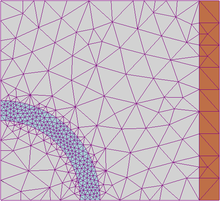
유한요소법(有限要素法, 영어: finite element method, 약자 FEM)은 수학용어로, 편미분 방정식이나 적분, 열 방정식 등의 근사해를 구하는 한 방법이다. 해석 접근은 정적인 문제에서 미분 방정식을 제거하거나, 편미분 방정식을 상미분 방정식으로 변환하는 것으로 접근을 한다. 접근법은 유한미분에서 사용되는 기법과 동일하다.

편미분 방정식을 풀기 위한 선행 작업으로는 대상식을 예측할 수 있는 식을 만드는 것이다. 그러나 수치적 안정(벡터합과 같이 서로 평형을 이루는 경우)의 경우에서 입력값에서 발생한 오류는 지속적으로 축적되어 결과값을 의미없게 만드는 경우가 발생한다. 장단점이 많이 있지만 문제를 해결하기 위한 방법은 다양하다. 유한요소법은 자동차나 송유관과 같은 복잡한 분야에서 상당히 유용하다. 문제의 성격이 변화하거나 요구 정밀도가 바뀔 때라도 쉽게 대처할 수가 있다. 예를 들어, 날씨 예측 시뮬레이션의 경우 면적이 넓은 바다보다 육지에서의 날씨 예측이 중요하며, 이러한 경우 유한요소법이 유용하게 사용될 수 있다.

기술적 논의

여기서는 유한요소법을 2개의 예제를 가지고 나타내도록 하겠다. 이글을 읽는 사람이 미적분학, 선형대수에 익숙하다는 것을 가정하고 기술적 논의를 진행한다.

1차식을 병행한다

${\mbox{P1 }}:{\begin{cases}u''=f{\mbox{ in }}(0,1),\\u(0)=u(1)=0,\end{cases}}$

$f$는 주어진 값이고 $u$는 $x$의 미지함수이다. $u''$는 $x$에 대한 $u$의 2차 미분식이다.

2차식은 디리클레 문제라고도 한다.

${\mbox{P2 }}:{\begin{cases}u_{xx}+u_{yy}=f&{\mbox{ in }}\Omega ,\\u=0&{\mbox{ on }}\partial \Omega ,\end{cases}}$

$\Omega$는 $(x,y)$ 평면에 연결되어 있고 경계부$\partial \Omega$는 괜찮게표현되어 있다. $u_{xx}$와 $u_{yy}$는 각각 $x$와 $y$에 대한 2차 미분을 나타낸다.

P1문제는 부정적분을 계산하여 직접 결과를 얻을 수 있으나 경계조건문제를 풀기위해 부정적분이 통용되는 경우는 고차원 문제로 바뀌지 않는 경우에만 해당된다. 이러한 이유로 인해 P1에서의 유한요소법을 정의하고 그것을 통해 P2의 유한요소법을 정의하겠다.

2개의 단계를 거쳐 설명을 하게 될 것인데, 경계 조건 문제를 유한요소법을 사용하여 해결하도록 하겠다.

1. 첫 번째 단계에서는 기존 BVP를 변분법형태로 바꾼다. 이 단계에서는 계산이 거의 필요없으며 변환형은 수작업도 가능하다.
2. 두 번째 단계는 미분화이다. 두 번째 단계까지 거치고 나면 유한한 범위를 지니는 선형문제를 도출할 수 있고 컴퓨터 계산을 통해 대략적인 값을 알 수 있을 것이다.

변분법 공식화

첫 번째 단계는 P1과 P2를 변분법평형상태로 변환하는 것이다. 만약 $u$가 P1에 대한 해이고, 어떤 smooth function $v$가 변위경계조건을 만족시킨다면 $x=0,1$에서 $v=0$ 이므로 아래의 식을 얻을 수 있다.

(1) $\int _{0}^{1}f(x)v(x)\,dx=\int _{0}^{1}u''(x)v(x)\,dx.$

반대로 주어진 $u$가, (1) 모든 매끄러운 함수 $v(x)$를 만족하면 $u$가 P1의 해가 될 것이다.(소볼레프 공간을 사용하면 증명은 자명하다.)

부분 적분을 사용하여 (1)의 우항을 정리하면 아래의 식을 얻을 수 있다.

(2)${\begin{matrix}\int _{0}^{1}f(x)v(x)\,dx&=&\int _{0}^{1}u''(x)v(x)\,dx\\&=&u'(x)v(x)|_{0}^{1}-\int _{0}^{1}u'(x)v'(x)\,dx\\&=&-\int _{0}^{1}u'(x)v'(x)\,dx=-\phi (u,v).\end{matrix}}$

위 식은 $v(0)=v(1)=0$이라는 것을 전제로 가정한 것이다.

해의 존재성과 유일성의 증명

우리는 $H_{0}^{1}(0,1)$이 $(0,1)$이 $x=0$와 $x=1$에서 $0$ 인 절대 연속 함수라고 정의할 수 있다. 그와 같은 함수는 1회만 미분 가능하며 대칭 구조인 양선형 함수로 볼 수 있다.($\!\,\phi$) 내적을 실시하면 $H_{0}^{1}(0,1)$는 힐베르트 공간으로 변경할 수 있다. (자명하다.) 반대로 좌항 $\int _{0}^{1}f(x)v(x)$역시 내적이며 이경우Lp space $L^{2}(0,1)$에 존재한다. 리스 표현 정리를 힐베르트 공간에 적용시키면 P1에 대한 유일해$u$를 얻을 수 있다.

P2의 변분법

만약 그린 정리를 사용하여 부분적분을 실시하면, 어떠한 $v$에 대해서라도 P2는 $u$라는 해를 가짐을 알 수 있을 것이다.

$\int _{\Omega }fv\,ds=-\int _{\Omega }\nabla u\cdot \nabla v\,ds=-\phi (u,v),$

$\nabla$는 기울기를 의미하고 $\cdot$는 2차원 공간에서의 벡터곱을 의미한다. $\,\!\phi$는 적당한 공간 $H_{0}^{1}(\Omega )$에서 내적할 수 있고 $\Omega$의 1차 미분함수의 값은 0이된다.$\partial \Omega$.

여기서 $v\in H_{0}^{1}(\Omega )$라고 가정하였다. $H_{0}^{1}(\Omega )$공간은 절대 연속 함수로 더이상 정의될 수 없게 된다.(소볼레프 공간을 참조.) 그러므로 존재성과 유일성이 증명되었다.

유한차분법과의 비교

유한차분법(영어: finite difference method, 약자 FDM) 은 유한요소법과 함께 편미분 방정식을 위한 대체 방법이다. 유한요소법과 유한차분법의 차이는 다음과 같다.

• 유한차분법은 미분 방정식에 대해 근사화한다. 반면, 유한요소법은 미분 방정식의 해공간을 근사한다.
• 유한요소법의 가장 매력적인 특징은 복잡한 도형들(그리고 조건들)을 비교적 쉽게 다루는 능력이다. 반면에 유한차분법은 그것의 기본 형식에서 직사각형 모양들과 단순한 교차물(alterations)들을 다루는 것만으로 제한된다. 그러한 이유때문에, 유한요소법에서 도형들을 다루는 것은 이론적으로 간단하다.
• 유한차분법의 가장 매력적인 특징은 사용하기 쉽다는 것이다.

역사

유한요소법은 복잡한 탄성, 구조해석 등의 문제를 해결하기 위해 시작되었다. 초기개발은 알렉산드르 흐렌니코프(러시아어: Хренников) (1941)와 리하르트 쿠란트 (1942)가 시작하였는데, 그들이 접근한 방식은 연속적인 범위를 가지는 문제를 요소망(mesh)라는 세분화된 범위로 나누었다. 흐렌니코프는 범위를 격자로 세분화하였으며 쿠란트는 타원 적분을 위한 편미분 방정식을 유한한 삼각형 영역으로 나누어서 문제해결을 하였다. 쿠란트는 원기둥에서의 뒤틀림 문제를 해결하기 위해 위와 같은 방법을 사용하였다. 유한요소법의 발전은 1950년대 중후반에 시작되었고, 항공기와 구조해석에서 주로 사용되었다. 1960년대에는 도시공학에 사용되었으며 1973년에 출판된 An Analysis of The Finite Element Method에서 물리적 시스템을 수치적으로 모델링하는 응용수학의 한분야로 자리잡게 되었다.

같이 보기

• 유한요소해석
• 무한요소법

외부 링크

• IFER Archived 2020년 7월 20일 - 웨이백 머신 -- Internet Finite Element Resources - an annotated list of FEA links and programs
• Workshop "The Finite Element Method in Biomedical Engineering, Biomechanics and Related Fields" Archived 2006년 7월 17일 - 웨이백 머신
• Finite Element Analysis Resources- Finite Element news, articles and tips
• Finite Element Books- books bibliography
• Mathematics of the Finite Element Method
• Finite Elements Lecture Notes - Lecture notes of the Introduction into Finite Elements course at the Delft University of Technology.
• Finite Element Methods for Partial Differential Equations