육각별
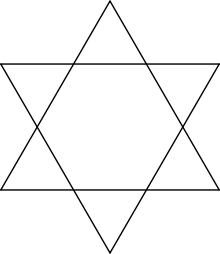
육각성(六角星) 또는 육망성(六芒星), 육각별(六角별), 성형육각형(星型六角形), 육선성형, 헥사그램(Hexagram)은 다각성의 일종으로 6개의 선분이 교차하는 도형이다. 육각형의 각 변을 연장하는 것으로 만들 수 있다. 또, 육각성 중에 있는 육각형을 뽑은 형태를 육광성(六光星)이라 부른다.
유대교가 이 도형을 신성한 것으로 보고 있었다는 근거는 없지만, 17세기 이후부터는 전통적으로 유대인, 유대교를 나타내는 기호로서 정착하고 있다. 이 때문에, 유대인의 나라인 이스라엘의 국기에는 다윗의 별로 불리는 청색의 육각성이 그려져 있다.
등변육각성
[편집]등변육각성은 모든 면이 동일한 육각성이다. 이 도형은 2개의 정삼각형으로 분해할 수 있다. 또, 정n/m각형이라는 방법을 적용하면 6/2, 즉 약분하면 3이 되기 때문에 이 표기법에는 적합하지 않다. 이 다각성은 상기의 2점으로부터 정다각성은 아니게 된다.
육각성의 한붓그리기
[편집]
등변육각성이 정삼각형을 2회로 나누어 그려지는 성질상, 육각성의 한붓그리기는 일견 불가능과 같이 보인다. 하지만, 실제로는 한 편의 정삼각형의 묘화 도중에, 교점에서 한편의 정삼각형의 묘화로 옮겨, 한편의 정삼각형의 묘화가 끝난 시점에서 앞의 정삼각형의 나머지의 부분을 묘화하면 도형 상의 어느 쪽의 위치로부터 시작해도 한붓그리기가 가능하다. 시작점을 교점으로 하면 보다 간단하게 일필 쓰기를 할 수 있다.
교점에서 되풀이하지 않고 한붓그리기가 생기는 육각성도 고안되고 있다. 오른쪽 그림과 같이 정육각형의 정점을 어느 정도 걸러서 날려 묶고, 꼭 알파벳의 'N' (혹은 'Z')을 계속하고 쓰는 육각성이다. 이 육각성은 텔레마에서 자주 이용되는 심볼의 하나이며, 발안자 알레이스터 크롤리의 이름을 씌워 '크로우리의 육각성' 등으로 불린다. 하지만, 목시에서도 확인할 수 있듯이 내각이 등분 불가능하기 때문에, 역시 정다각형은 아니라는 것이 된다.
같이 보기
[편집]- 오각성
- 마겐 다비드 아돔
- 영 파라다이스 - 미야케 유지가 퍼스낼러티를 맡고 있었던 시기에, 같은 프로그램 내에서 '히란야의 수수께끼'라는 코너가 있었다. 육각성 (히란야)이 발한다는 이상한 파워를 청취자가 여러 가지 실험을 하고 엽서로 보고한다는 취지였다. 1985년에는 '이것이 소문의 히란야다 - 피라미드 파워를 넘은 기적의 황금육각성'의 타이틀로 관련책도 출판되었다.
| 이 글은 수학에 관한 토막글입니다. 여러분의 지식으로 알차게 문서를 완성해 갑시다. | |

|
이 글은 종교에 관한 토막글입니다. 여러분의 지식으로 알차게 문서를 완성해 갑시다. |
