이각형
| 정이각형 | |
|---|---|
 | |
| 종류 | 정다각형 |
| 모서리들과 꼭짓점 | 2 |
| 슐레플리 기호 | {2} |
| 콕서터 다이어그램 | |
| 대칭 그룹 | D2, [2], (*2•) |
| 쌍대 다각형 | 자기쌍대 |
기하학에서 이각형은 변과 각이 각각 두개인 다각형을 말한다. 유클리드 기하학에서는 이각형은 두 변이 같거나 둘 중 하나가 휘어야 하기 때문에 축퇴 되었다.
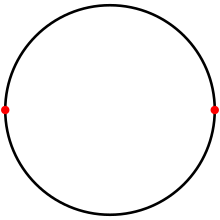
정이각형은 두 각이 같고, 두 변의 길이가 같으며 슐레플리 기호로는 {2}이다. 이것은 구면에서 대척점을 잇는 180°의 현 두개로 이루어져 달꼴으로 만들 수 있다.
이각형은 2 단계의 가장 단순한 추상 폴리토프이다.
깎은 이각형 t{2}는 사각형 {4}이다. 교대된 이각형 h{2}는 일각형 {1}이다.
유클리드 기하학에서[편집]
직선 변을 가지는 이각형은 축퇴되었더라도 정다각형이다. 왜냐하면 두 변의 길이가 같고, 두 각이 (0 도로) 같기 때문이다. 따라서 이각형은 작도 가능한 도형이다.[1]
다각형의 어떤 정의는 유클리드 공간에서 가능하지 않기 때문에 이각형을 적절한 다각형으로 취급하지 않는다.[2]
기본 다면체에서[편집]

이각형을 다면체의 면으로 쓰는 것은 이각형이 축퇴 다각형이기 때문에 축퇴된다. 하지만 종종 이것은 다면체를 변환시킬 때 유용하다.
구면의 달꼴[편집]
이런 이각형으로 이루어진 구면 다면체를 호소헤드론이라 한다.
-
구 위의 달꼴이다.
-
정 육각 호소헤드론의 이각형 여섯개다.
이론에서 중요성[편집]
이각형은 그래프나 다면체의 표면 같은 위상적 네트워크 이론에서 중요한 구성요소이다. 위상적 동등성은 오일러 값과 같은 전역적인 위상적 특성에 영향을 미치지 않고 최소의 다각형 집합으로 줄이는 과정으로 정의할 수 있다. 이각형은 전체 특성에 영향을 주지 않고 간단히 제거하여 선분으로 대체하는 단순화 단계를 나타낼 수 있다.
순환군은 다각형의 회전 대칭으로 얻어질 수 있다: 이각형의 회전 대칭은 C2의 군을 제공한다.


