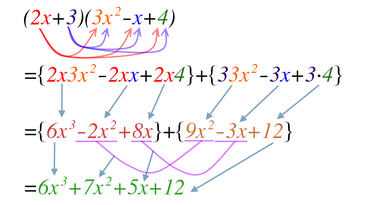
다항식 전개 (多項式 展開, 영어 : polynomial expansion )는 인수 분해 된 다항식 을 인수들끼리 분배법칙 을 이용하여 곱셈을 한 다음, 동류항 들끼리 교환법칙 과 결합법칙 을 이용하여 덧셈뺄셈을 하여 다시 푸는 과정이다. 이렇게 전개된 식을 전개식 (展開式)이라고 한다.
이처럼 다항식의 전개와 인수분해 는 곱셈공식 으로 표현되는 정보교환관계에 있어서 중요한 역할을 한다.
다항식의 덧셈과 뺄셈 [ 편집 ] 다항식의 전개는 분배법칙을 이용하여 분배한 이후, 동류항끼리 계산하여 정리한다. 다항식들의 동류항끼리 덧셈과 뺄셈을 하는 것은 다항식의 연산 의 핵심이다.
예를 들어, 다항식
f
(
x
)
=
2
x
3
−
5
x
+
9
{\displaystyle f(x)=2x^{3}-5x+9}
g
(
x
)
=
x
3
+
2
x
2
+
8
x
−
1
{\displaystyle g(x)=x^{3}+2x^{2}+8x-1}
2
f
(
x
)
−
g
(
x
)
{\displaystyle 2f(x)-g(x)}
=
2
(
2
x
3
−
5
x
+
9
)
−
(
x
3
+
2
x
2
+
8
x
−
1
)
{\displaystyle =2(2x^{3}-5x+9)-(x^{3}+2x^{2}+8x-1)}
=
4
x
3
−
10
x
+
18
−
x
3
+
2
x
2
+
8
x
−
1
{\displaystyle ={4x^{3}-10x+18}-{x^{3}+2x^{2}+8x-1}}
=
3
x
3
−
2
x
2
−
18
x
+
19
{\displaystyle =3x^{3}-2x^{2}-18x+19}
잘 알려진 곱셈 공식 [ 편집 ] 모든 공식에 복부호 동순 이 적용된다.
2차식 [ 편집 ] 좌표평면 에서의 곱셈공식의 의미s
m
(
a
±
b
)
=
m
a
±
m
b
{\displaystyle \,m(a\pm b)=ma\pm mb}
(
a
+
b
)
(
c
+
d
)
=
a
c
+
a
d
+
b
c
+
b
d
{\displaystyle \,(a+b)(c+d)=ac+ad+bc+bd}
(
a
+
b
)
2
=
a
2
+
2
a
b
+
b
2
{\displaystyle \,(a+b)^{2}=a^{2}+2ab+b^{2}}
(
a
−
b
)
2
=
a
2
−
2
a
b
+
b
2
{\displaystyle \,(a-b)^{2}=a^{2}-2ab+b^{2}}
(
a
+
b
)
(
a
−
b
)
=
a
2
−
b
2
{\displaystyle \,(a+b)(a-b)=a^{2}-b^{2}}
(
x
+
a
)
(
x
+
b
)
=
x
2
+
(
a
+
b
)
x
+
a
b
{\displaystyle \,(x+a)(x+b)=x^{2}+(a+b)x+ab}
(
a
x
+
b
)
(
c
x
+
d
)
=
a
c
x
2
+
(
a
d
+
b
c
)
x
+
b
{\displaystyle \,(ax+b)(cx+d)=acx^{2}+(ad+bc)x+b}
(
a
+
b
+
c
)
2
=
a
2
+
b
2
+
c
2
+
2
(
a
b
+
b
c
+
c
a
)
{\displaystyle \,(a+b+c)^{2}=a^{2}+b^{2}+c^{2}+2(ab+bc+ca)}
(
a
x
+
b
y
)
(
c
x
+
d
y
)
=
a
c
x
2
+
(
a
d
+
b
c
)
x
y
+
b
d
y
2
{\displaystyle \,(ax+by)(cx+dy)=acx^{2}+(ad+bc)xy+bdy^{2}}
(
a
x
+
b
y
+
c
)
(
d
x
+
e
y
+
f
)
=
a
d
x
2
+
(
a
f
+
c
d
)
x
+
(
a
e
+
b
d
)
x
y
+
b
e
y
2
+
(
b
f
+
c
e
)
y
+
c
f
{\displaystyle \,(ax+by+c)(dx+ey+f)=adx^{2}+(af+cd)x+(ae+bd)xy+bey^{2}+(bf+ce)y+cf}
아래 2차식들은 곱셈 공식의 변형 의 일부이다.
a
2
+
b
2
+
c
2
−
(
a
b
+
b
c
+
c
a
)
=
a
2
+
b
2
+
c
2
−
a
b
−
b
c
−
c
a
=
1
2
{
(
a
−
b
)
2
+
(
b
−
c
)
2
+
(
c
−
a
)
2
}
{\displaystyle \,a^{2}+b^{2}+c^{2}-(ab+bc+ca)=a^{2}+b^{2}+c^{2}-ab-bc-ca={\frac {1}{2}}\left\{(a-b)^{2}+(b-c)^{2}+(c-a)^{2}\right\}}
(
a
+
b
)
2
=
a
2
+
b
2
+
2
a
b
,
(
a
+
b
)
2
−
2
a
b
=
a
2
+
b
2
{\displaystyle \,(a+b)^{2}=a^{2}+b^{2}+2ab,(a+b)^{2}-2ab=a^{2}+b^{2}}
(
a
−
b
)
2
=
a
2
+
b
2
−
2
a
b
,
(
a
−
b
)
2
+
2
a
b
=
a
2
+
b
2
{\displaystyle \,(a-b)^{2}=a^{2}+b^{2}-2ab,(a-b)^{2}+2ab=a^{2}+b^{2}}
(
a
−
b
)
2
+
2
a
b
=
(
a
+
b
)
2
−
2
a
b
,
(
a
−
b
)
2
+
4
a
b
=
(
a
+
b
)
2
,
(
a
−
b
)
2
=
(
a
+
b
)
2
−
4
a
b
{\displaystyle (a-b)^{2}+2ab=(a+b)^{2}-2ab,(a-b)^{2}+4ab=(a+b)^{2},(a-b)^{2}=(a+b)^{2}-4ab}
3차식 [ 편집 ]
(
x
±
a
)
(
x
±
b
)
(
x
±
c
)
=
x
3
±
(
a
+
b
+
c
)
x
2
+
(
a
b
+
b
c
+
c
a
)
x
±
a
b
c
{\displaystyle \,(x\pm a)(x\pm b)(x\pm c)=x^{3}\pm (a+b+c)x^{2}+(ab+bc+ca)x\pm abc}
(
a
±
b
)
3
=
a
3
±
3
a
2
b
+
3
a
b
2
±
b
3
{\displaystyle \,(a\pm b)^{3}=a^{3}\pm 3a^{2}b+3ab^{2}\pm b^{3}}
(
a
±
b
)
(
a
2
∓
a
b
+
b
2
)
=
a
3
±
b
3
{\displaystyle \,(a\pm b)(a^{2}\mp ab+b^{2})=a^{3}\pm b^{3}}
(
a
+
b
+
c
)
(
a
2
+
b
2
+
c
2
−
a
b
−
b
c
−
c
a
)
=
a
3
+
b
3
+
c
3
−
3
a
b
c
{\displaystyle \,(a+b+c)(a^{2}+b^{2}+c^{2}-ab-bc-ca)=a^{3}+b^{3}+c^{3}-3abc}
1
2
(
a
+
b
+
c
)
{
(
a
−
b
)
2
+
(
b
−
c
)
2
+
(
c
−
a
)
2
}
=
a
3
+
b
3
+
c
3
−
3
a
b
c
{\displaystyle \,{\frac {1}{2}}(a+b+c)\left\{(a-b)^{2}+(b-c)^{2}+(c-a)^{2}\right\}=a^{3}+b^{3}+c^{3}-3abc}
a
3
+
b
3
+
c
3
=
(
a
+
b
+
c
)
(
a
2
+
b
2
+
c
2
−
a
b
−
b
c
−
c
a
)
+
3
a
b
c
{\displaystyle a^{3}+b^{3}+c^{3}=(a+b+c)(a^{2}+b^{2}+c^{2}-ab-bc-ca)+3abc}
4차식 [ 편집 ]
(
a
2
+
a
b
+
b
2
)
(
a
2
−
a
b
+
b
2
)
=
a
4
+
a
2
b
2
+
b
4
{\displaystyle \,(a^{2}+ab+b^{2})(a^{2}-ab+b^{2})=a^{4}+a^{2}b^{2}+b^{4}}
(
a
±
b
)
4
=
a
4
±
4
a
3
b
+
6
a
2
b
2
±
4
a
b
3
+
b
4
{\displaystyle (a\pm b)^{4}=a^{4}\pm 4a^{3}b+6a^{2}b^{2}\pm 4ab^{3}+b^{4}}
(
a
+
b
)
n
{\displaystyle \,(a+b)^{n}}
n
=
{\displaystyle \,n=}
이항 전개 ) 일단 각 항 의 계수 는 생략하였음. 계수 는 파스칼의 삼각형 으로 구한다.
(
a
+
b
)
n
=
a
n
+
a
(
n
−
1
)
b
+
a
(
n
−
2
)
b
2
+
a
(
n
−
3
)
b
3
+
{\displaystyle \,(a+b)^{n}=a^{n}+a^{(n-1)}b+a^{(n-2)}b^{2}+a^{(n-3)}b^{3}+}
+
a
3
b
(
n
−
3
)
+
a
2
b
(
n
−
2
)
+
a
b
(
n
−
1
)
+
b
n
{\displaystyle \,+a^{3}b^{(n-3)}+a^{2}b^{(n-2)}+ab^{(n-1)}+b^{n}}
a
{\displaystyle \,a}
지수 는 점점 작아지고,
b
{\displaystyle \,b}
지수 는 점점 커지며, 전개 한 후에는 모든 항이
n
{\displaystyle \,n}
계수 는 파스칼의 삼각형 을 이용해서 구하는데,
제곱은 3번째 줄, 세제곱은 4번째 줄, 네제곱은 5번째 줄
(
n
{\displaystyle \,(n}
(
n
+
1
)
{\displaystyle \,(n+1)}
)
{\displaystyle )}
계수 로 사용하면 된다.
일반적인 곱셈 공식의 변형 [ 편집 ] 다음은 대한민국 의 2015년 개정 교육과정 에서 쓰이는, 고등학교 1학년 수준의 곱셈 공식의 변형 이다. (단, 2차식 내용의 일부는 중학교 3학년 과정이다.) 모든 공식에 복부호 동순 이 적용된다.
2차식 [ 편집 ]
a
2
+
b
2
=
(
a
±
b
)
2
∓
2
a
b
{\displaystyle \,a^{2}+b^{2}=(a\pm b)^{2}\mp 2ab}
(
a
+
b
)
2
=
(
a
−
b
)
2
+
4
a
b
{\displaystyle \,(a+b)^{2}=(a-b)^{2}+4ab}
x
2
+
1
x
2
=
(
x
±
1
x
)
2
∓
2
{\displaystyle \,x^{2}+{1 \over x^{2}}=\left(x\pm {1 \over x}\right)^{2}\mp 2}
(
x
+
1
x
)
2
−
(
x
−
1
x
)
2
=
4
{\displaystyle \,\left(x+{1 \over x}\right)^{2}-\left(x-{1 \over x}\right)^{2}=4}
a
2
+
b
2
+
c
2
=
(
a
+
b
+
c
)
2
−
2
(
a
b
+
b
c
+
c
a
)
{\displaystyle \,a^{2}+b^{2}+c^{2}=(a+b+c)^{2}-2(ab+bc+ca)}
a
2
+
b
2
+
c
2
±
a
b
±
b
c
±
c
a
=
1
2
{
(
a
±
b
)
2
+
(
b
±
c
)
2
+
(
c
±
a
)
2
}
{\displaystyle \,a^{2}+b^{2}+c^{2}\pm ab\pm bc\pm ca={1 \over 2}\left\{(a\pm b)^{2}+(b\pm c)^{2}+(c\pm a)^{2}\right\}}
3차식 [ 편집 ]
a
3
±
b
3
=
(
a
±
b
)
3
∓
3
a
b
(
a
±
b
)
{\displaystyle \,a^{3}\pm b^{3}=(a\pm b)^{3}\mp 3ab(a\pm b)}
x
3
±
1
x
3
=
(
x
±
1
x
)
3
∓
3
(
x
±
1
x
)
{\displaystyle \,x^{3}\pm {1 \over x^{3}}=\left(x\pm {1 \over x}\right)^{3}\mp 3\left(x\pm {1 \over x}\right)}
a
3
+
b
3
+
c
3
=
(
a
+
b
+
c
)
(
a
2
+
b
2
+
c
2
−
a
b
−
b
c
−
c
a
)
+
3
a
b
c
{\displaystyle \,a^{3}+b^{3}+c^{3}=(a+b+c)(a^{2}+b^{2}+c^{2}-ab-bc-ca)+3abc}
4차식 [ 편집 ]
(
a
2
+
a
b
+
b
2
)
(
a
2
−
a
b
+
b
2
)
=
a
4
+
a
2
b
2
+
b
4
{\displaystyle \,(a^{2}+ab+b^{2})(a^{2}-ab+b^{2})=a^{4}+a^{2}b^{2}+b^{4}}
(
x
2
+
x
+
1
)
(
x
2
−
x
+
1
)
=
x
4
+
x
2
+
1
{\displaystyle \,(x^{2}+x+1)(x^{2}-x+1)=x^{4}+x^{2}+1}
5차식 이상 [ 편집 ]
a
5
+
b
5
=
(
a
2
+
b
2
)
(
a
3
+
b
3
)
−
a
2
b
2
(
a
+
b
)
{\displaystyle \,a^{5}+b^{5}=(a^{2}+b^{2})(a^{3}+b^{3})-a^{2}b^{2}(a+b)}
n
{\displaystyle \,n}
a
n
+
b
n
{\displaystyle \,a^{n}+b^{n}}
k
=
1
2
n
{\displaystyle \,k={1 \over 2}n}
p
=
k
−
0.5
{\displaystyle \,p=k-0.5}
q
=
k
+
0.5
{\displaystyle \,q=k+0.5}
n
{\displaystyle \,n}
a
n
+
b
n
=
(
a
k
+
b
k
)
2
−
2
a
k
b
k
{\displaystyle \,a^{n}+b^{n}=(a^{k}+b^{k})^{2}-2a^{k}b^{k}}
n
{\displaystyle \,n}
a
n
+
b
n
=
(
a
p
+
b
p
)
(
a
q
+
b
q
)
−
a
p
b
p
(
a
+
b
)
{\displaystyle \,a^{n}+b^{n}=(a^{p}+b^{p})(a^{q}+b^{q})-a^{p}b^{p}(a+b)}
같이 보기 [ 편집 ]