z
=
cos
x
+
i
sin
x
{\displaystyle z=\cos x+i\sin x}
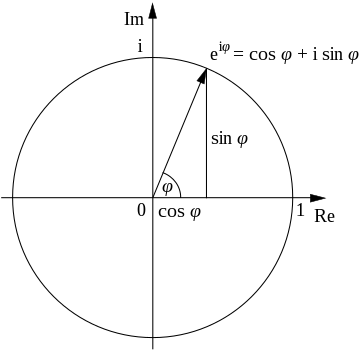
오일러 공식 (Euler's formula)은 수학자 레온하르트 오일러 의 이름이 붙은 공식이다.
사용되는 경우로는 복소수 지수를 정의하는 데에 출발점이 되며, 삼각함수 와 지수함수 에 대한 관계를 나타낸다. 오일러의 등식 은 이 공식의 특수한 경우이다.
오일러 공식은 다음과 같다. 실수
x
{\displaystyle x~}
i
x
{\displaystyle ix~}
e
i
x
=
cos
x
+
i
sin
x
{\displaystyle e^{ix}\,=\,\cos x+i\sin x}
여기서, e 는 자연로그의 밑인 상수이고,
i
{\displaystyle i~}
−
1
{\displaystyle -1~}
i
2
=
−
1
{\displaystyle i^{2}=-1}
허수단위 ,
sin
{\displaystyle \sin }
cos
{\displaystyle \cos }
삼각함수 의 사인과 코사인 함수이다.
x
{\displaystyle x}
π
{\displaystyle \pi }
e
i
π
+
1
=
0
{\displaystyle e^{i\pi }+1=0~}
오일러의 등식 을 구할 수 있다.
오일러 공식은 1714년 로저 코츠 가 다음과 같은 형태로 처음 발견하였다.
ln
(
cos
x
+
i
sin
x
)
=
i
x
{\displaystyle \ln(\cos x+i\sin x)\,=\,ix}
지금과 같은 모양의 오일러 공식은 1748년 오일러가 무한급수 의 좌우 극한값이 같음을 증명하면서 발표되었다. 그러나 로저와 오일러 모두 이 공식이 지닌 '복소수 를 복소평면 위의 하나의 점으로 볼 수 있다'는 기하학적 의미를 눈치채지는 못하였고, 이것은 약 50년이 지난 후에나 발견되었다. 오일러는 현재의 교육과정에서 보다 훨씬 이른 시기에 학생들에게 복소수를 가르쳤다. 그의 기초 대수학 교재인 <대수학 원론 >(Elements of Algebra)에 보면 교재의 거의 맨 앞부분부터 복소수를 도입하고 있고 교재 전체를 통틀어 자연스럽게 사용하고 있다.[1]
발견된 증명 [ 편집 ] 테일러 급수를 이용한 방법 [ 편집 ] 테일러 급수 에 따라 실수 범위에서 다음의 식이 성립한다.
e
x
=
x
0
0
!
+
x
1
1
!
+
x
2
2
!
+
x
3
3
!
+
⋯
=
∑
n
=
0
∞
x
n
n
!
{\displaystyle e^{x}={{x^{0}} \over {0!}}+{{x^{1}} \over {1!}}+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}}
따라서
e
x
=
1
+
x
+
x
2
2
!
+
x
3
3
!
+
⋯
=
∑
n
=
0
∞
x
n
n
!
cos
x
=
1
−
x
2
2
!
+
x
4
4
!
−
x
6
6
!
+
⋯
=
∑
n
=
0
∞
(
−
1
)
n
(
2
n
)
!
x
2
n
sin
x
=
x
−
x
3
3
!
+
x
5
5
!
−
x
7
7
!
+
⋯
=
∑
n
=
0
∞
(
−
1
)
n
(
2
n
+
1
)
!
x
2
n
+
1
{\displaystyle {\begin{array}{rll}e^{x}&{}=1+x+{\frac {x^{2}}{2!}}+{\frac {x^{3}}{3!}}+\cdots &{}=\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}\\\cos x&{}=1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\cdots &{}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n)!}}x^{2n}\\\sin x&{}=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots &{}=\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!}}x^{2n+1}\\\end{array}}}
이때
x
{\displaystyle x}
복소수 일 때에 앞의 무한급수 를 각각의 함수로 정의 한다. 그러면
e
i
z
=
1
+
i
z
+
(
i
z
)
2
2
!
+
(
i
z
)
3
3
!
+
(
i
z
)
4
4
!
+
(
i
z
)
5
5
!
+
(
i
z
)
6
6
!
+
(
i
z
)
7
7
!
+
(
i
z
)
8
8
!
+
⋯
=
1
+
i
z
−
z
2
2
!
−
i
z
3
3
!
+
z
4
4
!
+
i
z
5
5
!
−
z
6
6
!
−
i
z
7
7
!
+
z
8
8
!
+
⋯
=
(
1
−
z
2
2
!
+
z
4
4
!
−
z
6
6
!
+
z
8
8
!
−
⋯
)
+
i
(
z
−
z
3
3
!
+
z
5
5
!
−
z
7
7
!
+
⋯
)
=
cos
z
+
i
sin
z
{\displaystyle {\begin{aligned}e^{iz}&{}=1+iz+{\frac {(iz)^{2}}{2!}}+{\frac {(iz)^{3}}{3!}}+{\frac {(iz)^{4}}{4!}}+{\frac {(iz)^{5}}{5!}}+{\frac {(iz)^{6}}{6!}}+{\frac {(iz)^{7}}{7!}}+{\frac {(iz)^{8}}{8!}}+\cdots \\&{}=1+iz-{\frac {z^{2}}{2!}}-{\frac {iz^{3}}{3!}}+{\frac {z^{4}}{4!}}+{\frac {iz^{5}}{5!}}-{\frac {z^{6}}{6!}}-{\frac {iz^{7}}{7!}}+{\frac {z^{8}}{8!}}+\cdots \\&{}=\left(1-{\frac {z^{2}}{2!}}+{\frac {z^{4}}{4!}}-{\frac {z^{6}}{6!}}+{\frac {z^{8}}{8!}}-\cdots \right)+i\left(z-{\frac {z^{3}}{3!}}+{\frac {z^{5}}{5!}}-{\frac {z^{7}}{7!}}+\cdots \right)\\&{}=\cos z+i\sin z\end{aligned}}}
가 된다.
미분 계산을 이용한 증명방법 [ 편집 ]
f
(
x
)
=
e
−
i
x
(
cos
x
+
i
sin
x
)
⋯
(
1
)
{\displaystyle f(x)=e^{-ix}(\cos x+i\sin x)\cdots (1)}
d
d
x
f
(
x
)
=
−
i
e
−
i
x
(
cos
x
+
i
sin
x
)
+
e
−
i
x
(
−
sin
x
+
i
cos
x
)
=
e
−
i
x
(
−
i
cos
x
+
sin
x
−
sin
x
+
i
cos
x
)
=
0
{\displaystyle {\frac {d}{dx}}f(x)=-ie^{-ix}(\cos x+i\sin x)+e^{-ix}(-\sin x+i\cos x)=e^{-ix}(-i\cos x+\sin x-\sin x+i\cos x)=0}
∴
f
(
x
)
=
C
{\displaystyle \therefore f(x)=C}
C
{\displaystyle C}
(1)에
x
=
0
{\displaystyle x=0}
f
(
0
)
=
1
{\displaystyle f(0)=1}
∴
C
=
1
{\displaystyle \therefore C=1}
e
−
i
x
(
cos
x
+
i
sin
x
)
=
1
{\displaystyle e^{-ix}(\cos x+i\sin x)=1}
e
i
x
=
(
cos
x
+
i
sin
x
)
{\displaystyle e^{ix}=(\cos x+i\sin x)}
Q.E.D.
미적분을 이용한 방법 [ 편집 ] 다음과 같은 복소수
z
{\displaystyle z}
z
=
cos
x
+
i
sin
x
{\displaystyle z=\cos x+i\sin x\,}
양변을
x
{\displaystyle x}
d
z
d
x
=
−
sin
x
+
i
cos
x
{\displaystyle {\frac {dz}{dx}}=-\sin x+i\cos x}
i
2
=
−
1
{\displaystyle i^{2}=-1}
d
z
d
x
=
i
2
sin
x
+
i
cos
x
=
i
(
cos
x
+
i
sin
x
)
=
i
z
{\displaystyle {\frac {dz}{dx}}=i^{2}\sin x+i\cos x=i(\cos x+i\sin x)=iz}
z를 이항한 후 양변을 적분하면:
1
z
d
z
d
x
=
i
∫
1
z
d
z
=
∫
i
d
x
ln
z
=
i
x
+
C
{\displaystyle {\begin{aligned}{\frac {1}{z}}\,{\frac {dz}{dx}}&=i\\\int {\frac {1}{z}}\,dz&=\int i\,dx\\\ln z&=ix+C\end{aligned}}}
(여기에서
C
{\displaystyle C}
이제
C
=
0
{\displaystyle C=0}
x
=
0
{\displaystyle x=0}
ln
z
=
C
z
=
cos
x
+
i
sin
x
=
cos
0
+
i
sin
0
=
1
{\displaystyle {\begin{aligned}\ln z&=C\\z&=\cos x+i\sin x=\cos 0+i\sin 0=1\end{aligned}}}
따라서
ln
1
=
C
C
=
0
{\displaystyle {\begin{aligned}\ln 1&=C\\C&=0\end{aligned}}}
따라서 다음과 같은 식이 성립한다:
ln
z
=
i
x
z
=
e
i
x
e
i
x
=
cos
x
+
i
sin
x
{\displaystyle {\begin{aligned}\ln z&=ix\\z&=e^{ix}\\e^{ix}&=\cos x+i\sin x\end{aligned}}}
Q.E.D.
미분방정식을 이용한 방법 [ 편집 ] 함수
g
(
x
)
{\displaystyle g(x)}
g
(
x
)
=
e
i
x
{\displaystyle g(x)=e^{ix}}
허수단위
i
{\displaystyle i}
g
(
x
)
{\displaystyle g(x)}
도함수 와 이계도함수 는 다음과 같다.
g
′
(
x
)
=
i
e
i
x
g
″
(
x
)
=
i
2
e
i
x
=
−
e
i
x
{\displaystyle {\begin{aligned}g'(x)&=ie^{ix}\\g''(x)&=i^{2}e^{ix}=-e^{ix}\end{aligned}}}
이로부터
g
″
(
x
)
=
−
g
(
x
)
{\displaystyle g''(x)=-g(x)\ }
g
″
(
x
)
+
g
(
x
)
=
0
{\displaystyle g''(x)+g(x)=0\ }
미분방정식 이 만들어지고,일차 독립 인 두 해가 발생한다.
g
1
(
x
)
=
cos
x
g
2
(
x
)
=
sin
x
{\displaystyle {\begin{aligned}g_{1}(x)&=\cos x\\g_{2}(x)&=\sin x\end{aligned}}}
한편, 차수가 같은 미분방정식의 어떤 선형 결합 도 해가 될 수 있으므로 위의 미분방정식의 일반적인 해는 다음과 같다.
g
(
x
)
=
A
g
1
(
x
)
+
B
g
2
(
x
)
=
A
cos
x
+
B
sin
x
g
′
(
x
)
=
−
A
sin
x
+
B
cos
x
{\displaystyle {\begin{aligned}g(x)&=Ag_{1}(x)+Bg_{2}(x)\\&=A\cos x+B\sin x\\g'(x)&=-A\sin x+B\cos x\end{aligned}}}
(
A
{\displaystyle A}
B
{\displaystyle B}
그리고 여기에 함수
g
(
x
)
{\displaystyle g(x)}
g
(
0
)
=
e
i
0
=
1
g
′
(
0
)
=
i
e
i
0
=
i
{\displaystyle {\begin{aligned}g(0)&=e^{i0}&=1\\g'(0)&=ie^{i0}&=i\end{aligned}}}
g
(
0
)
=
−
A
cos
0
+
B
sin
0
=
A
g
′
(
0
)
=
−
A
sin
0
+
B
cos
0
=
B
{\displaystyle {\begin{aligned}g(0)&={\color {White}-}A\cos 0+B\sin 0&=A\\g'(0)&=-A\sin 0+B\cos 0&=B\end{aligned}}}
g
(
0
)
=
A
=
1
g
′
(
0
)
=
B
=
i
{\displaystyle {\begin{aligned}g(0)&=A&=1\\g'(0)&=B&=i\end{aligned}}}
이므로
g
(
x
)
=
e
i
x
=
cos
x
+
i
sin
x
{\displaystyle g(x)\,=\,e^{ix}=\cos x+i\sin x}
Q.E.D.
박사가 사랑한 수식 [ 편집 ] 오일러 공식은 위 소설의 모티브로도 사용이 되었다. 오일러 공식에 숨어 있는 뜻을 cis 함수 또는 복소 지수 함수 는 오일러 공식으로부터 바로 유도되는 함수로, 다음과 같이 정의되는 것이다.
cis
(
θ
)
=
e
i
θ
=
cos
θ
+
i
sin
θ
{\displaystyle \operatorname {cis} (\theta )=e^{i\theta }=\cos \theta +i\sin \theta }
이 함수는 푸리에 변환 이나 페이저 등에서 복소수와 관련된 연산을 할 때 흔히 사용되는 것이다.
쉬운 설명 [ 편집 ] 우선 이 공식을 이해하기 위해서는 멱급수 가 무엇인지 알고 있어야 한다. 멱급수란 하나의 수의 지수를 증가시키며 모두 더한 값을 말하며, 지수함수의 멱급수는 다음과 같다.
e
x
=
1
+
x
+
x
2
2
+
x
3
3
×
2
+
x
4
4
×
3
×
2
+
⋅
⋅
⋅
{\displaystyle e^{x}=1+x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{3\times 2}}+{\frac {x^{4}}{4\times 3\times 2}}+\cdot \cdot \cdot }
이 멱급수의 지수
x
{\displaystyle x}
i
z
{\displaystyle iz}
z
{\displaystyle z}
i
sin
z
{\displaystyle i\sin z}
cos
z
{\displaystyle \cos z}
즉,
e
i
z
=
cos
z
+
i
sin
z
{\displaystyle e^{iz}\,=\,\cos z+i\sin z}
이 등식에서
z
{\displaystyle z}
π
{\displaystyle \pi }
[2]
같이 보기 [ 편집 ]