피라밍크스

피라밍크스 (Pyraminx, /ˈpɪrəmɪŋks/)는 루빅스 큐브 스타일의 정사면체 퍼즐이다. 루비크 에르뇌의 3층 루빅스 큐브 이후 우베 메페르트(Uwe Mèffert)가 만들어 특허를 얻었고, 일본의 다카라토미(세계에서 3번째로 큰 장난감 회사)가 1981년에 세상에 알렸다.[1]
설명[편집]

피라밍크스는 1970년에 메페르트에 의해 처음으로 고안되었다. 그는 1981년에 홍콩으로 가져와 생산하기 전까지는 그의 디자인을 가지고 아무것도 하지 않았다. 우베는 루비크 에르뇌가 그의 큐브를 발명하지 않았으면 피라밍크스는 만들어지지 않았을 것이라고 했다.[출처 필요]
피라밍크스는 정사면체 모양의 4개의 축 조각과, 모서리 조각 6개, 그리고 자명한 꼭짓점이 4개가 있는 퍼즐이다. 이것은 조각의 조합을 맞추기 위해서 틈을 따라서 회전시킬 수 있다. 축 조각은 즉시 명백하게 알 수 있지는 않지만 정팔면체 형태이고, 붙어있는 축을 따라서만 회전할 수 있다. 모서리 조각 6개는 자유롭게 조합을 가질 수 있다. 자명한 꼭짓점은 다른 모든 조각과는 무관하게 돌아가기 때문에 그렇게 부르며, 자명하게 맞는 위치로 옮길 수 있게 만든다. 메페르트는 테트라밍크스라고 불리는 피라밍크스와 다른 모든 것이 같지만 자명한 꼭짓점이 제거되어 깎은 정사면체 형태의 퍼즐을 만들었다.

피라밍크스의 목적은 색을 섞고, 원래의 조합으로 맞추는 것이다.
자명한 꼭짓점 4개는 쉽게 각각 붙어있는 축 조각과 맞출 수 있다; 그리고 축 조각 또한 단순히 돌려서 쉽게 다른 축 조각과 색을 맞출 수 있다. 남은 것은 모서리 조각 6개뿐인데 이것이 이 퍼즐의 진짜 문제이다. 이것은 서로 거울상인 두 4회전 수열을 적용하는 것만으로 풀 수 있다. 이 수열은 한 번에 3개의 모서리 조각의 위치를 조정하고, 그 방향을 다르게 바꾸기 때문에, 두 수열은 퍼즐을 풀기에 충분하다. 하지만, 더 효율적인 솔루션 (더 작은 총 회전수를 요구하는)은 일반적으로 가능하다 (아래를 보라).
각 축 조각의 회전은 꼭짓점의 경우와 같이 나머지 셋과는 무관하다. 여섯개의 모서리 조각은 놓을 수 있는 위치는 6!/2가지이고 뒤집는 것이 홀짝성을 따라서 25가지가 있다. 축 조각의 가능한 위치는 75,582,720가지이기 때문에 이것을 38으로 곱한다. 하지만, 자명한 꼭짓점을 올바른 방향에 놓는 것은 가능한 위치를 테트라밍크스의 방향의 수인 933,120으로 줄인다. 축 조각을 잘 놓는 것은 이것을 11,520으로 줄여서 풀기 더 쉬운 퍼즐로 만든다.
최적 솔루션[편집]
피라밍크스를 풀기 위한 최대 회전 수는 11이다. (자명한 꼭짓점의 회전을 무시하고) 933,120종류의 다른 위치가 있다. 이것은 컴퓨터가 최적 솔루션을 찾기에 충분히 작은 숫자이다. 아래의 표는 피라밍크스를 풀기 위해 n 회전이 필요한 위치의 수 p를 나타낸다[2]:
n 0 1 2 3 4 5 6 7 8 9 10 11 p 1 8 48 288 1728 9896 51808 220111 480467 166276 2457 32
기록[편집]

피라밍크스 해결 세계 최단 기록은 0.75초로, 미국의 Elijah Brown이 2023년 1월 21일에 Berkeley Winter A 2023에서 세웠다. (가장 빠른 것과 느린 것을 제외한) 피라밍크스 해결 다섯 개의 평균의 세계 최단 기록은 1.45초로, 미국의 Ezra Shere가 2023년 9월 23일에 Washtenaw Fast 'n Late Fall 2023.[3]
방법[편집]
피라밍크스를 푸는 방법은 여러가지가 존재하는데, 이것들은 두 그룹으로 나눌 수 있다.
1) V 우선- 이 방법에서, 면이 아니라 둘이나 세 모서리를 먼저 풀고, 나머지 퍼즐을 풀기 위한 LL 알고리즘(last layer 알고리즘)이라 불리는 알고리즘이 주어진다.
2) 상단 우선 방법- 이 방법에서 귀퉁이 주변의 모서리 세 개인 상단의 블록을 먼저 풀고 나머지는 알고리즘으로 해결한다.
일반적인 V 우선 방법-
a) Layer by Layer - 이 방법에서 올바른 위치와 방향에 있는 모든 모서리를 가지는 면(a.k.a. 한 층)을 풀고 나머지 퍼즐은 이 방법을 위해 알고리즘 5개를 사용해서 푼다.
b) L4E- L4E 또는 last 4 edges는 Layer by Layer과 매우 유사하다. 유일한 차이는 세 중심 주변의 두 모서리를 풀고, 나머지는 알고리즘을 통해서 푼다.
c) 직관적 L4E- 많은 시각화가 필요하고 이름이 보여주듯이 L4E와 매우 유사한 방법이다. 이전 방법에 언급된 알고리즘은 기억하지 않는다. 대신에, 큐버들은 직관적으로 각각의 경우에 조각의 움직임을 예상해서 푼다. 이것은 V 우선 방법 중 가장 발전된 방법이다.
일반적인 상단 우선 방법-
a) One Flip- 이 방법은 중앙 주변의 두 모서리를 맞추고 세 번째 모서리를 뒤집히게 둔다. 이 단계 이후에 총 여섯 경우가 있어서 어떤 알고리즘을 기억하고 수행해야 할 지를 결정한다. 세 번째 단계는 Keyhole 마지막 층이라고 불리는 ALL 상단 우선 방법의 일반적인 알고리즘이 사용된다. 여기에는 5개의 알고리즘이 사용되고 그 중 넷은 서로의 거울상이다.
b) Keyhole- 이 방법은 중앙 주변의 두 모서리를 올바른 자리에 놓고, 세 번째 모서리는 모서리의 어떤 색도 맞지 않는다. 즉, 올바른 자리에 있지 않거나 뒤집혀있다. 네 번째 색의 중앙은 이제 맞지 않는 모서리(a.k.a. keyhole)를 이용해서 푼다. 마지막 단계는 마지막 층 알고리즘을 사용해서 푼다.
c) OKA- 이 방법에서, 한 모서리는 잘못된 자리에 있는 두 모서리 주변에 방향이 맞게 있다. 그리고 잘못된 자리에 있는 한 모서리는 스스로를 가로막는 역할을 한다. 마지막 모서리는 바닥층에 있고 이것을 올바른 자리로 두기 위해 매우 간단한 알고리즘을 수행하고, keyhole 마지막 층 알고리즘을 따른다.
다른 일반적인 상단 우선 방법은 WO와 누텔라(Nutella)다.
드류 브래드 같이 피라밍크스 해결 다섯 개의 평균의 세계 최단 기록을 유지하는 프로 피라밍크서들은 보통 모든 방법을 배우고, 경우를 관측할 때 어떤 방법이 그 경우에 적합할 지를 결정한다.[4]
변형[편집]
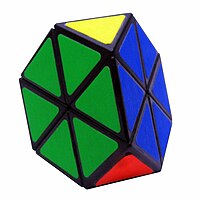
여러 퍼즐의 변형이 있다. 가장 간단한 테트라밍크스는 꼭짓점이 없는 것을 제외하고는 (3x) 피라밍크스와 동일하다 (그림을 보라). 4x 마스터 피라밍크스 (사진을 보라)와 5x 프로페서 피라밍크스와 같이 "높은 차수" 버전의 변형도 존재한다.


마스터 피라밍크스는 (3층과 면마다 9개의 삼각형이 있는 오리지날과 비교하면) 4층이 있고 면마다 16개의 삼각형이 있다. 이 버전은 약 2.17225 × 1017 조합을 가진다.[5][6] 마스터 피라밍크스는 다음을 가지고 있다:
- "꼭짓점" 4개 (오리지날 피라밍크스와 같다)
- "중앙 축" 4개 (오리지날 피라밍크스와 같다)
- "중앙" 4개 (루빅스 큐브와 유사하다, 오리지날 피라밍크스에는 없다)
- "내부 모서리" 6개 (루빅스 큐브와 유사하다, 오리지날 피라밍크스에는 없다)
- "외부 모서리" 12개 (오리지날 피라밍크스의 6개의 2배이다)
요약하면, 마스터 피라밍크스는 30개의 "조작할 수 있는" 조각을 가진다. 하지만, 오리지날과 마찬가지로, 8조각(꼭짓점과 중앙 축)은 위치가 (서로)고정되어있고 그자리에서 회전만 할 수 있다. 또한, 중앙 4개는 그 자리에 고정되어있고 회전만 할 수 있다(루빅스 큐브와 같다). 따라서 18 (30-8-4)개의 "진짜로 움직일 수 있는" 조각이 있다; 이것은 루빅스 큐브의 "진짜로 움직일 수 있는" 조각 20개가의 10% 적기 때문에, 마스터 피라밍크스가 루빅스 큐브(약 4.3252 × 1019[7])보다 200배 적은 조합을 가지는 것은 당연하다.
같이 보기[편집]
각주[편집]
- ↑ “보관된 사본”. 2021년 11월 27일에 원본 문서에서 보존된 문서. 2017년 11월 30일에 확인함.
- ↑ Pyraminx - Jaap's Puzzle Page
- ↑ “Pyraminx - Official World Records (Single and Average)”. 《World Cube Association》. 2023년 10월 4일에 확인함.
- ↑ 세계 큐브 협회 - Drew Brads results.
- ↑ “Full List of Puzzles”. 《gandreas software》. 2016년 4월 28일에 원본 문서에서 보존된 문서. 2016년 12월 31일에 확인함.
- ↑ “Notes on Twisty Puzzles”. Michael Gottlieb. 2016년 12월 31일에 확인함.
- ↑ Martin Schönert "Analyzing Rubik's Cube with GAP": 루빅스 큐브의 순열군은 GAP 컴퓨터 대수학 시스템으로 실험되었다
외부 링크[편집]
- Jaap's Pyraminx and related puzzles page, with solution
- Pyraminx solution from PuzzleSolver
- A solution to the Pyraminx[깨진 링크(과거 내용 찾기)] by Jonathan Bowen
- An efficient and easy to follow solution favoured by speed solvers
- Patterns 피라밍크스의 예쁜 패턴의 콜렉션
