사용자:Respice post te/원주각

The inscribed angle θ circle.

  en:Central angle 2θ

  Inscribed angle θ on en:major arc

  Supplementary inscribed angle θ on minor arc

기하학에서 원주각이란 주어진 호를 제외한 원주 위의 한 점과 호의 양 끝점을 연결하여 얻은 각을 말한다. 원주각의 크기는 같은 호를 가지는 중심각 크기의 절반이다. 원주각 정리는 유클리드 원론 3권의 20번 명제에 나온다.

정리

명제

섬네일|For fixed points A and B, the set of points M in the plane for which the angle ∠AMB is equal to α is an arc of a circle. The measure of ∠AOB, where O is the center of the circle, is 2α.

원주각 정리는 원주각 θ의 크기는 중심각 2θ의 절반이고 같은 중심각을 가지는 모든 원주각의 크기는 같다는 내용의 정리이다.

증명

한 현이 지름인 원주각

섬네일|Case: One chord is a diameter O를 원의 지름이라 하고 원주 위의 두 점 V 와 A를 선택한 후 선 OV이 O를 지나 정반대에 있는 점 B에서 원주와 교차하도록 그린다. 그 후 한 변이 A, B를 지나고 V를 꼭짓점으로 하는 각을 그린.

Draw line OA. Angle ∠BOA is a en:central angle; call it θ. Lines OV and OA are both radii of the circle, so they have equal lengths. Therefore, triangle △VOA is en:isosceles, so angle ∠BVA (the inscribed angle) and angle ∠VAO are equal; let each of them be denoted as ψ.

Angles ∠BOA and ∠AOV add up to 180°, since line VB passing through O is a straight line. Therefore, angle ∠AOV measures 180° − θ.

It is known that the three angles of a 삼각형 add up to 180°, and the three angles of triangle △VOA are:

$$180^{\circ }-\theta ,\quad \phi ,\quad \phi .$$

Therefore,

$$2\psi +180^{\circ }-\theta =180^{\circ }.$$

Subtract

$$(180^{\circ }-\theta )$$

from both sides,

$$2\psi =\theta ,$$

where θ is the central angle subtending arc 틀:Overarc and ψ is the inscribed angle subtending arc 틀:Overarc.

Inscribed angles with the center of the circle in their interior

Case: Center interior to angle

  φ₀ = ∠DVC, θ₀ = ∠DOC

  φ₁ = ∠EVD, θ₁ = ∠EOD

  φ₂ = ∠EVC, θ₂ = ∠EOC

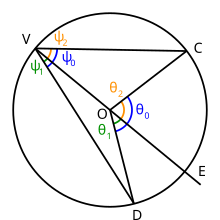
Given a circle whose center is point O, choose three points V, C, D on the circle. Draw lines VC and VD: angle ∠DVC is an inscribed angle. Now draw line OV and extend it past point O so that it intersects the circle at point E. Angle ∠DVC subtends arc 틀:Overarc on the circle.

Suppose this arc includes point E within it. Point E is diametrically opposite to point V. Angles ∠DVE, ∠EVC are also inscribed angles, but both of these angles have one side which passes through the center of the circle, therefore the theorem from the above Part 1 can be applied to them.

Therefore,

$$\angle DVC=\angle DVE+\angle EVC.$$

then let

$${\begin{aligned}\psi _{0}&=\angle DVC,\\\psi _{1}&=\angle DVE,\\\psi _{2}&=\angle EVC,\end{aligned}}$$

so that

$$\psi _{0}=\psi _{1}+\psi _{2}.\qquad \qquad (1)$$

Draw lines OC and OD. Angle ∠DOC is a central angle, but so are angles ∠DOE and ∠EOC, and

$$\angle DOC=\angle DOE+\angle EOC.$$

Let

$${\begin{aligned}\theta _{0}&=\angle DOC,\\\theta _{1}&=\angle DOE,\\\theta _{2}&=\angle EOC,\end{aligned}}$$

so that

$$\theta _{0}=\theta _{1}+\theta _{2}.\qquad \qquad (2)$$

From Part One we know that $\theta _{1}=2\psi _{1}$ and that $\theta _{2}=2\psi _{2}$. Combining these results with equation (2) yields

$$\theta _{0}=2\psi _{1}+2\psi _{2}=2(\psi _{1}+\psi _{2})$$

therefore, by equation (1),

$$\theta _{0}=2\psi _{0}.$$

Inscribed angles with the center of the circle in their exterior

Case: Center exterior to angle

  φ₀ = ∠DVC, θ₀ = ∠DOC

  φ₁ = ∠EVD, θ₁ = ∠EOD

  φ₂ = ∠EVC, θ₂ = ∠EOC

The previous case can be extended to cover the case where the measure of the inscribed angle is the difference between two inscribed angles as discussed in the first part of this proof.

Given a circle whose center is point O, choose three points V, C, D on the circle. Draw lines VC and VD: angle ∠DVC is an inscribed angle. Now draw line OV and extend it past point O so that it intersects the circle at point E. Angle ∠DVC subtends arc 틀:Overarc on the circle.

Suppose this arc does not include point E within it. Point E is diametrically opposite to point V. Angles ∠EVD, ∠EVC are also inscribed angles, but both of these angles have one side which passes through the center of the circle, therefore the theorem from the above Part 1 can be applied to them.

Therefore,

$$\angle DVC=\angle EVC-\angle EVD$$

.

then let

$${\begin{aligned}\psi _{0}&=\angle DVC,\\\psi _{1}&=\angle EVD,\\\psi _{2}&=\angle EVC,\end{aligned}}$$

so that

$$\psi _{0}=\psi _{2}-\psi _{1}.\qquad \qquad (3)$$

Draw lines OC and OD. Angle ∠DOC is a central angle, but so are angles ∠EOD and ∠EOC, and

$$\angle DOC=\angle EOC-\angle EOD.$$

Let

$${\begin{aligned}\theta _{0}&=\angle DOC,\\\theta _{1}&=\angle EOD,\\\theta _{2}&=\angle EOC,\end{aligned}}$$

so that

$$\theta _{0}=\theta _{2}-\theta _{1}.\qquad \qquad (4)$$

From Part One we know that $\theta _{1}=2\psi _{1}$ and that $\theta _{2}=2\psi _{2}$. Combining these results with equation (4) yields

$$\theta _{0}=2\psi _{2}-2\psi _{1}$$

therefore, by equation (3),

$$\theta _{0}=2\psi _{0}.$$

섬네일|400px|Animated gif of proof of the inscribed angle theorem. The large triangle that is inscribed in the circle gets subdivided into three smaller triangles, all of which are isosceles because their upper two sides are radii of the circle. Inside each isosceles triangle the pair of base angles are equal to each other, and are half of 180° minus the apex angle at the circle's center. Adding up these isosceles base angles yields the theorem, namely that the inscribed angle, ψ, is half the central angle, θ.

Corollary

By a similar argument, the angle between a chord and the 접선 line at one of its intersection points equals half of the central angle subtended by the chord. See also en:Tangent lines to circles.

Applications

The inscribed angle 정리 is used in many proofs of elementary en:Euclidean geometry of the plane. A special case of the theorem is en:Thales' theorem, which states that the angle subtended by a 지름 is always 90°, i.e., a right angle. As a consequence of the theorem, opposite angles of 내접 사각형s sum to 180°; conversely, any quadrilateral for which this is true can be inscribed in a circle. As another example, the inscribed angle theorem is the basis for several theorems related to the 방멱 with respect to a circle. Further, it allows one to prove that when two chords intersect in a circle, the products of the lengths of their pieces are equal.

Inscribed angle theorems for ellipses, hyperbolas and parabolas

Inscribed angle theorems exist for ellipses, hyperbolas and parabolas, too. The essential differences are the measurements of an angle. (An angle is considered a pair of intersecting lines.)

• Ellipse
• Hyperbola
• Parabola

References

• Ogilvy, C. S. (1990). 《Excursions in Geometry》. Dover. 17–23쪽. ISBN 0-486-26530-7. 
• Gellert W, Küstner H, Hellwich M, Kästner H (1977). 《The VNR Concise Encyclopedia of Mathematics》. New York: Van Nostrand Reinhold. 172쪽. ISBN 0-442-22646-2. 
• Moise, Edwin E. (1974). 《Elementary Geometry from an Advanced Standpoint》 2판. Reading: Addison-Wesley. 192–197쪽. ISBN 0-201-04793-4. 

External links

• Weisstein, Eric Wolfgang. “Inscribed Angle”. 《Wolfram MathWorld》 (영어). Wolfram Research. 
• Relationship Between Central Angle and Inscribed Angle
• Munching on Inscribed Angles at en:cut-the-knot
• Arc Central Angle With interactive animation
• Arc Peripheral (inscribed) Angle With interactive animation
• Arc Central Angle Theorem With interactive animation
• At bookofproofs.github.io