르장드르 다항식(Legendre polynomial)  는 르장드르 미분 방정식(Legendre differential equation)이라고 불리는 다음 미분 방정식의 해가 되는 함수들이다.
는 르장드르 미분 방정식(Legendre differential equation)이라고 불리는 다음 미분 방정식의 해가 되는 함수들이다.

스튀름-리우빌 형식으로 쓰면,
![{\displaystyle {d \over dx}\left[(1-x^{2}){d \over dx}P(x)\right]+n(n+1)P(x)=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9266eb55b526eba7b39c022c625ed7298a775ad4)
이다. 이 함수와 미분 방정식의 이름은 프랑스의 수학자 아드리앵마리 르장드르의 이름을 따 명명되었다. 이 상미분 방정식은 물리와 공학의 여러 분야에서 자주 등장한다. 특히, 구면좌표계에서 라플라스 방정식을 풀 때 등장한다.
르장드르 다항식[편집]
구체적인 몇몇 르장드르 다항식의 형태는 다음과 같다.

|

|
| 0 |

|
| 1 |

|
| 2
|

|
| 3
|

|
| 4
|

|
| 5
|

|
| 6
|

|
| 7
|

|
| 8
|

|
| 9
|

|
| 10
| 
|
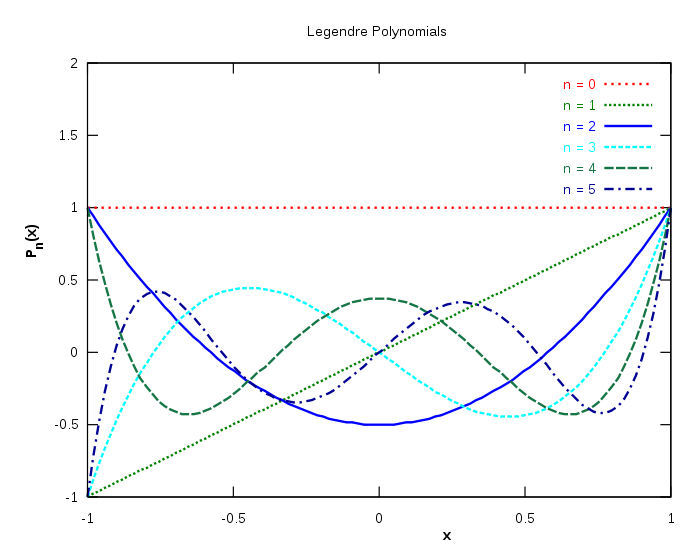
 인 경우의 구간 [-1,1]사이에서의 르장드르 다항식의 그래프는 다음과 같다.
인 경우의 구간 [-1,1]사이에서의 르장드르 다항식의 그래프는 다음과 같다.
간단한 성질[편집]
르장드르 다항식에는 다음과 같은 몇몇 간단한 성질이 있다.




 이 홀수이면
이 홀수이면 
 이 짝수이면
이 짝수이면 
수직 관계[편집]
르장드르 다항식 끼리 구간 [-1,1]에서  내적을 취하면 다음과 같은 결과를 얻는다.
내적을 취하면 다음과 같은 결과를 얻는다.
 .
.
여기서  은 크로네커 델타를 의미한다. 따라서, 르장드르 다항식은 구간 [-1,1]에서 서로 수직함을 알 수 있다. 이는 르장드르 방정식이 스튀름-리우빌 문제에 속하기 때문이다. 즉, 르장드르 미분 방정식을 다음과 같이 스튀름-리우빌 형식으로 놓을 수 있다.
은 크로네커 델타를 의미한다. 따라서, 르장드르 다항식은 구간 [-1,1]에서 서로 수직함을 알 수 있다. 이는 르장드르 방정식이 스튀름-리우빌 문제에 속하기 때문이다. 즉, 르장드르 미분 방정식을 다음과 같이 스튀름-리우빌 형식으로 놓을 수 있다.
![{\displaystyle {d \over dx}\left[(1-x^{2}){d \over dx}P(x)\right]+\lambda P(x)=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d86ba61b9000942e97fdfa5d25bac282bd6aaa6b)
여기서 고윳값  이다. 스튀름-리우빌 문제의 해의 집합은 일반적으로 함수 공간의 정규 직교 기저를 이루므로, 르장드르 다항식도 마찬가지로 직교 기저를 이룬다. (다만, 통상적으로 그 노름이 1이 아니게 정의한다.)
이다. 스튀름-리우빌 문제의 해의 집합은 일반적으로 함수 공간의 정규 직교 기저를 이루므로, 르장드르 다항식도 마찬가지로 직교 기저를 이룬다. (다만, 통상적으로 그 노름이 1이 아니게 정의한다.)
르장드르 다항식의 계산 및 표현[편집]
르장드르 다항식은 점화식이나 선적분, 생성 함수 등 여러 방법으로 표현할 수 있다.
로드리게스 공식[편집]
로드리게스 공식(Rodrigues’ formula)은 르장드르 다항식의 일반식이며, 다음과 같다.
![{\displaystyle P_{n}(x)={1 \over 2^{n}n!}{d^{n} \over dx^{n}}\left[(x^{2}-1)^{n}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9414fbe11099d281205ca2a2f051f405c2d348c)
점화식[편집]
르장드르 다항식은 다음과 같은 점화식을 만족한다.

생성 함수[편집]
르장드르 다항식은 다음과 같은 생성 함수를 가진다.
 .
.
선적분을 통한 표현[편집]
르장드르 다항식은 유수적분을 통해 다음과 같은 적분 형태로 표현될 수 있다.

여기서 적분 경로는 원점을 중심으로 하는 임의의 반시계방향의 폐곡선이다.




![{\displaystyle {d \over dx}\left[(1-x^{2}){d \over dx}P(x)\right]+n(n+1)P(x)=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9266eb55b526eba7b39c022c625ed7298a775ad4)






















![{\displaystyle {d \over dx}\left[(1-x^{2}){d \over dx}P(x)\right]+\lambda P(x)=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d86ba61b9000942e97fdfa5d25bac282bd6aaa6b)

![{\displaystyle P_{n}(x)={1 \over 2^{n}n!}{d^{n} \over dx^{n}}\left[(x^{2}-1)^{n}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9414fbe11099d281205ca2a2f051f405c2d348c)


