싱크로트론 방사
싱크로트론 방사(synchrotron radiation)는 싱크로트론에 의해 생성된 전자기적 방사선이다. 이것은 사이클로트론 방사와 비슷하지만, 자기장에서 빛의 속도에 근접하여 움직이며, 대전된 입자들에 의해 생성된다. 이것은 싱크로트론 또는 스토리지 링(고에너지 하전 입자를 저장하는 장치)에서 인위적으로, 혹은 우주에서 자기장을 통해 빠르게 움직이는 전자에 의해 자연적으로 방사된다. 생성된 방사는 전파부터 적외선, 가시광선, 자외선, 엑스선, 감마선까지 전자기 스펙트럼 전체에 걸쳐 있다.
역사[편집]

싱크로트론 방사는 제너럴 일렉트릭 회사의 싱크로트론 가속기의 발견으로 이름지어졌다. 싱크로트론 가속기는 1946년에 개발되어 1947년 5월 Frank Elder, Anatole Gurewitsch, Robert Langmuir, and Herb Pollock가 쓴 “싱크로트론에서 가속된 전자에서 방출된 방사선”라는 논문에 발표되었다.[1]
4월 24일, 랭뮤어(Robert Langmuir)와 나는 기계를 작동시키고 있었고, 평소처럼 전자총과 그것과 관련된 펄스변성기를 극한으로 보내기위해 노력하였다. 간헐적으로 불꽃이 발생했었고, 우리는 보호용 콘크리트 벽 근처의 거울을 관찰하기 위해 기술자가 필요했다. 그가 시험관에서 arc를 보았을 때 즉시 싱크로트론을 끄라는 신호를 보냈다. 진공상태는 잘 유지 되었고, 랭뮤어와 나는 벽의 끝으로 와서 관찰하였다. 처음에 우리는 이것이 체렌코프 복사 때문이라고 생각했었지만 곧 이바넨코-포메란추크(Ivanenko-Pomeranchuk) 복사를 보는 것임이 더 분명해졌다."[2]
방출 매커니즘[편집]
자기장에 의해 굽은 경로로 움직이게 힘을 받는 전자를 포함하여, 고에너지 입자가 빠른 운동을 할 때, 싱크로트론 방사를 한다. 이것은 전파 안테나와 비슷하나, 이론면에서 차이점이 있다. 로런츠 인자 γ 때문에 상대론적인 속도가 도플러 효과로 측정되는 진동수를 변화시킬 것이다. 자기장 하에서 움직이는 전하를 띈 입자의 운동방정식을 상대론적으로 수식을 기술하면 다음과 같다.
여기서 v는 입자의 속도 벡터이며, q는 입자가 띈 전하, 그리고 B는 자기장 벡터이며, m은 전하의 질량, 마지막으로 는 로렌츠 인자이다. 입자에 가해지는 힘이 입자의 운동에 수직인 방향이라고 하면 자기장은 입자에 일을 하지 않는다. 따라서 입자의 속도는 변하지 않고 일정한 상수로 유지되는 대신 방향만 바뀔 뿐이다. 따라서 위 수식은 다음과 같이 정리할 수 있다.
v 벡터를 B에 수직인 방향과 평행인 방향으로 나누면 다음과 같이 계산할 수 있다.
만약 자기장선에 평행하게 놓인 속도 벡터의 성분이 0이 아니라면, 입자는 나선 경로로 운동한다. 가령 전자가 이러한 운동을 한다고 하면, 전자의 운동에 관한 물리량은 다음과 같이 표현될 수 있다.
여기서 이다.
위쪽에서부터 각각 나선운동의 반지름, 나선운동시 전자의 가속도, 나선운동시 전자 운동의 주기, 나선운동시 전자 운동의 각진동수를 나타낸다. 상대론적인 운동을 하는 전하 q를 띈 입자가 가속도 a로 가속되고 있다면 이로 인해 방출되는 일률은 다음과 같다.
이는 비상대론적인 운동의 경우보다 배 만큼의 수치이다.
상대론적인 시간의 단축은 다른 상수 γ에 의해 실험실에서 관측되는 진동수에 부딪힌다. 그러므로 엑스선 범주로 전자들을 가속시키는 공명하는 구멍의 GeV 진동수를 곱한다. 방사되는 힘은 상대론적 라모 공식에 의해 구할 수 있는 반면, 방출되는 전자의 힘은 아브라함-로런츠-디랙 힘에 의해 구한다. 방사 패턴은 뾰족한 원뿔의 꼭짓점으로 향하는 등방성의 쌍극자 패턴에서 비틀어질 수 있다.
싱크로트론 방사는 엑스선의 가장 밝은 인공의 광원이다. 평면 가속 기하학 구조가 오비탈 평면에서 관찰될 때는 선형 편광된 방사형태가 되고, 평면의 작은 각에서 관찰될 때는 원형 편광된 방사형태가 된다. 한편, 진폭과 진동수는 양극의 식에서 집중된다.
유도[편집]
우선, 리에나르-비헤르트 장에 대한 표현은 다음과 같다.
여기에서
이는 뒤처진 시간의 전하의 위치에서 관찰 지점을 잇는 단위 벡터이며, 는 뒤처진 시간이다.
근접장(near field)의 효과를 무시한다면, 리에나르-비헤르트 장에 의한 포인팅 벡터와 지름 방향 단위벡터 의 내적은 다음과 같다.
- 과 의 공간적인 관계를 통해, 각에 따른 분포의 자세한 정보를 알 수 있다.
- 입자의 정지 틀에서 관찰자의 틀로 변환할 때 상대론적인 효과는 위 식의 분모 에 반영되어 있다.
- 빛의 속도에 가까운 입자에 대해서는 뒤의 효과가 각 분포를 주도한다.
유한한 가속시간 to 동안 단위 입체각에 방사되는 에너지는, 전하의 틀에서 볼 때
이다.
전하가 순간적으로 원운동을 할 때는 가속도 가 속도에 에 직각 방향이다. 순각적인 속도를 z방향으로 잡고 가 x 방향이라 하자. customary polar angles 은 관찰 방향을 결정하며, 식 (4)의 일반적인 형태는 다음의 특수한 형태가 된다
상대론적인 극한에서, 각 분산은 다음과 같이 근사할 수 있다.
분모에 있는 인자 는 각 분산을 마치 자동차 전조등과 같이 입자의 앞에 달린 원뿔 모양으로 집중시킨다. 각 분산 dP/d을 에 대해 그리면 근처에서 날카로운 최댓값을 가진다.
가속기에서의 싱크로트론 방사[편집]
싱크로트론 방사는 가속기에서 입자 물리학 맥락에서 불필요한 에너지 손실을 일으키는 성가신 존재로써 여겨지기도 하고, 또는 많은 실험실에서 사용하기 위해 의도적으로 생산한 방사원으로 사용되기도 한다. 전자들은 GeV 구간에 속한 최종 에너지를 성취하기 위해 몇몇의 단계를 거쳐 빠른 속력으로 가속된다. 또한 대형 강입자 충돌기에서, 양성자 다발은 광전자(7x1010eV까지 진동수와 밀도가 증가하는 파이프 벽에서부터 이차 전자들이 차례차례로 전파된다.)를 전파하면서 진공공간에서 가속되어 진폭과 진동수가 가속될 때 방사된다. 각각의 양성자들은 이러한 현상 때문에 한 회전마다 6.7 keV를 잃게 된다.[3] 기하급수적으로 빛의 속도를 향해 입자를 가속시키는 더 많은 에너지가 소비되기 때문에, 이것은 에너지 보존 법칙에 의해 따르게 된다.
천문학에서의 싱크로트론 방사[편집]

싱크로트론 방사는 천체들에 의해 생성되기도 한다. 기본적으로 자기장을 통해 상대론적인 전자 나선형이 보이며 속도가 변하는 곳에서 생성된다. 싱크로트론 방사의 특징 중 두 가지가 온도가 없는 power-law 스펙트럼과 분극화 현상이다.[4]
그래서 행성들의 입자 충돌과 태양권과 같은 질량의 그룹화에서 감지될 수 있다. 이 방사는 오비탈의 경로에서 평면의 충격이 foreground emission의 최고치를 만들 때 Planck CMB mission을 눈금으로 매기기 위해 유럽 우주국에서 사용된다.[5]
역사[편집]
1956년 제프리 버비지(Geoffrey R. Burbidge가 이를 처녀자리 A 은하에서 분출되는 제트에서 처음 발견하였다.[6], 버비지가 1953년에 슈클로프시키(Iosif S. Shklovskii)에 의해 예측되었던 바를 확인한 것이다. 그러나 사실 1950년에 알페인(Hannes Alfvén)과 Nicolai Herlofson에 의해 몇 년 더 일찍 예측되었다.[7]
T. K. Breus는 천체물리학적 싱크로트론 방사의 역사에서 우선 순위의 의문점이 매우 복잡하다고 아래의 글과 같이 기록하였다.
초대질량 블랙홀이 자기장에서의 대단히 일그러진 관형의 극 지역에서 중력으로 가속되는 이온들에 의해 만들어진 제트의 방출로 인하여 싱크로트론 방사를 만든다고 제안된 바 있다. 제트와 같이, M87에 있는 가장 근접한 제트에서처럼 허블 망원경에 의해 우리의 평면적인 프레임으로부터 빛의 속도보다 빠른 6배의 속도로 움직인다는 것이 명확히 확인되었다. 수많은 비연속적인 설명들이 난무 하였지만 이전의 입자에 관하여 빛의 속도 c로 움직이는 시험관의 입자들 안에 따라다니고, 움직이는 충전된 입자들의 효과의 형식이 모두 '별개의 장 모델(DFM)'과 '아인슈타인 이론'에 의한 것으로 제안되었다. 관찰들은 빛의 속도에 도착하는 관찰에서부터의 빛과 함께 위치의 변화에 관한 것이었다. 그래서 빛의 속도의 불변성(특수 상대성 이론)에 관한 이차적으로 근거로 삼은 것은 침해되지 않았다.
펄사풍성운[편집]
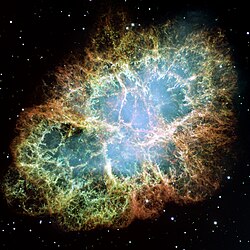
싱크로트론 방출이 중요하게 여겨지는 천문학적인 원천은 펄사풍 성운(Plerion)이다. 게성운이 전형적인 펄사풍 성운이다. 게성운에서 펄사로 방출된 감마선복사는 최근에 25 GeV로 측정되었다.[9] 그 이유는 펄사 근처에서 강한 자기장에 묶인 전자들에 의한 싱크로트론방사 때문이다. 0.1~10MeV의 에너지로 게성운에서의 편광은 기본적으로 싱크로트론 방사를 보여주고 있다.[10]
같이 보기[편집]
각주[편집]
- ↑ Elder, F. R.; Gurewitsch, A. M.; Langmuir, R.V.; Pollock, H.C. (1947). “Radiation from Electrons in a Synchrotron”. 《Physical Review》 71 (11): 829–830.
- ↑ Handbook on Synchrotron Radiation, Volume 1a, Ernst-Eckhard Koch, Ed., North Holland, 1983, reprinted at "Synchrotron Radiation Turns the Big Five-O
- ↑ [1] Synchrotron Radiation Damping in the LHC 2005 Joachim Tuckmantel.
- ↑ Vladimir A. Bordovitsyn, "Synchrotron Radiation in Astrophysics" (1999) Synchrotron Radiation Theory and Its Development Archived 2010년 1월 3일 - 웨이백 머신, ISBN 981-02-3156-3
- ↑ [2] ESA Planck mission, foreground radiation and dust. Images.
- ↑ Burbidge, G. R. “On Synchrotron Radiation from Messier 87”. 《Astrophysical Journal》 124: 416."
- ↑ Alfvén, H.; Herlofson, N. "Cosmic Radiation and Radio Stars" Physical Review (1950), vol. 78, Issue 5, pp. 616–616
- ↑ Breus, T. K., "Istoriya prioritetov sinkhrotronnoj kontseptsii v astronomii %t (Historical problems of the priority questions of the synchrotron concept in astrophysics)" (2001) in Istoriko-Astronomicheskie Issledovaniya, Vyp. 26, p. 88 - 97, 262 (2001)
- ↑ Aliu et al. (The MAGIC collaboration), "Observation of Pulsed {gamma}-Rays Above 25 GeV from the Crab Pulsar with MAGIC", Science 21 November 2008, 322(5905):1221–1224.
- ↑ Dean et al.,"Polarized Gamma-Ray Emission from the Crab", Science 29 August 2008: Vol. 321. no. 5893, pp. 1183–1185
외부 링크[편집]
- Cosmic Magnetobremsstrahlung (synchrotron Radiation), by Ginzburg, V. L., Syrovatskii, S. I., ARAA, 1965
- Developments in the Theory of Synchrotron Radiation and its Reabsorption, by Ginzburg, V. L., Syrovatskii, S. I., ARAA, 1969
- Lightsources.org
- X-Ray Data Booklet













![{\displaystyle \mathbf {B} (\mathbf {r} ,t)=-{\frac {\mu _{0}q}{4\pi }}\left[{\frac {c\,{\hat {\mathbf {n} }}\times {\vec {\beta }}}{\gamma ^{2}R^{2}(1-{\vec {\beta }}\mathbf {\cdot } {\hat {\mathbf {n} }})^{3}}}+{\frac {{\hat {\mathbf {n} }}\times [\,{\dot {\vec {\beta }}}+{\hat {\mathbf {n} }}\times ({\vec {\beta }}\times {\dot {\vec {\beta }}})]}{R\,(1-{\vec {\beta }}\mathbf {\cdot } {\hat {\mathbf {n} }})^{3}}}\right]_{\mathrm {retarded} }\qquad (1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/babf643cc68fb75c6908d4082c15cc6cb47ce27d)
![{\displaystyle \mathbf {E} (\mathbf {r} ,t)={\frac {q}{4\pi \varepsilon _{0}}}\left[{\frac {{\hat {\mathbf {n} }}-{\vec {\beta }}}{\gamma ^{2}R^{2}(1-{\vec {\beta }}\mathbf {\cdot } {\hat {\mathbf {n} }})^{3}}}+{\frac {{\hat {\mathbf {n} }}\times [({\hat {\mathbf {n} }}-{\vec {\beta }})\times {\dot {\vec {\beta }}}\,]}{c\,R\,(1-{\vec {\beta }}\mathbf {\cdot } {\hat {\mathbf {n} }})^{3}}}\right]_{\mathrm {retarded} }\qquad \qquad (2)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f9d4b7231cbf1e2ac2c1e6d285c6325e1c86f64)





![{\displaystyle [\mathbf {S\cdot } {\hat {\mathbf {n} }}]_{\mathrm {retarded} }={\frac {q^{2}}{16\pi ^{2}\varepsilon _{0}c}}\left\{{\frac {1}{R^{2}}}\left|{\frac {{\hat {\mathbf {n} }}\times [({\hat {\mathbf {n} }}-{\vec {\beta }})\times {\dot {\vec {\beta }}}]}{(1-{\vec {\beta }}\mathbf {\cdot } {\hat {\mathbf {n} }})^{3}}}\right|^{2}\right\}_{\mathrm {retarded} }\qquad (3)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/797589765446ad7038cb8190f013d65d54767fd1)





![{\displaystyle {\frac {\mathrm {d} {\mathcal {P}}(t')}{\mathrm {d} {\mathit {\Omega }}}}=R(t')^{2}\,[\mathbf {S} (t')\mathbf {\cdot } {\hat {\mathbf {n} }}(t')]\,{\frac {\mathrm {d} t}{\mathrm {d} t'}}=R(t')^{2}\,\mathbf {S} (t')\mathbf {\cdot } {\hat {\mathbf {n} }}(t')\,[1-{\vec {\beta }}(t')\mathbf {\cdot } {\hat {\mathbf {n} }}(t')]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e32df21b9622215ae2b2c2abfc6261aae44c6399)
![{\displaystyle ={\frac {q^{2}}{16\pi ^{2}\varepsilon _{0}c}}\,{\frac {|{\hat {\mathbf {n} }}(t')\times \{[{\hat {\mathbf {n} }}(t')-{\vec {\beta }}(t')]\times {\dot {\vec {\beta }}}(t')\}|^{2}}{[1-{\vec {\beta }}(t')\mathbf {\cdot } {\vec {\mathbf {n} }}(t')]^{5}}}\qquad \qquad (4)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8af9ab8663b8dfffc38750e62122a74d811ffee6)

![{\displaystyle {\frac {\mathrm {d} {\mathcal {P}}(t')}{\mathrm {d} {\mathit {\Omega }}}}={\frac {q^{2}}{4\pi c^{3}}}{\frac {|{\dot {\mathbf {v} }}|^{2}}{(1-\beta \cos \theta )^{3}}}\left[1-{\frac {\sin ^{2}\theta \cos ^{2}\phi }{\gamma ^{2}(1-\beta \cos \theta )^{2}}}\right]\qquad (5)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2568d2889c17f05c30007143aa65dd7225900d2c)

![{\displaystyle {\frac {\mathrm {d} {\mathcal {P}}(t')}{\mathrm {d} {\mathit {\Omega }}}}\simeq {\frac {2}{\pi }}{\frac {e^{2}}{c^{3}}}\gamma ^{6}{\frac {|{\dot {\mathbf {v} }}|^{2}}{(1+\gamma ^{2}\theta ^{2})^{3}}}\left[1-{\frac {4\gamma ^{2}\theta ^{2}\cos ^{2}\phi }{(1+\gamma ^{2}\theta ^{2})^{2}}}\right]\qquad \qquad (6)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8925788d48dbcf4fe406cbbdb171f58bad5c2d4d)



