헤스의 법칙
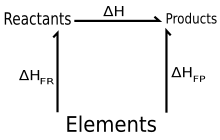
헤스의 법칙(총 열량 불변의 법칙)은 스위스 태생의 러시아 화학자이자 의사인 Germain Hess의 이름을 딴 물리 화학에서의 관계로, 1840년 이것을 발표했다. 이 법칙에 따르면, 화학 반응의 완전한 과정 동안의 엔탈피 변화는 반응이 한 단계에서 또는 여러 단계에서 이루어지는 것과 동일하다. 헤스의 법칙은 열역학 제 1법칙과 화학 공정의 엔탈피가 초기 상태에서 최종 상태로 이동하는 경로와는 무관하다는 사실로 표현되는 에너지 보존 원리의 표현으로 이해된다(즉, 엔탈피는 상태함수이다). 반응 엔탈피 변화는 많은 반응에 대한 열량 측정에 의해 결정될 수 있다. 이 값은 일반적으로 초기 및 최종 온도와 압력이 동일한 조건에 대해 설명되지만 반응 중에 조건이 달라질 수 있다. 헤스의 법칙은 개별적으로 특성화하기 쉬운 합성 단계로 나뉠 수 있는 화학 반응에 필요한 전체 에너지를 결정하는데 사용될 수 있다. 이것은 복잡한 합성을 설계하기 위한 기초로 사용될 수 있는 형성의 표준 엔탈피의 편집을 제공한다.
정의[편집]
헤스의 법칙은 화학 반응(즉, 일정한 압력에서의 반응열)에서 엔탈피의 변화는 초기 상태와 최종 상태 사이의 경로와 무관하다는 것이다. 다른 말로 하면 화학적 변화가 여러 경로로 발생하면 화학적 변화가 일어나는 경로에 관계없이(초기 조건과 최종 조건이 동일하다면) 전체 엔탈피 변화는 동일하다는 것이다. 헤스의 법칙은 반응을 직접 측정할 수 없는 경우에도 엔탈피 변화(ΔH)가 계산될 수 있도록 한다. 이것은 생성 엔탈피에 대해 이전에 결정된 값을 사용하여 화학 반응식을 기반으로 기본 대수 연산을 수행함으로써 수행된다. 화학 방정식을 추가하면 알짜 또는 전체 방정식이 된다. 엔탈피 변화가 각 방정식에 대해 알려진다면 그 결과는 방정식에 대한 엔탈피 변화가 될 것이다. 순 엔탈피 변화가 음의 값(ΔHnet <0)이면, 반응은 발열 반응이며 자발적일 가능성이 높다. 양의 ΔH 값은 흡열 반응에 해당한다. 엔트로피는 또한 자발성을 결정하는 데 중요한 역할을 하지만 양의 엔탈피 변화를 가진 반응은 그럼에도 자발적이다. 헤스의 법칙은 엔탈피 변화가 부가적이라고 말한다. 따라서 단일 반응에 대한 ΔH는
1) 주어진 반응식:
- B2O3 (s) + 3H2O (g) → 3O2 (g) + B2H6 (g) (ΔH = 2035 kJ/mol)
- H2O (l) → H2O (g) (ΔH = 44 kJ/mol)
- H2 (g) + (1/2)O2 (g) → H2O (l) (ΔH = -286 kJ/mol)
- 2B (s) + 3H2 (g) → B2H6 (g) (ΔH = 36 kJ/mol)
다음의 ΔHf를 구하시오:
- 2B (s) + (3/2) O2 (g) → B2O3 (s)
방정식(및 엔탈피 변화)의 곱셈 및 반전 후 결과는 다음과 같다.
- B2H6 (g) + 3O2 (g) → B2O3 (s) + 3H2O (g) (ΔH = -2035 kJ/mol)
- 3H2O (g) → 3H2O (l) (ΔH = -132 kJ/mol)
- 3H2O (l) → 3H2 (g) + (3/2) O2 (g) (ΔH = 858 kJ/mol)
- 2B (s) + 3H2 (g) → B2H6 (g) (ΔH = 36 kJ/mol)
이 방정식을 추가하고 양변에서 공통항을 소거하면:
- 2B (s) + (3/2) O2 (g) → B2O3 (s) (ΔH = -1273 kJ/mol)
2) a) Cgraphite+O2 → CO2 (g) ;(ΔH = -393.5 kJ/mol) (직접 단계)
- b) Cgraphite+1/2 O2 → CO (g) ; (ΔH = -110.5 kJ/mol)
- c) CO (g)+1/2 O2 → CO2 (g); (ΔH = - 283.02 kJ/mol)
→반응 b)와 c)에서 총 ΔH=-393.5KJ/mol. 이는 a)에서 ΔH와 같다.
ΔH 값의 차이는 0.02KJ/mol이며 이는 측정 오류로 인한 것이다.
적용[편집]
헤스의 지속적인 열 합산의 법칙은 다음의 엔탈피를 결정하는데 유용하다:
- 매우 느린 반응에서의 열
- NO(g)와 같은 불안정한 중간체 형성에서의 열
- 위상 전이와 동위 원소 전이의 변화에서의 열
- 음이온을 형성하는 전자 친화력이 알려진 경우 Born-Haber 순환을 구성하여 이온성 물질의 격자에너지 계산
- 이론적인 격자 에너지를 지닌 Born-Harber 순환을 이용한 전자 친화력 계산
같이 보기[편집]
참고 문헌[편집]
더 읽기[편집]
- {{저널 인용| doi = 10.1021/ed028p581 | author = Leicester, Henry M. | title = Germain Henri Hess and the Foundations of Thermochemistry | journal = The Journal of Chemical Education | year = 1951 | volume = 28 | issue = 11 | pages = 581–583 |bibcode = 1951JChEd..28..581L }ㄱ이ㅡㄱㄷ스브7wuuavsnk
외부 링크[편집]
- Hess' paper (1840) on which his law is based (at ChemTeam site)
- a Hess’ Law experiment Archived 2016년 3월 3일 - 웨이백 머신

