산술 시프트
보이기

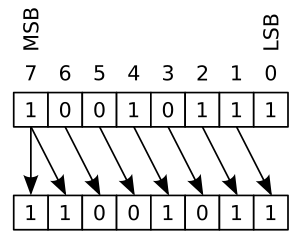
산술 시프트(arithmetic shift)는 연산자 중 하나로서 특수한 2의 거듭제곱수(2, 4, 8, 16 ... 등)와 관련한 곱셈과 나눗셈을 연산할 때 사용된다....
개요[편집]
기호로는 보통 가 사용되며 의 형태로 표시된다. 이 연산의 의미는 컴퓨터의 메모리에 저장된 2진법 숫자를 n비트만큼 좌 또는 우로 이동하라는 의미이며, 한칸마다 2를 곱하거나 나누는 것과 동일한(또는 비슷한) 결과가 나온다. 따라서 이 연산은 다음과 같은 의미를 지닌다
|
|
어떤 메모리 값을 2의 배수 형태의 상수와 곱하거나 나눌 때에는 곱셈/나눗셈 대신에 산술 시프트를 이용할 수 있다. 또한 많은 CPU에서는 상수 곱셈 등의 연산을 시프트 연산자로 처리하는 것이 산술 논리 장치를 거치는 것보다 빠르기 때문에, 컴파일러에서는 곱셈/나눗셈 연산을 자동적으로 산술 시프트 명령어로 변환한다.
논리 시프트와의 차이[편집]
이와 비슷한 연산으로 논리 시프트가 있다. 이 연산 역시 비트를 이동하는 연산이나, 산술 시프트와의 제일 큰 차이는 부호비트(sign bit)가 보존되지 않는다는 것이다. 따라서 부호가 정의된 16비트 정수(signed integer)에서 연산의 결과값이100 0000(2)=32768(10) 이상의 범위를 넘어갈 경우 부호가 바뀌는 경우가 발생한다.
예제[편집]
- (a<<3) + (a<<1) 과 10 * a는 같은 뜻이다.
같이 보기[편집]
참고자료[편집]
- 논리 설계론 관련 서적들
- Computer Architecture 4/E: a Quantitative Approach, Hennessy 지음 (ISBN 981-259-787-5 )




