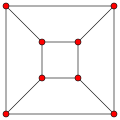
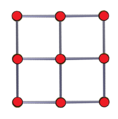
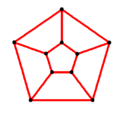
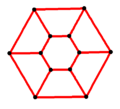
그래프 데카르트 곱의 예. 5개의 꼭짓점 및 5개의 변을 갖는 그래프와 4개의 꼭짓점 및 3개의 변을 갖는 그래프의 데카르트 곱은 5×4=20개의 꼭짓점을 가지며, 5×3+4×5=35개의 변을 가진다. 그래프 데카르트 곱의 예. 5개의 꼭짓점 및 6개의 변을 갖는 그래프와 2개의 꼭짓점 및 1개의 변을 갖는 그래프의 데카르트 곱은 5×2=10개의 꼭짓점을 가지며, 5×1+2×6=17개의 변을 가진다. 그래프 이론 에서 그래프 데카르트 곱 (graph Descartes곱, 영어 : Cartesian product of graphs )은 두 그래프 를 합치는 이항 연산 이다. 이렇게 얻은 그래프의 꼭짓점 의 수는 원래 두 그래프의 꼭짓점의 수들의 곱과 같다.
그래프 의 족
(
Γ
i
)
i
∈
I
{\displaystyle (\Gamma _{i})_{i\in I}}
그래프 데카르트 곱
Γ
=
∏
∐
i
∈
I
Γ
i
{\displaystyle \Gamma ={\prod \!\!\!\!\!\!\!\!}\!\coprod _{i\in I}\Gamma _{i}}
은 다음과 같은 그래프 이다.
V
(
Γ
)
=
∏
i
∈
I
V
(
Γ
i
)
{\displaystyle {\mathsf {V}}(\Gamma )=\prod _{i\in I}{\mathsf {V}}(\Gamma _{i})}
u
v
∈
E
(
Γ
)
⟺
∃
i
∈
I
:
(
u
i
v
i
∈
E
(
Γ
i
)
∧
∀
j
∈
I
∖
{
i
}
:
u
i
=
v
j
)
{\displaystyle uv\in {\mathsf {E}}(\Gamma )\iff \exists i\in I\colon \left(u_{i}v_{i}\in {\mathsf {E}}(\Gamma _{i})\land \forall j\in I\setminus \{i\}\colon u_{i}=v_{j}\right)}
즉, 데카르트 곱
Γ
{\displaystyle \Gamma }
그 꼭짓점
v
∈
V
(
Γ
)
{\displaystyle v\in {\mathsf {V}}(\Gamma )}
Γ
i
{\displaystyle \Gamma _{i}}
(
v
i
)
i
∈
I
{\displaystyle (v_{i})_{i\in I}}
v
i
∈
V
(
Γ
i
)
{\displaystyle v_{i}\in {\mathsf {V}}(\Gamma _{i})}
두 꼭짓점
u
,
v
∈
V
(
Γ
)
{\displaystyle u,v\in {\mathsf {V}}(\Gamma )}
필요 충분 조건 은 어떤 성분
i
∈
I
{\displaystyle i\in I}
u
i
{\displaystyle u_{i}}
v
i
{\displaystyle v_{i}}
그래프
Γ
i
{\displaystyle \Gamma _{i}}
두 그래프
Γ
{\displaystyle \Gamma }
Γ
′
{\displaystyle \Gamma '}
Γ
◻
Γ
′
{\displaystyle \Gamma \,\square \,\Gamma '}
그래프 데카르트 곱은 (표준적 그래프 동형 아래) 결합 법칙 과 교환 법칙 을 따른다. 그래프 데카르트 곱의 항등원 은 한원소 그래프
K
1
{\displaystyle {\mathsf {K}}_{1}}
두 그래프
Γ
{\displaystyle \Gamma }
Γ
′
{\displaystyle \Gamma '}
|
V
(
∏
∐
i
∈
I
Γ
i
)
|
=
∏
i
∈
I
|
V
(
Γ
i
)
|
{\displaystyle \left|{\mathsf {V}}\left({\prod \!\!\!\!\!\!\!\!}\!\coprod _{i\in I}\Gamma _{i}\right)\right|=\prod _{i\in I}|{\mathsf {V}}(\Gamma _{i})|}
|
E
(
∏
∐
i
∈
I
Γ
i
)
|
=
∑
i
∈
I
|
E
(
Γ
i
)
|
∏
j
∈
I
∖
{
i
}
|
V
(
Γ
j
)
|
{\displaystyle \left|{\mathsf {E}}\left({\prod \!\!\!\!\!\!\!\!}\!\coprod _{i\in I}\Gamma _{i}\right)\right|=\sum _{i\in I}|{\mathsf {E}}(\Gamma _{i})|\prod _{j\in I\setminus \{i\}}|{\mathsf {V}}(\Gamma _{j})|}
(무한 그래프의 경우 이는 기수 의 연산으로 해석한다.)
인접 행렬 [ 편집 ] 두 유한 그래프
Γ
{\displaystyle \Gamma }
Γ
′
{\displaystyle \Gamma '}
인접 행렬 은 다음과 같다.
A
Γ
◻
Γ
′
=
A
Γ
⊗
1
V
(
Γ
′
)
+
1
V
(
Γ
)
⊗
A
Γ
′
{\displaystyle {\mathsf {A}}_{\Gamma \,\square \Gamma '}={\mathsf {A}}_{\Gamma }\otimes 1_{{\mathsf {V}}(\Gamma ')}+1_{{\mathsf {V}}(\Gamma )}\otimes {\mathsf {A}}_{\Gamma '}}
여기서
⊗
{\displaystyle \otimes }
크로네커 곱 이다.
특히,
Γ
◻
Γ
′
{\displaystyle \Gamma \,\square \,\Gamma '}
인접 행렬 의 고윳값 의 중복집합 )은
Γ
{\displaystyle \Gamma }
Γ
′
{\displaystyle \Gamma '}
Spec
(
Γ
◻
Γ
′
)
=
Spec
(
Γ
)
+
Spec
(
Γ
′
)
=
{
λ
+
λ
′
:
λ
∈
Spec
Γ
,
λ
′
∈
Spec
Γ
′
}
{\displaystyle \operatorname {Spec} (\Gamma \,\square \,\Gamma ')=\operatorname {Spec} (\Gamma )+\operatorname {Spec} (\Gamma ')=\{\lambda +\lambda '\colon \lambda \in \operatorname {Spec} \Gamma ,\;\lambda '\in \operatorname {Spec} \Gamma '\}}
채색수 [ 편집 ] 유한한 채색수 를 가진, 하나 이상의 꼭짓점을 갖는 두 (유한 또는 무한) 그래프
Γ
{\displaystyle \Gamma }
Γ
′
{\displaystyle \Gamma '}
채색수 는 각 그래프의 채색수 가운데 최댓값 이다. (두 그래프 가운데 하나가 꼭짓점을 갖지 않는다면 그 데카르트 곱의 채색수는 자명하게 0이다.)
χ
(
Γ
◻
Γ
′
)
=
{
max
i
∈
I
{
χ
(
Γ
)
,
χ
(
Γ
′
)
}
(
Γ
≠
∅
≠
Γ
′
)
0
(
∅
∈
{
Γ
,
Γ
′
}
)
{\displaystyle \chi (\Gamma \,\square \,\Gamma ')={\begin{cases}\max _{i\in I}\{\chi (\Gamma ),\chi (\Gamma ')\}&(\Gamma \neq \varnothing \neq \Gamma ')\\0&(\varnothing \in \{\Gamma ,\Gamma '\})\end{cases}}}
증명:
Γ
{\displaystyle \Gamma }
Γ
′
{\displaystyle \Gamma '}
편의상
N
=
max
{
χ
(
Γ
)
,
χ
(
Γ
′
)
}
{\displaystyle N=\max\{\chi (\Gamma ),\chi (\Gamma ')\}}
으로 표기하자. 채색
c
:
V
(
Γ
)
→
Z
/
(
N
)
{\displaystyle c\colon {\mathsf {V}}(\Gamma )\to \mathbb {Z} /(N)}
c
′
:
V
(
Γ
′
)
→
Z
/
(
N
)
{\displaystyle c'\colon {\mathsf {V}}(\Gamma ')\to \mathbb {Z} /(N)}
이 주어졌을 때,
C
:
V
(
Γ
◻
Γ
′
)
→
Z
/
(
N
)
{\displaystyle C\colon {\mathsf {V}}(\Gamma \,\square \,\Gamma ')\to \mathbb {Z} /(N)}
C
:
(
v
,
v
′
)
↦
c
(
v
)
+
c
′
(
v
′
)
{\displaystyle C\colon (v,v')\mapsto c(v)+c'(v')}
는
Γ
◻
Γ
{\displaystyle \Gamma \,\square \,\Gamma }
χ
(
Γ
◻
Γ
′
)
≤
N
{\displaystyle \chi (\Gamma \,\square \,\Gamma ')\leq N}
이다. 그러나
Γ
{\displaystyle \Gamma }
Γ
′
{\displaystyle \Gamma '}
Γ
◻
Γ
′
{\displaystyle \Gamma \,\square \,\Gamma '}
부분 그래프 이다. 따라서
χ
(
Γ
◻
Γ
′
)
≥
N
{\displaystyle \chi (\Gamma \,\square \,\Gamma ')\geq N}
이다.
특히, 두 그래프의 데카르트 곱이 이분 그래프 일 필요 충분 조건 은 다음과 같다.
둘 다 이분 그래프 이거나, 또는 둘 가운데 하나가
∅
{\displaystyle \varnothing }
데카르트 곱 분해 [ 편집 ] 한원소 그래프
K
1
{\displaystyle {\mathsf {K}}_{1}}
데카르트 소 그래프 (Descartes素graph,영어 : Cartesian-prime graph )라고 하자.
모든 연결 유한 그래프 는 소 그래프들의 데카르트 곱으로 표현될 수 있으며, 이러한 표현은 (순서를 무시하면) 유일하다. 그러나 연결 그래프가 아닌 그래프의 경우 이러한 표현은 일반적으로 유일하지 않다. 예를 들어, 다음이 성립한다.
(
K
1
⊔
K
2
⊔
K
2
◻
2
)
◻
(
K
1
⊔
K
2
◻
3
)
=
(
K
1
⊔
K
2
◻
2
⊔
K
2
◻
4
)
◻
(
K
1
⊔
K
2
)
{\displaystyle ({\mathsf {K}}_{1}\sqcup {\mathsf {K}}_{2}\sqcup {\mathsf {K}}_{2}^{\square 2})\,\square \,({\mathsf {K}}_{1}\sqcup {\mathsf {K}}_{2}^{\square 3})=({\mathsf {K}}_{1}\sqcup {\mathsf {K}}_{2}^{\square 2}\sqcup {\mathsf {K}}_{2}^{\square 4})\,\square ({\mathsf {K}}_{1}\sqcup {\mathsf {K}}_{2})}
작은 그래프의 데카르트 곱에 대하여 다음이 성립한다. 여기서
K
i
{\displaystyle {\mathsf {K}}_{i}}
완전 그래프 이며,
K
¯
i
{\displaystyle {\bar {\mathsf {K}}}_{i}}
무변 그래프 이며,
C
i
{\displaystyle {\mathsf {C}}_{i}}
순환 그래프 이며,
P
i
{\displaystyle {\mathsf {P}}_{i}}
경로 그래프 이다.
Γ
{\displaystyle \Gamma }
그래프 이다.
K
1
◻
Γ
=
Γ
{\displaystyle {\mathsf {K}}_{1}\,\square \,\Gamma =\Gamma }
K
2
◻
K
2
=
C
4
{\displaystyle {\mathsf {K}}_{2}\,\square \,{\mathsf {K}}_{2}={\mathsf {C}}_{4}}
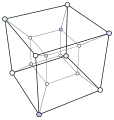
K
2
◻
C
4
=
{\displaystyle {\mathsf {K}}_{2}\,\square \,{\mathsf {C}}_{4}=}
정육면체 그래프
K
¯
i
◻
K
¯
j
=
K
¯
i
j
{\displaystyle {\bar {\mathsf {K}}}_{i}\,\square \,{\bar {\mathsf {K}}}_{j}={\bar {\mathsf {K}}}_{ij}}
K
¯
i
◻
Γ
=
Γ
⊔
i
{\displaystyle {\bar {\mathsf {K}}}_{i}\,\square \,\Gamma =\Gamma ^{\sqcup i}}
K
2
◻
K
2
{\displaystyle {\mathsf {K}}_{2}\,\square \,{\mathsf {K}}_{2}}
K
¯
2
◻
K
¯
3
{\displaystyle {\bar {\mathsf {K}}}_{2}\,\square \,{\bar {\mathsf {K}}}_{3}}
K
¯
3
◻
K
2
{\displaystyle {\bar {\mathsf {K}}}_{3}\,\square \,{\mathsf {K}}_{2}}
K
¯
2
◻
K
3
{\displaystyle {\bar {\mathsf {K}}}_{2}\,\square \,{\mathsf {K}}_{3}}
K
3
◻
K
2
{\displaystyle {\mathsf {K}}_{3}\,\square \,{\mathsf {K}}_{2}}
K
2
◻
K
2
◻
K
2
{\displaystyle {\mathsf {K}}_{2}\,\square \,{\mathsf {K}}_{2}\,\square \,{\mathsf {K}}_{2}}
P
3
◻
P
3
{\displaystyle {\mathsf {P}}_{3}\,\square \,{\mathsf {P}}_{3}}
K
3
◻
K
3
{\displaystyle {\mathsf {K}}_{3}\,\square \,{\mathsf {K}}_{3}}
C
5
◻
K
2
{\displaystyle {\mathsf {C}}_{5}\,\square \,{\mathsf {K}}_{2}}
C
6
◻
K
2
{\displaystyle {\mathsf {C}}_{6}\,\square \,{\mathsf {K}}_{2}}
K
2
◻
K
2
◻
P
3
{\displaystyle {\mathsf {K}}_{2}\,\square \,{\mathsf {K}}_{2}\,\square \,{\mathsf {P}}_{3}}
K
2
◻
K
2
◻
K
3
{\displaystyle {\mathsf {K}}_{2}\,\square \,{\mathsf {K}}_{2}\,\square \,{\mathsf {K}}_{3}}
C
7
◻
K
2
{\displaystyle {\mathsf {C}}_{7}\,\square \,{\mathsf {K}}_{2}}
C
5
◻
K
3
{\displaystyle {\mathsf {C}}_{5}\,\square \,{\mathsf {K}}_{3}}
K
2
◻
K
2
◻
K
2
◻
K
2
{\displaystyle {\mathsf {K}}_{2}\,\square \,{\mathsf {K}}_{2}\,\square \,{\mathsf {K}}_{2}\,\square \,{\mathsf {K}}_{2}}
P
8
◻
K
2
{\displaystyle {\mathsf {P}}_{8}\,\square \,{\mathsf {K}}_{2}}
K
8
◻
K
8
{\displaystyle {\mathsf {K}}_{8}\,\square \,{\mathsf {K}}_{8}}
그래프 데카르트 곱은 1912년에 알프레드 노스 화이트헤드 와 버트런드 러셀 이 《수학 원리 》 2권에서 최초로 사용하였다.[1] 독일어 : Gert Sabidussi , 1929〜)가 1960년에 이 연산을 재발견하였다.[2]
참고 문헌 [ 편집 ] 외부 링크 [ 편집 ]