함수
함수  의 그래프
의 그래프
수학에서, 함수의 그래프(영어: graph)는 정의역의 값과 그에 대한 함수 값을 좌표로 하는 점들로 이루어진 그림이다.
함수  의 그래프는 정의역과 공역의 곱집합의 다음과 같은 부분 집합이다.
의 그래프는 정의역과 공역의 곱집합의 다음과 같은 부분 집합이다.

 차원 실수 벡터의 유클리드 공간의 부분 집합
차원 실수 벡터의 유클리드 공간의 부분 집합  과
과  차원 실수 벡터의 유클리드 공간
차원 실수 벡터의 유클리드 공간  사이의 함수
사이의 함수  의 그래프는
의 그래프는  차원 유클리드 공간
차원 유클리드 공간  의 부분 집합이다. 특히, 함수
의 부분 집합이다. 특히, 함수  의 그래프는 평면 위에서 나타낼 수 있으며, 함수
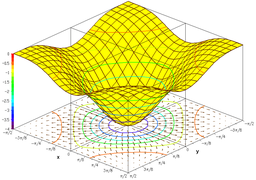
의 그래프는 평면 위에서 나타낼 수 있으며, 함수  의 그래프는 3차원 공간 위에서 나타낼 수 있다.
의 그래프는 3차원 공간 위에서 나타낼 수 있다.
만약  와
와  가 위상 공간이며
가 위상 공간이며  가 연속 함수라면,
가 연속 함수라면,  는
는  매장이며,
매장이며,  는
는  와 위상 동형이다. 만약
와 위상 동형이다. 만약  와
와  가 매끄러운 다양체이며
가 매끄러운 다양체이며  가 매끄러운 함수라면,
가 매끄러운 함수라면,  는
는  매끄러운 매장이며,
매끄러운 매장이며,  는
는  와 미분 동형이다.
와 미분 동형이다.
닫힌집합일 조건[편집]
위상 공간  에 대하여, 다음 두 조건이 서로 동치이다.
에 대하여, 다음 두 조건이 서로 동치이다.
 는 하우스도르프 공간이다.
는 하우스도르프 공간이다.- 임의의 위상 공간
 및 연속 함수
및 연속 함수  에 대하여,
에 대하여,  는 닫힌집합이다.
는 닫힌집합이다.
만약  가 콤팩트 하우스도르프 공간이라면, 위상 공간
가 콤팩트 하우스도르프 공간이라면, 위상 공간  및 함수
및 함수  에 대하여, 다음 두 조건이 서로 동치이다.
에 대하여, 다음 두 조건이 서로 동치이다.
 는 연속 함수이다.
는 연속 함수이다. 는 닫힌집합이다.
는 닫힌집합이다.
-
함수

의 그래프
-
함수

의 그래프
-
함수

의 그래프
-
함수

의 그래프
참고 문헌[편집]
- Jerrold E. Marsden, Anthony J. Tromba (2003). 《Vector Calculus(Fifth Edition)》. W. H. Freeman and Company. ISBN 0-7167-4992-0.
외부 링크[편집]