유카와 퍼텐셜
이 문서의 내용은 출처가 분명하지 않습니다. (2013년 1월) |
유카와 퍼텐셜(Yukawa potential, 가리운 쿨롱 퍼텐셜이라고도 함)은 다음과 같은 형태의 퍼텐셜을 일컫는다.
이 퍼텐셜은 1935년 유카와 히데키에 의해 짧은 거리에서 작용하는 핵력을 설명하기 위해 도입되었다. 유카와는 이러한 퍼텐셜이 질량 인 스칼라 장(예를 들어 파이온 장)의 교환에서 나타난다는 것을 보였다. 이 식에서 장 매개 입자의 질량이 크면 대응하는 힘은 특정 거리(질량에 반비례)까지만 강력하게 작용하고 그 이후로는 무시가능해진다. 반면 질량이 0이면 유카와 퍼텐셜은 쿨롱 퍼텐셜과 같아지고 무한한 거리까지 힘이 작용하게 된다. 유카와는 이러한 이론을 바탕으로 장 매개 입자의 질량이 전자의 200배 정도라고 예측했다.
위 식에서 퍼텐셜은 음수의 값을 갖고, 따라서 대응하는 힘은 인력으로 작용한다. 상수 는 실수값이며, 상호작용하는 메존 장과 페르미온 장 사이의 결합 상수와 같은 값을 갖는다. 핵물리학에서는 이 페르미온으로 양성자나 중성자를 사용한다. 식에서 볼 수 있듯이, 이 퍼텐셜은 중심퍼텐셜이다.
푸리에 변환[편집]
유카와 퍼텐셜이 무거운 장과 연관되어 있음을 이해하는 가장 쉬운 방법은 푸리에 변환을 살펴보는 것이다.
여기서 적분은 3-벡터 모멘텀 의 모든 가능한 값에 대해 수행된다. 이 식에서 는 클라인-고든 방정식의 그린 함수에 해당한다.
파인만 진폭[편집]
유카와 퍼텐셜은 페르미온 쌍의 상호작용에서 최저 차수 진폭만 이용하여 유도할 수 있다. 유카와 상호작용은 페르미온 장 과 메존 장 을 다음 결합 항을 이용해 결합시킨다.
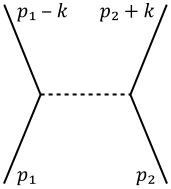
두 페르미온의 산란 진폭은 오른쪽의 파인만 도표를 이용해 주어진다. 이때 한 페르미온의 운동량은 , 다른 페르미온의 운동량은 이라 하며 중간자 교환 운동량은 이다.
파인먼 도형의 규칙에 따라, 각 꼭짓점에 대해 진폭에 만큼의 요소가 곱해진다. 이 도표에 두 개의 꼭짓점이 존재하므로 총 진폭에는 만큼이 곱해져야 한다. 두 페르미온 경로를 연결하는 중앙 직선은 메존의 교환을 의미한다. 입자 교환에 대한 파인먼 규칙은 전파인자를 이용하는 것으로, 무거운 중간자에 대한 전파인자는 이다. 따라서 이 그래프의 파인먼 진폭은 다음과 같음을 알 수 있다.
앞의 절에서 이 식이 유카와 퍼텐셜의 푸리에 변환에 해당한다는 것을 확인할 수 있다.
응집물질 물리학[편집]
유카와 퍼텐셜은 금속 내에 존재하는 불순물의 유효 정전기적 퍼텐셜을 기술하는데도 이용된다. 불순물의 전하 는 금속의 자유전자에 의해 가리워지므로 쿨롱 퍼텐셜을 따르지 않는 대신 유카와 퍼텐셜을 따르게 된다.
충분히 낮은 온도에서는 가 다음의 식을 따른다.
여기서 는 진공의 유전율, 는 전자의 전하량, 는 페르미 준위의 전자 상태 밀도에 해당한다.
강한 전해질 용액이나 플라스마를 이론적으로 다룰 때에도 디바이 차폐의 영향으로 이런 꼴의 퍼텐셜이 등장하는데, 이를 가리켜 디바이-휘켈 퍼텐셜이라 부른다.





















