퀵 정렬
 난수열에 대해 퀵 정렬을 실행한 그림. 수평선은 피벗 값을 가리킨다. | |
| 분류 | 정렬 알고리즘 |
|---|---|
| 자료 구조 | 배열 |
| 최악 시간복잡도 | |
| 최선 시간복잡도 | |
| 평균 시간복잡도 | |
퀵 정렬(Quicksort)은 찰스 앤터니 리처드 호어가 개발한 범용 정렬 알고리즘이다.
다른 원소와의 비교만으로 정렬을 수행하는 비교 정렬에 속한다.
퀵 정렬은 n개의 데이터를 정렬할 때, 최악의 경우에는 O(n2)번의 비교를 수행하고, 평균적으로 O(n log n)번의 비교를 수행한다.
퀵 정렬의 내부 루프는 대부분의 컴퓨터 아키텍처에서 효율적으로 작동하도록 설계되어 있고(그 이유는 메모리 참조가 지역화되어 있기 때문에 CPU 캐시의 히트율이 높아지기 때문이다.), 대부분의 실질적인 데이터를 정렬할 때 제곱 시간이 걸릴 확률이 거의 없도록 알고리즘을 설계하는 것이 가능하다. 또한 매 단계에서 적어도 1개의 원소가 자기 자리를 찾게 되므로 이후 정렬할 개수가 줄어든다. 때문에 일반적인 경우 퀵 정렬은 다른 O(n log n) 알고리즘에 비해 훨씬 빠르게 동작한다. 이러한 이유로 퀵소트(빠른정렬)라는 이름의 기원이 되었다. 그리고 퀵 정렬은 정렬을 위해 평균적으로 O(log n)만큼의 memory를 필요로한다. 이는 재귀적 호출로 발생하는 것이며, 최악의 경우 O(n)의 공간복잡도를 보인다.
원소들 중에 같은 값이 있는 경우 같은 값들의 정렬 이후 순서가 초기 순서와 달라질 수 있어 불안정 정렬에 속한다. 이러한 경우의 C코드 예: 51, 52, 3, 2, 1를 정렬하면 1, 2, 3, 52, 51 이 된다.
알고리즘
[편집]퀵 정렬은 분할 정복(divide and conquer) 방법을 통해 리스트를 정렬한다.
- 리스트 가운데서 하나의 원소를 고른다. 이렇게 고른 원소를 피벗이라고 한다.
- 피벗 앞에는 피벗보다 값이 작은 모든 원소들이 오고, 피벗 뒤에는 피벗보다 값이 큰 모든 원소들이 오도록 피벗을 기준으로 리스트를 둘로 나눈다. 이렇게 리스트를 둘로 나누는 것을 분할이라고 한다. 분할을 마친 뒤에 피벗은 더 이상 움직이지 않는다.
- 분할된 두 개의 작은 리스트에 대해 재귀(Recursion)적으로 이 과정을 반복한다. 재귀는 리스트의 크기가 0이나 1이 될 때까지 반복된다.
재귀 호출이 한번 진행될 때마다 최소한 하나의 원소는 최종적으로 위치가 정해지므로, 이 알고리즘은 반드시 끝난다는 것을 보장할 수 있다.
예제
[편집]퀵정렬의 간단한 설명
퀵정렬은 임의의 pivot 값을 기준으로 pivot 의 좌측에는 pivot 보다 작은값을 두고 우측에는 pivot 보다 큰 값을 두고자 한다.
이 행위는 pivot을 기준으로 좌 우로 이분화 된 리스트를 재귀적으로 반복했을 때 결국 정렬이 완성 된다는 방법 론이다.
보다 쉽게 설명하면 pivot보다 큰 값을 pivot index 보다 왼쪽에서 찾고 ( 큰 값 이 나타날 때까지 i index를 증가시키도록 한다.)
pivot 보다 작은 값을 pivot index 보다 오른쪽에서 찾는다 ( 작은 값이 나타날 때까지 j index를 감소시키도록 한다. )
pivot을 기준으로 값 비교가 완료되었다면 index 결과 i , j를 비교 해본다.
i 값이 j 값 보다 작거나 같다면 분명 pivot 을 기준으로 교환을 해야할 값이 있다는 뜻이 된다.
교환한 뒤 i 인덱스는 증가 j 인덱스는 감소 연산을 수행한다.
i 인덱스가 j 인덱스보다 작거나 같다면 계속 반복해서 수행한다.
위 와 같은 과정은 pivot을 기준으로 왼쪽으로 정렬된 list 에서는 최초 Left 값이 감소된 j 보다 작다면 계속 재귀하면되고,
pivot을 기준으로 오른쪽으로 정렬된 list 에서는 최초 Right 값이 증가된 i 값보다 크다면 계속 재귀하면된다.
피벗은 p, 리스트 왼쪽 끝과 오른쪽 끝에서 시작한 인덱스들을 i,j라고 하자.
5 - 3 - 7 - 6 - 2 - 1 - 4 p
리스트 왼쪽에 있는 i 위치의 값이 피벗 값보다 크고, 오른쪽에 있는 j 위치의 값은 피벗 값보다 작으므로 둘을 교환한다.
5 - 3 - 7 - 6 - 2 - 1 - 4 i j p 1 - 3 - 7 - 6 - 2 - 5 - 4 i j p
j 위치의 값이 피벗 값보다 작지만, i 위치의 값도 피벗값보다 작으므로 교환하지 않는다.
1 - 3 - 7 - 6 - 2 - 5 - 4
i j p
i위치를 피벗 값보다 큰 값이 나올 때까지 진행해 j 위치의 값과 교환한다.
1 - 3 - 7 - 6 - 2 - 5 - 4 i j p 1 - 3 - 2 - 6 - 7 - 5 - 4 i j p
i위치가 j 위치보다 커지면, i 위치의 값과 피벗 값을 교환한다.
1 - 3 - 2 - 6 - 7 - 5 - 4 p 1 - 3 - 2 - 4 - 7 - 5 - 6 p
피벗 값 좌우의 리스트에 대해 각각 퀵 정렬을 재귀적으로 수행한다.
1 - 3 - 2 7 - 5 - 6 1 - 2 - 3 5 - 6 - 7
완성된 리스트는 다음과 같다.
1 - 2 - 3 - 4 - 5 - 6 - 7
정확성 증명
[편집]퀵 정렬 알고리즘은 분할과 정복의 두 단계를 거치므로 정확성도 그 두 단계를 각각 증명한다. 여기서는 분할이 정확함을 보인다. 분할이 정확하다는 뜻을 풀어서 설명하면 다음과 같다.
"임의의 수 x와 배열 형태의 n개의 자료가 주어졌다고 하자. 그 자료에서 x 이상의 값을 가지는 것들 중 최솟값의 자료 이후로 오직 x 이상의 값을 가지는 자료들만을 몰아서 놓을 수 있다."
여기서 참고로, 'x 이상의 값을 가지는 것들'은 수학에서 x의 상계라 하고 'x 이상의 값을 가지는 것들 중 최솟값'은 x의 상한이라고 한다. 그리고 x는 n개의 자료의 값 가운데 있을 필요는 없다. x를 임의의 수로 놓는 이유는 퀵정렬 알고리즘들이 피봇이라는 수를 다양한 방식으로 고를 수 있기 때문이다. 증명 방법은 수학적 강귀납법이다.
- 임의의 수 x와 1개의 자료가 주어지면 그 유일한 자료의 값이 x 미만이거나 이상이다. 미만일 경우는 x 이상의 값을 가지는 것들 자체가 없다는 뜻이므로 주어진 명제는 참이다. 이상일 경우는 x 이상의 값을 가지는 것들이 x뿐이므로 x 이후에 그런 자료들이 놓여 있다.
- k개 이하의 자료가 주어져도 주어진 명제가 성립한다고 가정한다.
- k+1개의 자료가 주어지면 가장 처음 자료의 값이 x 미만이거나 이상이다.
- 미만일 경우, 퀵정렬 알고리즘은 왼쪽 끝 첨수(index)를 1 증가시켜 분할할 자료의 수를 k개로 만든다. 이 k개의 자료는 2번 가정으로 x 이상의 값을 가지는 것들 중 최솟값의 자료 이후로 오직 x 이상의 값을 가지는 자료들만 놓일 것이다. 전체 k+1개 자료 역시 마찬가지다.
- 이상일 경우, 퀵정렬 알고리즘은 자료의 마지막부터 x 미만의 값을 가지는 최초의 자료를 찾아 x 이상인 가장 처음 자료와 자리를 바꾼다. 그래서 분할할 자료는 k-2개 이하로 줄어든다. 2번 가정에 의해 남은 k-2개의 자료는 x 이상인 것과 미만인 것으로 분할되고 전체 k+1개의 자료도 마찬가지다. 만약 마지막부터 x 미만의 값을 가지는 자료가 없다면 이것은 이미 전체 자료가 가장 처음 자료만 x 미만, 그 다음 자료부터는 x 이상으로 분할됐다는 것이다.
자료의 배열이 가지는 원소의 수가 유한하므로 x가 자료 중 하나의 값일 경우, x 이상의 값을 가지는 것들 중 최솟값의 자료는 항상 찾을 수 있다. 퀵 정렬 알고리즘은 분할의 결과로 x 이상의 값을 가지는 것들 중 최솟값의 자료의 배열 상 위치를 함께 표시하여 정렬의 대상에서 제외한다. 그러므로 알고리즘이 무한히 반복되지 않음을 보장한다. 분할한 부분 배열이 정렬되므로 전체 배열이 정렬된다는 것도 수학적 귀납법으로 쉽게 보일 수 있다.
의사 코드와 세부 설명
[편집]
두꺼운 선으로 둘러싸인 원소는 피벗 원소로서, 파티션의 마지막 원소로 한 경우이다.
// 의사 코드임.
function quicksort(q)
var list less, pivotList, greater
if length(q) ≤ 1 then
return q
select a pivot value pivot from q
for each x in q except the pivot element
if x < pivot then add x to less
if x ≥ pivot then add x to greater
add pivot to pivotList
return concatenate(quicksort(less), pivotList, quicksort(greater))
그러나 위 코드는 두 개의 작은 리스트를 저장하기 위해 Ω(n) 크기의 저장공간이 따로 필요하다는 단점이 있다. 실제 구현에서 임시 메모리는 캐시 성능과 속도에 심각한 저하를 가져올 수 있다. 아래와 같이 추가 메모리 없이 배열 내부에서 분할 작업을 구현하면 좀 더 복잡하지만 추가 메모리를 사용하지 않고 구현할 수 있다.
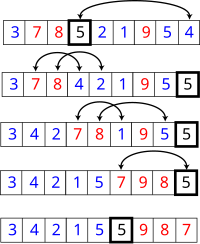
두꺼운 선으로 둘러싸인 원소는 피벗 원소이다. 파란색은 피벗보다 작거나 같고 빨간색은 피벗보다 크다.
function partition(arr, left, right, pivot_index)
pivot_value := arr[pivot_index]
swap(arr[pivot_index], arr[right]) // 피벗을 끝으로 옮겨 놓는다.
stored_index := left
for i in range (left,right) // left에서부터 (right-1)까지
if arr[i] ≤ pivot_value then
swap(arr[stored_index], arr[i])
stored_index := stored_index + 1
swap(arr[right], arr[stored_index]) // 피벗을 두 리스트 사이에 위치시킨다.
return stored_index
이것은 내부 분할 알고리즘이다. 이 알고리즘은 주어진 배열에서 pivot_index에 위치한 값보다 작은 값들을 리스트의 앞쪽에, 큰 값들을 리스트의 맨 뒤에 몰아넣음으로써 left와 right 위치 사이의 원소들을 두 개로 분할한다. 그리고 그렇게 분할된 두 리스트 사이에 피벗을 위치시키면 피벗의 위치가 정해진다. 또한 피벗 값은 임시로 리스트의 맨 뒤에 저장해놓기 때문에 중간에 피벗의 위치가 바뀌거나 하지 않는다.
이렇게 분할 알고리즘을 구현하면 퀵 정렬은 다음과 같이 간단하게 구현할 수 있다.
function quicksort(a, left, right)
if right > left then
select a pivot value for a[pivot_index]
pivot_NewIndex := partition(a, left, right, pivot_index)
quicksort(a, left, pivot_NewIndex-1)
quicksort(a, pivot_NewIndex+1, right)
Pascal과 C와 같은 명령형 언어에서는 대부분 이와 같은 내부 분할을 이용해 구현한다.
개선된 피벗 선택
[편집]퀵 정렬에서 피벗 위치를 결정하는 방법에는 여러 가지 방법이 있다. 기초적인 방법으로는 난수 분할이 사용되는데, 안정성이 떨어진다. 많은 라이브러리에서는 세 값(좌측 끝, 중앙, 우측 끝)의 중위법을 이용하여 분할한다. 이 방법을 사용하면 중앙에서 분할될 가능성이 높아 전체적으로 정렬의 성능이 좋아진다.
복잡도
[편집]의 리스트를 정렬하는데 걸리는 시간을 , 는 임의의 상수라 하고, 리스트가 두 개의 거의같은 부분집합으로 나뉜다고 가정하여 얻은 평균 시간 복잡도는 다음과 같다.
소스 코드
[편집]void quickSort(int arr[], int left, int right) {
int i = left, j = right;
int pivot = arr[(left + right) / 2];
int temp;
while (i <= j)
{
while (arr[i] < pivot) i++; // arr[i] ≥ pivot 일 때까지, left에서 오른쪽 방향으로 탐색
while (arr[j] > pivot) j--; // arr[j] ≤ pivot 일 때까지, right에서 왼쪽 방향으로 탐색
if (i <= j) // 큰 값이 작은 값보다 왼쪽에 있으면
{
// SWAP(arr[i], arr[j])
temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
i++;
j--;
}
}
/* 재귀(recursion) */
if (left < j) quickSort(arr, left, j);
if (i < right) quickSort(arr, i, right);
}
#include <algorithm>//swap
void quickSort(int A[], int low, int high) {
if(low >= high) return; // base condition
// divide process
int i = low, j = low;
int&pivot = A[high];
for (; j < high; ++j) {
if ( A[j] < pivot)
swap(A[i++], A[j]);
}
swap(A[i], pivot);
// conquer process
quickSort(A, low, i-1);
quickSort(A, i+1, high);
}
public void QuickSort(int[] array, int left, int right)
{
if (left >= right) { return; }
int temp;
int pivot = array[(left + right) / 2];
int i = left, j = right;
while (i < j)
{
while (array[i] < pivot) { i++; }
while (pivot < array[j]) { j--; }
if (i < j)
{
if (array[i] == array[j]) { break; }
temp = array[i];
array[i] = array[j];
array[j] = temp;
}
}
QuickSort(array, left, j - 1);
QuickSort(array, j + 1, right);
}
public void quickSort(int[] arr, int left, int right) {
// base condition
if (left >= right) {
return;
}
int pivot = arr[right];
int sortedIndex = left;
for (int i = left; i < right; i++) {
if (arr[i] <= pivot) {
swap(arr, i, sortedIndex);
sortedIndex++;
}
}
swap(arr, sortedIndex, right);
quickSort(arr, left, sortedIndex - 1);
quickSort(arr, sortedIndex + 1, right);
}
private void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
Private Function QR(a() As Long, left As Long, right As Long)
Dim pivot, left_hold, right_hold As Long
left_hold = left
right_hold = right
pivot = a(left)
Do While (left < right)
Do While ((a(right) >= pivot) And (left < right))
right = right - 1
Loop
If left <> right Then
a(left) = a(right)
End If
Do While ((a(left) <= pivot) And (left < right))
left = left + 1
Loop
If left <> right Then
a(right) = a(left)
right = right - 1
End If
Loop
a(left) = pivot
pivot = left
left = left_hold
right = right_hold
If left < pivot Then
Call QR(a(), left, pivot - 1)
End If
If right > pivot Then
Call QR(a(), pivot + 1, right)
End If
End Function
Private Function QS(a() As Long, count As Long)
Call QR(a(), 0, count - 1)
End Function
let rec quicksort = function
| [] -> []
| pivot :: rest ->
let is_less x = x < pivot in
let left, right = List.partition is_less rest in
quicksort left @ [pivot] @ quicksort right
let rec quicksort = function
| [] -> []
| pivot::rest ->
let left, right = rest |> List.partition (fun i -> i < pivot)
quicksort left @ [pivot] @ quicksort right
// Test
printfn "%A" (quicksort [3;5;2;1;4;])
quicksort [] = []
quicksort (p:tl) = quicksort [ x | x <- tl, x <= p ] ++ [p] ++ quicksort [ x | x <- tl, x > p ]
OCaml 과 비교를 쉽게하기 위한 version
quicksort [] = []
quicksort (pivot:rest) =
let left = [x| x <- rest, x <= pivot]
right = [x| x <- rest, x > pivot]
in quicksort left ++ [pivot] ++ quicksort right
def quicksort(x):
if len(x) <= 1:
return x
pivot = x[len(x) // 2]
less = []
more = []
equal = []
for a in x:
if a < pivot:
less.append(a)
elif a > pivot:
more.append(a)
else:
equal.append(a)
return quicksort(less) + equal + quicksort(more)
def partition(arr, start, end):
pivot = arr[start]
left = start + 1
right = end
done = False
while not done:
while left <= right and arr[left] <= pivot:
left += 1
while left <= right and pivot <= arr[right]:
right -= 1
if right < left:
done = True
else:
arr[left], arr[right] = arr[right], arr[left]
arr[start], arr[right] = arr[right], arr[start]
return right
def quick_sort(arr, start, end):
if start < end:
pivot = partition(arr, start, end)
quick_sort(arr, start, pivot - 1)
quick_sort(arr, pivot + 1, end)
return arr
def quickSort(arr:Array[Int]):Array[Int] = {
if (arr.length <= 1) return arr
val pivot = arr(arr.length / 2)
var left, right, equal = Array[Int]()
for (a <- arr) {
if (a < pivot) left = left :+ a
else if (a > pivot) right = right :+ a
else equal = equal :+ a
}
quickSort(left) ++ equal ++ quickSort(right)
}
/**
* 퀵 정렬
* 시간 복잡도: 최악 - O(n2), 최선 - O(nlogn), 평균 - O(nlogn)
* 공간 복잡도: O(1)
* @param {Array} arr
* @param {int} left
* @param {int} right
* @code
var arr = [ 4, 5, 1, 2, 11, 8, 3, 1, 2, 5 ];
quicksort(arr, 0, arr.length-1);
*/
var quicksort = function(arr, left, right) {
if (left < right) {
//기준점을 찾고 기준점을 중심으로 더 작은수, 더 큰수 분류
var i = position(arr, left, right);
//기준점 기준 좌측 정렬
quicksort(arr, left, i - 1);
//기준점 기준 우측 정렬
quicksort(arr, i + 1, right);
}
return arr;
};
var position = function(arr, left, right) {
var i = left;
var j = right;
var pivot = arr[left];
//제자리 더 큰수/더 작은 수 좌우 배치.
while (i < j) {
while (arr[j] > pivot) j--;
while (i < j && arr[i] <= pivot) i++;
tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
arr[left] = arr[j];
arr[j] = pivot;
return j;
}






