오일러 각
오일러 각(Euler角, Euler angle)은 강체가 놓인 방향을 3차원 공간에 표시하기 위해 레온하르트 오일러가 도입한 세 개의 각도이다.[1] 즉, 3차원 회전군 SO(3)의 한 좌표계다. 3차원 공간에 놓인 강체의 방향은 오일러 각도를 사용하여 세 번의 회전을 통해 얻을 수 있다.
정의
[편집]〈그림 1〉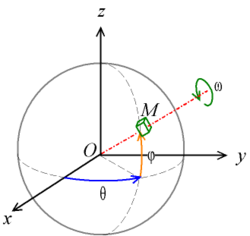
|
〈그림 2〉 |
레온하르트 오일러는 1748년 《무한해석 개론》[2]을 출간하였다. 이 책에서 주로 다루는 것은 무한소의 개념이었으며 오일러 공식과 함께 오일러 각에 대해서도 수록하였다.[3]
오일러 각은 〈그림 1〉과 같이 강체의 방향을 3차원 공간 좌표계의 회전으로 이해하는 것이다. 회전된 좌표계의 각도는 다음과 같이 정의된다.
- 〈그림 2〉와 같이 주어진 3차원 공간 좌표계를 (x, y, z)라고 하고, 이를 회전시킨 좌표계를 (X,Y,Z)라고 하면, 강체의 방향은 다음의 세 각도로 표시될 수 있다.
- α (또는 ψ): z-축(파란색)을 회전축으로 하여 회전된 x-y 좌표축의 각도
- β (또는 θ): 회전된 x-축(즉, N-축, 녹색)을 회전축으로 하여 회전된 z-y 좌표축의 각도
- γ (또는 φ): 위에서 회전된 z-축(즉, Z축, 빨간색)을 회전축으로 하여 회전된 x-y 좌표축의 각도
위와 같이 하여 강체의 방향은 세 개의 각도로 표시될 수 있다. 로봇 제어와 같은 기기 제어에서는 ψ, θ, φ의 표현이 자주 쓰인다.[4] 오일러 각은 강체의 자세를 좌표축의 회전으로 표현하는 여러 방법 가운데 하나로 회전축의 순서에 따라 Z-X-Z 좌표라고도 불린다. 오일러 각 이외에 강체의 자세를 표현하는 방법으로는 좌표계 (X, Y, Z)에 대해 X축 회전을 롤, Y축 회전을 피치, Z축 회전을 요라고 표기하는 X-Y-Z 좌표인 요, 피치, 롤 방식이 있다.[5]
오일러 각의 범위는 α와 γ의 경우 이상적인 상황에서 2π 라디안까지이며, β의 경우 -π/2에서 π/2까지가 된다. β 범위가 제한적인 것을 짐벌 락(영어: gimbal lock)이라 하는데, 이는 앞서 회전한 두 축의 영향으로 세 번째 회전의 가동 범위가 줄어들기 때문이다. 아폴로 11호의 경우 짐벌 락 때문에 자세 제어에 어려움이 있었다.[6]
같이 보기
[편집]각주
[편집]- ↑ 기전연구사, 자동기계기구학, 2008, ISBN 90-70-03333-0 {{isbn}}의 변수 오류: 유효하지 않은 ISBN., 310쪽.
- ↑ L. Euler, Introductio in analysin infinitorum (무한 해석 개론), 1748. 영역 J. D. Blanton (1988), Introduction to analysis of the infinite, Springer, ISBN 978-0-387-96824-7
- ↑ 모리 쓰요시, 김경은 역, 불완전한 천재 수학자들, 살림MATH, 2008, ISBN 89-522-0979-6, 110쪽.
- ↑ 김진호, 기초로봇공학, 성안당, 1999, ISBN 89-315-0291-5, 135-136쪽.
- ↑ 이징구 외, 정밀측정공학, 기전연구사, 2002, ISBN 89-336-0594-0, 553쪽.
- ↑ Gimbal Angles, Gimbal Lock, and a Fourth Gimbal for Christmas Archived 2009년 5월 29일 - 웨이백 머신, 미항공우주국 홈페이지.
| 이 글은 기하학에 관한 토막글입니다. 여러분의 지식으로 알차게 문서를 완성해 갑시다. |
