레일리 분포
확률 밀도 함수
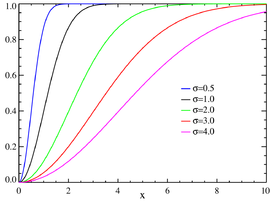
누적 분포 함수
매개변수
σ
>
0
{\displaystyle \sigma >0\,}
지지집합
x
∈
[
0
;
∞
)
{\displaystyle x\in [0;\infty )}
확률 밀도
x
exp
(
−
x
2
2
σ
2
)
σ
2
{\displaystyle {\frac {x\exp \left({\frac {-x^{2}}{2\sigma ^{2}}}\right)}{\sigma ^{2}}}}
누적 분포
1
−
exp
(
−
x
2
2
σ
2
)
{\displaystyle 1-\exp \left({\frac {-x^{2}}{2\sigma ^{2}}}\right)}
기댓값
σ
π
2
{\displaystyle \sigma {\sqrt {\frac {\pi }{2}}}}
중앙값
σ
ln
(
4
)
{\displaystyle \sigma {\sqrt {\ln(4)}}\,}
최빈값
σ
{\displaystyle \sigma \,}
분산
4
−
π
2
σ
2
{\displaystyle {\frac {4-\pi }{2}}\sigma ^{2}}
비대칭도
2
π
(
π
−
3
)
(
4
−
π
)
3
/
2
{\displaystyle {\frac {2{\sqrt {\pi }}(\pi -3)}{(4-\pi )^{3/2}}}}
첨도
−
6
π
2
−
24
π
+
16
(
4
−
π
)
2
{\displaystyle -{\frac {6\pi ^{2}-24\pi +16}{(4-\pi )^{2}}}}
엔트로피
1
+
ln
(
1
2
σ
3
)
+
γ
2
{\displaystyle 1+\ln \left({\frac {1}{{\sqrt {2}}\sigma ^{3}}}\right)+{\frac {\gamma }{2}}}
적률생성함수
1
+
σ
t
e
σ
2
t
2
/
2
π
2
(
erf
(
σ
t
2
)
+
1
)
{\displaystyle 1+\sigma t\,e^{\sigma ^{2}t^{2}/2}{\sqrt {\frac {\pi }{2}}}\left({\textrm {erf}}\left({\frac {\sigma t}{\sqrt {2}}}\right)\!+\!1\right)}
레일리 분포 (Rayleigh distribution)는 확률론 과 통계학 에서 연속 확률 분포 의 한 종류이다. 흔히 2차원 벡터의 직교 성분이 정규 분포 일 경우, 벡터의 크기는 레일리 분포를 갖는다. 예를 들어 바람을 2차원 벡터로 나타냈을 때, 벡터의 두 직교 성분이 정규 분포이면, 바람의 속력은 레일리 분포를 따른다. 실수부와 허수부가 독립적으로 정규 분포를 따르는 복소수 가 있다면, 복소수의 절댓값이 레일리 분포를 나타낸다.
레일리 분포의 확률 밀도 함수는 다음과 같다.
f
(
x
|
σ
)
=
x
exp
(
−
x
2
2
σ
2
)
σ
2
{\displaystyle f(x|\sigma )={\frac {x\exp \left({\frac {-x^{2}}{2\sigma ^{2}}}\right)}{\sigma ^{2}}}}
erfi
(
z
)
{\displaystyle {\textrm {erfi}}(z)\ }
오차 함수 라고 할 때, 특성 함수 는 다음과 같다.
φ
(
t
)
=
{\displaystyle \varphi (t)=}
1
−
σ
t
e
−
σ
2
t
2
/
2
π
2
(
erfi
(
σ
t
2
)
−
i
)
{\displaystyle 1\!-\!\sigma te^{-\sigma ^{2}t^{2}/2}{\sqrt {\frac {\pi }{2}}}\!\left({\textrm {erfi}}\!\left({\frac {\sigma t}{\sqrt {2}}}\right)\!-\!i\right)}
erf
(
z
)
{\displaystyle {\textrm {erf}}(z)\ }
오차 함수 일 때, 모멘트생성 함수 는 다음과 같다.
M
(
t
)
=
{\displaystyle M(t)=\,}
1
+
σ
t
e
σ
2
t
2
/
2
π
2
(
erf
(
σ
t
2
)
+
1
)
{\displaystyle 1+\sigma t\,e^{\sigma ^{2}t^{2}/2}{\sqrt {\frac {\pi }{2}}}\left({\textrm {erf}}\left({\frac {\sigma t}{\sqrt {2}}}\right)\!+\!1\right)}
Γ
(
z
)
{\displaystyle \Gamma (z)}
감마 함수 일 때, 원적률 은 다음과 같다.
μ
k
=
σ
k
2
k
/
2
Γ
(
1
+
k
/
2
)
{\displaystyle \mu _{k}=\sigma ^{k}2^{k/2}\,\Gamma (1+k/2)\,}
모멘트를 이용하면 평균, 분산 , 왜도, 첨도 등을 구할 수 있다.
모수 추정 [ 편집 ]
σ
{\displaystyle \sigma }
최대우도 추정공식은 다음과 같다.
σ
≈
1
2
N
∑
i
=
0
N
x
i
2
{\displaystyle \sigma \approx {\sqrt {{\frac {1}{2N}}\sum _{i=0}^{N}x_{i}^{2}}}}
다른 확률 분포 [ 편집 ]
X
∼
N
(
0
,
σ
2
)
{\displaystyle X\sim N(0,\sigma ^{2})}
Y
∼
N
(
0
,
σ
2
)
{\displaystyle Y\sim N(0,\sigma ^{2})}
정규 분포 일 때
R
=
X
2
+
Y
2
{\displaystyle R={\sqrt {X^{2}+Y^{2}}}}
R
∼
R
a
y
l
e
i
g
h
(
σ
)
{\displaystyle R\sim \mathrm {Rayleigh} (\sigma )}
R
∼
R
a
y
l
e
i
g
h
(
1
)
{\displaystyle R\sim \mathrm {Rayleigh} (1)}
R
2
{\displaystyle R^{2}}
자유도 가 2인 카이 제곱 분포 이다.
R
2
∼
χ
2
2
{\displaystyle R^{2}\sim \chi _{2}^{2}}
X
{\displaystyle X}
지수 분포
X
∼
E
x
p
o
n
e
n
t
i
a
l
(
x
|
λ
)
{\displaystyle X\sim \mathrm {Exponential} (x|\lambda )}
Y
=
2
X
σ
λ
∼
R
a
y
l
e
i
g
h
(
y
|
σ
)
{\displaystyle Y={\sqrt {2X\sigma \lambda }}\sim \mathrm {Rayleigh} (y|\sigma )}
카이 분포 는 레일리 분포를 일반화한 것이다.라이스 분포 는 레일리 분포를 일반화 한 것이다.베이불 분포 는 레일리 분포를 일반화한 것이다.같이 보기 [ 편집 ]