질량 중심
질량 중심(質量中心)은 물체 전체의 질량의 중심점으로, 전체 질량이 질량 중심에 있는 것처럼 외부 계와 작용한다.
미분 질량의 위치를 질량가중치(미분질량/전체질량)를 곱하여 적분한 것이다. 중력이 균일한 경우 무게 중심과 같으므로, 혼용되어 쓰이기도 한다. 이때는 물체의 각 부분에 작용하는 중력을 합한 합력의 작용점을 무게 중심이라고 한다.
정의[편집]
입자계의 질량의 중심 은 위치계 위치 의 평균으로 정의된다.:
질량 밀도 또, 도형 D와 그 주변의 각 점 x가 밀도 f(x)를 가질 경우, 그 중심 g는
를 채우는 점 g이다. 물론 g가 D 밖의 점일 수도 있다.
다각형, 다면체의 무게 중심[편집]
다각형, 다면체에서의 (일반화된)중심[편집]
다각형, 다면체에서의 중심이란, 그 도형의 중력의 합력의 작용점을 지칭한다.
도형의 무게 중심[편집]
중력에 의한 알짜 토크가 0인 점으로 삼각형(다른 도형의 무게 중심 구하는 방법은 아래 그림 참고)의 경우 중선은 한 점에서 만나는데(증명은 삼각형의 닮음 또는 체바 정리 등을 이용하면 쉽게 해결됨), 이 점이 바로 다각형과 다면체의 질량 중심이라 한다. 특히 삼각형의 경우 세 중선의 교점으로, 한 중선을 2:1로 내분하는 점이다.
 |
 |
삼각형의 중선과 무게중심
|
사각형의 중선과 무게중심
|
임의의 2차원 물리 형태의 중심 질량[편집]
이 방식은 알 수 없는 크기의 복잡한 평면 물체의 중력 중심을 찾아내려고 할 때 유용하다.
 |
 |
 |
| 1 단계: 임의의 2차원 모형. | 2 단계: 다림줄을 놓고 그 위치에 O 표한다. | 3 단계: 다림줄을 다시 놓고 O 표한다. 두 선의 교점이 중력의 중심이다. |
애니메이션[편집]
천체역학에서 두 개의 구상 전체의 중심과 궤도에는 다음과 같은 보기를 들 수 있다.
 질량이 거의 같은 두 천체가 같은 중심 주위를 공전한다. (이를테면 소행성 반작용계) 질량이 거의 같은 두 천체가 같은 중심 주위를 공전한다. (이를테면 소행성 반작용계)
|
 질량이 조금 다른 두 천체가 같은 중심 주위를 공전한다. (이를테면, 명왕성과 카론계) 질량이 조금 다른 두 천체가 같은 중심 주위를 공전한다. (이를테면, 명왕성과 카론계)
|
 질량이 어느 정도 다른 두 천체가 같은 중심 주위를 공전한다. (이를테면, 지구와 달의 계) 질량이 어느 정도 다른 두 천체가 같은 중심 주위를 공전한다. (이를테면, 지구와 달의 계)
|
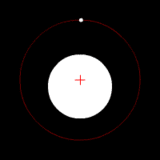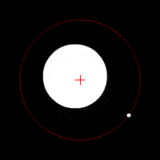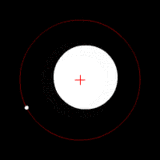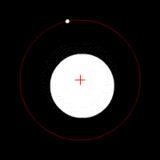 질량이 크게 다른 두 천체가 같은 중심 주위를 공전한다. (이를테면, 태양과 지구의 계) 질량이 크게 다른 두 천체가 같은 중심 주위를 공전한다. (이를테면, 태양과 지구의 계)
|
 질량이 거의 같은 두 천체가 같은 중심 주위를 타원 궤도를 그리며 공전한다. (이를테면, 쌍성 센타우루스자리 알파의 공전 형태) 질량이 거의 같은 두 천체가 같은 중심 주위를 타원 궤도를 그리며 공전한다. (이를테면, 쌍성 센타우루스자리 알파의 공전 형태)
|
외부 링크[편집]
- 중력의 중심 브리테니카 백과사전





