|
|
| 36번째 줄: |
36번째 줄: |
|
|
|
|
|
=== C<sup>1</sup>을 가정하지 않는 증명 === |
|
=== C<sup>1</sup>을 가정하지 않는 증명 === |
|
|
[[파일:Proof of Cauchy's integral theorem.svg|섬네일|삼각형 영역에 대한 코시 적분 정리의 증명 도해]] |
|
위와 같은 가정을 사용하지 않을 경우, 우선 <math>D</math>가 [[삼각형]] 영역인 경우를 보이자.<ref name="tanxj" />{{rp|85-87}} |
|
위와 같은 가정을 사용하지 않을 경우, 우선 <math>D</math>가 [[삼각형]] 영역인 경우를 보이자.<ref name="tanxj" />{{rp|85-87}} |
|
|
|
|
복소해석학에서, 코시 적분 정리(-積分定理, 영어: Cauchy's integral theorem)는 단일 연결 영역 위의 정칙 함수의 경로 적분이 경로와 무관하다는 정리이다.
정의
유계 영역  의 경계
의 경계  가 유한 개의 조각마다 매끄러운 곡선으로 이루어졌고, 양의 방향을 가지며, 연속 함수
가 유한 개의 조각마다 매끄러운 곡선으로 이루어졌고, 양의 방향을 가지며, 연속 함수  가
가  에서 정칙 함수라고 하자. 코시 적분 정리에 따르면, 다음이 성립한다.[1]:84
에서 정칙 함수라고 하자. 코시 적분 정리에 따르면, 다음이 성립한다.[1]:84

이에 따라, 단일 연결 영역  위의 정칙 함수
위의 정칙 함수  의, 임의의 두 점
의, 임의의 두 점  사이의 경로 적분
사이의 경로 적분

는 경로
![{\displaystyle \gamma \colon [a,b]\to D\qquad (\gamma (a)=z',\;\gamma (b)=z'')}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e0430dbd62f9ff26ec9af8ad7a5c8802cda12c2)
의 선택에 의존하지 않는다.
증명
C1을 가정하는 증명
도함수  가
가  의 어떤 근방
의 어떤 근방  에서 연속 함수임을 가정할 경우,[1]:84-85
에서 연속 함수임을 가정할 경우,[1]:84-85

인  을 취하자. 그렇다면, 그린 정리와 코시-리만 방정식에 의하여,
을 취하자. 그렇다면, 그린 정리와 코시-리만 방정식에 의하여,

이므로, 코시 적분 정리의 결론이 성립한다.
C1을 가정하지 않는 증명
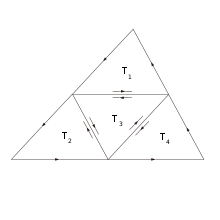 삼각형 영역에 대한 코시 적분 정리의 증명 도해
삼각형 영역에 대한 코시 적분 정리의 증명 도해
위와 같은 가정을 사용하지 않을 경우, 우선  가 삼각형 영역인 경우를 보이자.[1]:85-87
가 삼각형 영역인 경우를 보이자.[1]:85-87
귀류법을 사용하여,

이라고 가정하자.  라고 하고, 삼각형 영역
라고 하고, 삼각형 영역  의 세 변의 중점을 이어 얻는 4개의 작은 삼각형 영역
의 세 변의 중점을 이어 얻는 4개의 작은 삼각형 영역  를 생각하자. 그렇다면,
를 생각하자. 그렇다면,

이므로,

인  가 존재한다. 이와 같이 반복하면, 다음을 만족시키는 삼각형 영역의 열
가 존재한다. 이와 같이 반복하면, 다음을 만족시키는 삼각형 영역의 열  을 얻는다.
을 얻는다.



따라서,

인  가 존재하며, 임의의
가 존재하며, 임의의  에 대하여,
에 대하여,

이다.

이므로, 이는 모순이다.
이제, 일반적인 경우를 보이자.  는 유한 개의 단일 연결 영역의 합집합으로 분할되므로, 편의상
는 유한 개의 단일 연결 영역의 합집합으로 분할되므로, 편의상  가 단일 연결 영역이라고 가정하자.
가 단일 연결 영역이라고 가정하자.
임의의  에 대하여,
에 대하여,  는 균등 연속 함수이므로, 다음을 만족시키는 다각형 영역
는 균등 연속 함수이므로, 다음을 만족시키는 다각형 영역  가 존재한다.
가 존재한다.


다각형 영역  는 유한 개의 삼각형 영역의 합집합으로 분할되므로,
는 유한 개의 삼각형 영역의 합집합으로 분할되므로,

이며, 따라서

이다.
각주
외부 링크
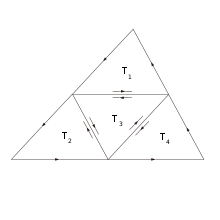









![{\displaystyle \gamma \colon [a,b]\to D\qquad (\gamma (a)=z',\;\gamma (b)=z'')}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e0430dbd62f9ff26ec9af8ad7a5c8802cda12c2)




























