그레이엄 스캔

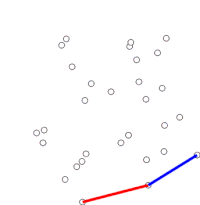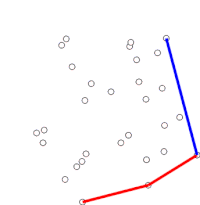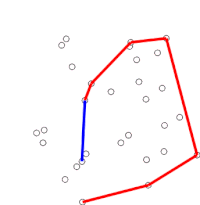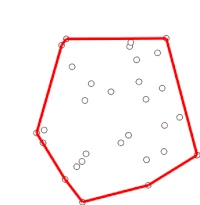
그레이엄의 스캔(Graham Scan)은 평면상에서 유한한 점들의 볼록 껍질을 찾는 방법으로, 시간 복잡도는 O(n log n)이다. 이것의 이름은 로널드 그레이엄이 1972년 원시 알고리즘을 출판한 뒤에 붙여졌다.^[1] 이 알고리즘은 볼록껍질의 모든 정점들을 테두리를 따라 찾는다. 그이 알고리즘은 경계의 오목성을 효율적으로 감지하고 제거하기 위해 스택을 사용한다.

알고리즘[편집]

첫 단계로 y좌표가 가장 작은 점을 찾는다. 만약 y좌표가 가장 작은 점이 두 개 이상일 경우, 그 중에서 x좌표가 가장 작은 점을 고른다. 이 점을 P라고 하자. 이 단계는 점의 개수를 n이라고 할 때 O(n)에 수행된다.

다음으로, 점들의 집합은 점 P로부터 x축에 대해 각도가 증가하는 순으로 정렬된다. 모든 일반적인 목적의 정렬 알고리즘은 이 과정에 적절하다. 예로, 힙 정렬 (O(n log n))이 사용될 수 있다.

각도 순으로 정렬할 때 각을 계산할 필요는 없으며, 구간 $[0,\pi ]$ 에서 단조인 임의의 함수를 사용할 수 있다. 스칼라곱을 이용하여 쉽게 계산할 수 있는 코사인이나, P에서 점까지의 직선의 기울기를 사용할 수도 있다. 만약 수의 정밀도가 중요할 때, 정렬 알고리즘에 사용하는 비교 함수는 외적의 부호를 통해 상대각(좌회전, 우회전)을 판정할 수 있다.

알고리즘은 정렬된 배열의 각 점들을 순차적으로 처리한다. 각 점마다 우선 바로 앞의 두 점을 지나서 이 점으로 도달할 때 어느 방향으로 회전하는지를 판정한다. 우회전할 경우 맨 끝에서 두 번째 점은 볼록 껍질에 속하지 않고 그 '안에' 있음을 알 수 있다. 그런 다음에는 현재의 점과 내부에 있는 것으로 판정한 점 바로 앞의 두 점에 대해 동일한 판정을 반복하며, 좌회전이 될 경우 껍질 내부에 있는 점을 제외하고(다시 고려할 필요가 없으므로) 다음 점으로 넘어간다. (어떤 경우에는 볼록 껍질의 경계 위에 있는 모든 점을 찾아야 하기 때문에, 어느 단계에서든 세 점이 한 직선 위에 있을 때는 그 점을 버리거나 이를 보고할 수 있다.)

여기서도 세 점이 좌회전 혹은 우회전을 구성하는지 판정하는 데는 두 직선이 이루는 각을 실제로 구할 필요가 없으며, 간단한 계산으로 구할 수 있다. 세 점 $P_{1}=(x_{1},y_{1})$ , $P_{2}=(x_{2},y_{2})$ , $P_{3}=(x_{3},y_{3})$ 에 대해 두 벡터 ${\overrightarrow {P_{1}P_{2}}}$ 와 ${\overrightarrow {P_{1}P_{3}}}$ 의 외적의 z좌표를 식 $(x_{2}-x_{1})(y_{3}-y_{1})-(y_{2}-y_{1})(x_{3}-x_{1})$ 으로 구할 수 있다. 이 값이 0이면 세 점이 한 직선 위에 있고, 양수이면 "좌회전", 즉 반시계 방향이며, 음수이면 "우회전", 즉 시계 방향이다.

이 과정이 처음 시작한 점으로 돌아오면 알고리즘이 종료된 것이며, 스택에는 반시계 방향 순서로 볼록 껍질 위에 있는 점이 저장되어 있다.

시간 복잡도[편집]

점들을 정렬하는 데 필요한 시간 복잡도는 O(n log n)이다. 반복문 부분의 시간 복잡도는 O(n²)처럼 보일 수 있지만, 각 점마다 뒤로 돌아가서 이전 점이 "우회전"을 하는지만 확인하며, 각 점을 최대 2번까지만 확인한다고 생각할 수 있기 때문에 실제로는 O(n)이다. 각 점은 "좌회전"의 $(x_{2},y_{2})$ 로 한 번(이후에는 다음 점 $(x_{3},y_{3})$ 으로 넘어가므로), "우회전"의 $(x_{2},y_{2})$ 로 한 번(이후에는 이 점 $(x_{2},y_{2})$ 이 제거되므로)어 등장한다. 정렬에 필요한 시간 복잡도가 실제로 볼록 껍질을 계산하는 시간보다 길기 때문에 전체 시간 복잡도는 O(n log n)이다.

의사코드[편집]

아래의 코드는 함수 ccw를 사용하며, ccw > 0이면 세 점이 반시계 방향으로, ccw < 0이면 시계 방향으로 꺾이며, ccw = 0이면 한 직선 위에 있다. (실제 응용에서는 좌표가 임의의 실수일 경우 이 함수가 부동소수점 비교를 정확히 수행해야 하며, "거의" 한 직선 위에 있는 점에서 발생하는 수치적 특이점에도 유의해야 한다.)

계산 결과를 stack에 저장하는 것으로 하자.

let points be the list of points
let stack = empty_stack()

find the lowest y-coordinate and leftmost point, called P0
sort points by polar angle with P0, if several points have the same polar angle then only keep the farthest

for point in points:
    # pop the last point from the stack if we turn clockwise to reach this point
    while count stack > 1 and ccw(next_to_top(stack), top(stack), point) <= 0:
        pop stack
    push point to stack
end

이제 스택에는 P0이 첫 점이고 반시계 방향으로 정렬되어 있는 볼록 껍질이 들어 있다.

여기서 next_to_top()은 스택을 변경하지 않고 꼭대기에서 바로 아래에 있는 원소를, top()은 꼭대기에 있는 원소를 반환하는 함수이다.

이 의사코드는 Introduction to Algorithms에서 가져온 것이다.

참고[편집]

이 알고리즘의 기본 개념은 입력이 각도 대신 x좌표로 정렬되어 있어도 적용할 수 있으며, 이때는 볼록 껍질의 위쪽과 아래쪽을 두 단계에 걸쳐 계산한다. 이렇게 수정된 알고리즘은 A. M. Andrew^[2]가 고안했으며 Andrew's Monotone Chain Algorithm으로 알려져 있다. 이 알고리즘은 그레이엄 스캔과 기본 성질이 같다.^[3]

그레이엄 스캔에서 스택을 활용하는 기법은 모든 최근접 최솟값 문제와 매우 비슷하며, 이 문제를 해결하는 병렬 알고리즘을 (그레이엄 스캔처럼) 정렬된 점들의 볼록 껍질을 효율적으로 계산하는 데도 사용할 수 있다.^[4]

수치적 정밀성[편집]

유한 정밀도 부동소수점 산술을 사용하는 알고리즘에서는 수치적 정밀성이 문제가 된다. 2004년의 논문에서는 특히 그레이엄 스캔을 구현하는 데 사용할 수 있는 간단한 증분 전략을 분석하였다.^[5] 이 논문에서 제시한 목표는 특히 이 알고리즘을 분석하는 것이라기보다는 계산기하학에서 어떤 부동소숫점 계산이 어떻게 실패할 수 있을지에 대한 교과서적 예제를 제공하는 것이었다.^[5] 나중에 D. Jiang과 N. F. Stewart가 이 논문에 부연하여 역방향 오차 분석을 통해 두 가지 중요한 결론을 이끌어냈다. 하나는 볼록 껍질이 well-conditioned인 문제이므로 이 문제를 해결하는 알고리즘의 오차가 합리적인 범위 이내일 것을 기대할 수 있다는 것이며, 다른 하나는 저자들이 (Steven Fortune의 이름을 따) Graham-Fortune이라고 부르는 그레이엄 스캔의 변형 알고리즘이 유한 정밀도와 정확하지 않은 값 문제를 "해결할 수 있는 최대한의 한도 내에서" 해결할 수 있음을 보인 것이다.

같이 보기[편집]

볼록 껍질 알고리즘

각주[편집]

↑ Graham, R.L. (1972). “An Efficient Algorithm for Determining the Convex Hull of a Finite Planar Set” (PDF). 《Information Processing Letters》 1 (4): 132–133. doi:10.1016/0020-0190(72)90045-2.
↑ Andrew, A. M. (1979). “Another efficient algorithm for convex hulls in two dimensions”. 《Information Processing Letters》 9 (5): 216–219. doi:10.1016/0020-0190(79)90072-3.
↑ De Berg, Mark; Cheong, Otfried; Van Kreveld, Marc; Overmars, Mark (2008). 《Computational Geometry Algorithms and Applications》. Berlin: Springer. 2–14쪽. doi:10.1007/978-3-540-77974-2. ISBN 978-3-540-77973-5.
↑ Berkman, Omer; Schieber, Baruch; Vishkin, Uzi (1993). “Optimal double logarithmic parallel algorithms based on finding all nearest smaller values”. 《Journal of Algorithms》 14 (3): 344–370. CiteSeerX 10.1.1.55.5669. doi:10.1006/jagm.1993.1018. .
↑ ^가 ^나 Kettner, Lutz; Mehlhorn, Kurt; Pion, Sylvain; Schirra, Stefan; Yap, Chee (2008). “Classroom examples of robustness problems in geometric computations” (PDF). 《Computational Geometry》 40 (1): 61–78. doi:10.1016/j.comgeo.2007.06.003. (An earlier version was reported in 2004 at ESA'2004)

[1] Graham, R.L. (1972). “An Efficient Algorithm for Determining the Convex Hull of a Finite Planar Set” (PDF). 《Information Processing Letters》 1 (4): 132–133. doi:10.1016/0020-0190(72)90045-2.

[2] Andrew, A. M. (1979). “Another efficient algorithm for convex hulls in two dimensions”. 《Information Processing Letters》 9 (5): 216–219. doi:10.1016/0020-0190(79)90072-3.

[3] De Berg, Mark; Cheong, Otfried; Van Kreveld, Marc; Overmars, Mark (2008). 《Computational Geometry Algorithms and Applications》. Berlin: Springer. 2–14쪽. doi:10.1007/978-3-540-77974-2. ISBN 978-3-540-77973-5.

[4] Berkman, Omer; Schieber, Baruch; Vishkin, Uzi (1993). “Optimal double logarithmic parallel algorithms based on finding all nearest smaller values”. 《Journal of Algorithms》 14 (3): 344–370. CiteSeerX 10.1.1.55.5669. doi:10.1006/jagm.1993.1018. .

[mkpsy-5] 가 ^나 Kettner, Lutz; Mehlhorn, Kurt; Pion, Sylvain; Schirra, Stefan; Yap, Chee (2008). “Classroom examples of robustness problems in geometric computations” (PDF). 《Computational Geometry》 40 (1): 61–78. doi:10.1016/j.comgeo.2007.06.003. (An earlier version was reported in 2004 at ESA'2004)

[1]

[2]

[3]

[4]

[5]