국소성의 원리

국소성의 원리(principle of locality)란 공간적으로 멀리 떨어져있는 두 물체는 절대 서로 직접적으로 영향을 줄 수 없다는 물리학 원리이다. 한 물체가 다른 물체에게 영향을 미치기 위해서는 반드시 둘 사이의 공간이 매개되어야 한다. 이것은 아인슈타인의 "양자역학과 실재"라는 글에서 처음으로 다음과 같이 명시되었다.

앞으로 이야기할 논의는 공간상으로 떨어져있는 두 물체 A와 B의 상대적 독립성에 대한 것이다. A에게 어떤 외부의 영향이 주어진다고 해도 그것은 B에게 직접 영향을 주지 않는다. 이것은 국소작용의 원리로 알려져 있고, 아직까지는 장 이론에서만 의미있게 사용되고 있다. 만약 이 주장이 완전히 틀린 것이라면, 닫힌 계는 존재할 수 없을 것이고 따라서 물리 법칙들의 공리들 역시 실험적으로 타당하게 증명할 수 없을 것이다.

예

지구의 공전 모형을 생각해 보자. 이 우주에 지구와 태양만 존재하고, 지구는 태양의 주위를 공전하고 있다고 가정한다. 뉴턴 역학에 따르면, 태양이 어느 순간 이 우주에서 사라져버린다면, 지구가 궤도에서 벗어나는 순간 직선 운동을 하게 된다.

하지만 이는 국소성의 원리에 위배된다. 국소성의 원리에 따르면 태양이 사라진 직후에, 그 영향은 태양 주변부에만 미치게 되고 이것이 점차적으로 전파되어 지구에 영향을 주게 된다. 이때 그 영향이 전파되는 속도는 빛의 속도와 같고, 이는 일반상대성이론의 결론 중 하나이다. 국소성의 원리가 정확히 적용되고 있음을 볼 수 있다.

양자 역학 이전

17세기에 뉴턴의 만유인력 원리는 "원거리 작용"이라는 용어로 정식화되어 국소성 원리를 위반했다. 뉴턴 자신도 이 위반이 터무니없다고 생각했다.

무생물이 물질이 아닌 다른 것의 매개 없이 상호 접촉 없이 다른 물질을 작용하고 영향을 미친다는 것은 상상할 수 없다…중력은 물질에 타고나야 하고, 내재되어 있어야 하며, 그래서 한 물체가 진공을 통해 멀리 떨어진 곳에서 다른 물체에 작용하고, 그 작용과 힘이 서로 전달될 수 있는 다른 것의 매개 없이, 나는 그 어떤 것의 매개도 없이, 내가 철학적 문제에 유능한 사고력을 가진 사람은 결코 그것에 빠질 수 없다고 믿을 정도로 큰 부조리다. 중력은 대리인이 특정 법칙에 따라 끊임없이 행동함으로써 발생해야 하지만, 이 대리인이 물질이든 비물질이든, 나는 독자들의 배려에 맡겼다.

— Isaac Newton, Letters to Bentley, 1692/3

쿨롱의 전기력 법칙은 처음에는 원거리에서의 순간 작용으로 공식화되었지만 1880년 제임스 클러크 맥스웰은 국소성을 따르는 장 방정식이 전자기학의 모든 현상을 예측한다는 것을 보여주었다. 이 방정식은 전자기력이 빛의 속도로 전파된다는 것을 보여준다.

1905년 알베르트 아인슈타인의 특수 상대성 이론은 어떤 물질이나 에너지도 빛의 속도보다 빠르게 이동할 수 없다고 가정했고, 이에 따라 아인슈타인은 국소성의 원리를 따르는 방식으로 물리학을 재구성하려고 했다. 그는 나중에 국소성 원리를 따르는 대안적인 중력 이론인 일반 상대성 이론을 만드는 데 성공했다.

그러나 아인슈타인 자신이 발전에 도움을 준 양자 역학에서 국소성의 원리에 대한 다른 도전이 이후에 발전했다.

국소성을 위한 모델

양자역학의 국소성에 대한 다이어그램

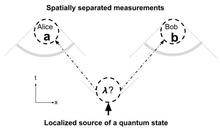
간단한 시공간 다이어그램은 국소성과 관련된 문제를 명확하게 하는 데 도움이 될 수 있다. 양자 역학 논의에 적합한 국소성 문제를 설명하는 방법이 다이어그램에 설명되어 있다. 입자는 한 위치에서 생성된 다음 공간적으로 분리된 다른 두 위치에서 분할되어 측정된다. 두 측정값은 엘리스와 밥의 이름을 따서 명명되었다. 엘리스는 측정 (A)을 수행하고 결과 $\mathbf {a}$를 얻는다. 밥은 측정 ($B$)을 수행하고 결과 $\mathbf {b}$를 얻는다. 실험을 여러 번 반복하고 결과를 비교한다.

시공간 속의 앨리스와 밥

시공간 다이어그램의 앨리스와 밥

시공간 다이어그램에는 수직 방향의 시간 좌표와 수평 방향의 공간 좌표가 있다. 왼쪽 국소에 있는 앨리스는 그림과 같이 미래에 확장되는 원뿔에서만 사건에 영향을 미칠 수 있다. 유한한 빛의 속도로 인해 그녀는 이 경우 밥의 위치를 포함한 다른 영역에 영향을 미치지 않는다. 마찬가지로 우리는 다이어그램을 사용하여 밥의 국소적 상황이 동시에 엘리스에 의해 변경될 수 없다고 추론할 수 있다. 밥에게 영향을 미치는 모든 사건은 다이어그램에서 밥의 위치 아래 원뿔에 있다. 엘리스 주변의 점선은 그녀의 유효한 미래 위치를 보여준다. 밥 주위의 점선은 그의 현재 상황을 야기할 수 있는 사건을 보여준다. 앨리스가 자신이 있는 위치에서 양자 상태를 측정하면 결과에 라벨 $\mathbf {a}$이 붙는다.; 마찬가지로 밥은 $\mathbf {b}$. 국소성 모델은 이러한 측정값 사이의 통계적 관계를 설명하려고 시도한다.

원거리에서의 작용

원거리에서의 행동

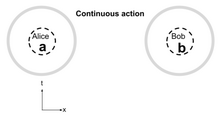
가장 단순한 국소성 모델은 국소성이 없다는 것이다. 즉, 상대성 이론에 대한 제한이 없는 거리에서 순간적인 작용이 발생하는 것이다. 원거리 작용에 대한 국소성 모델을 연속 작용이라고 하다. 회색 영역(여기서 원)은 "화면"이라 부르는 수학적 개념이다. 한 위치에서 화면을 통과하는 모든 경로는 해당 위치의 물리적 모델의 일부가 된다. 회색 고리는 공간과 시간의 모든 부분에서 발생하는 사건이 엘리스 또는 밥이 측정한 확률에 영향을 미칠 수 있음을 나타낸다. 따라서 연속 작용의 경우 모든 시간과 장소의 사건이 엘리스와 밥의 모델에 영향을 미친다. 이 간단한 모델은 뉴턴 중력을 사용하는 태양 행성 역학과 상대론적 효과가 중요하지 않은 정전기학에서 아주 성공적이다.

미래 입력 의존성 없음

미래 입력 의존성 없음

많은 국소성 모델은 미래 사건의 가능한 영향을 명시적으로 또는 암시적으로 무시한다. 오른쪽의 시공간 다이어그램은 연속 작용과 결합될 때 이러한 제한의 효과를 보여준다. 미래의 입력(점선 위)은 더 이상 엘리스 또는 밥 모델의 일부로 여겨지지 않는다. 이 다이어그램을 연속 작용에 대한 다이어그램과 비교하면 이들이 동일한 국소성 모델이 아니라는 것이 분명해진다. 현재에 영향을 미치지 않는 미래에 대한 상식적인 주장은 합리적인 기준이지만 그러한 가정은 모델의 수학적 특성을 바꾸어야 성립한다.

벨의 국소적 인과성

벨의 국소적 인과성

존 스튜어트 벨은 벨의 정리를 논의할 때 오른쪽에 표시된 선별 모델을 사용한다. 엘리스와 밥의 공통 과거에 있었던 사건은 화면이 해당 사건을 흡수하는 방식으로 표시된 대로 엘리스와 밥에 대한 확률을 계산하는 데 사용되는 모델의 일부이다. 단, 엘리스 측정 중 밥의 위치에서 발생하는 사건와 향후 사건는 제외된다. 벨은 이 가정을 국소적 인과성이라고 불렀지만, 다이어그램을 사용하면 국소적 인과관계의 다른 의미와 결합된 다른 국소적 의미에 의해 넘어지지 않고 가정의 의미에 대해 추론할 수 있다. 점선은 엘리스 또는 밥의 과거 상대론적으로 유효한 영역을 보여준다. 회색 호는 가정된 벨 "화면"이다.

양자 역학

예를 들어 쉽게 구별할 수 있는 소수의 행성의 상대적 위치는 직접 볼 수 있다. 상대적 위치를 이해하고 측정하는 것은 기술적인 문제만 제기하다. 반면에 초미세 세계는 무작위로 보이는 많은('통계적' 또는 '확률적') 사건에 대한 평균을 구하는 측정을 통해서만 알려져 있으며, 측정은 설계에 따라 입자와 같은 결과나 파동과 같은 결과를 보여줄 수 있다. 이 세계는 양자역학에 의해 지배된다. 국소성의 개념은 더욱 복잡하며 확률과 상관관계의 언어로 설명된다.

1935년 EPR 논문 에서 Albert Einstein, Boris Podolsky 및 Nathan Rosen은 그러한 실험을 상상했다. 그들은 양자 역학이 현재 양자 얽힘으로 알려진 것을 예측한다는 것을 관찰하고 그 결과를 조사했다. 그들의 관점에서, 국소성의 고전적 원리는 어떤 측정의 결과로 밥의 위치에서 "실질적인 변화가 일어날 수 없다"는 것을 암시했다. 하고 있었다. 양자 역학은 밥의 측정 선택에 따라 파동함수 붕괴를 예측하기 때문에 이것이 원거리 작용의 한 형태이며 파동함수는 현실을 완전히 설명할 수 없다고 결론지었다. 물리학자들은 동의하지 않았다. 그들은 양자 파동함수를 완전한 것으로 받아들이고 EPR 논문에서 가정된 국소성과 현실의 본질에 의문을 제기했다.

1964년에 존 스튜어트 벨은 양자 이론에 의해 예측된 공간적으로 분리된 입자 사이의 상관 관계를 설명하기 위해 국소 숨겨진 변수를 사용하여 양자 이론을 "완성"하려는 아인슈타인의 목표를 달성하는 것이 가능한지 여부를 조사했다. 벨은 얽힌 입자들 사이의 상관관계의 구체적인 값을 측정함으로써 국소 숨은 변수 이론과 양자 이론을 구별하는 기준을 확립했다. 후속 실험에서 일부 양자 효과가 벨의 부등식을 위반하며 국소 숨은 변수 이론으로 재현할 수 없음을 보여주었다. 벨의 정리는 신중하게 정의된 국소성 모델에 따라 달라진다.

국소성과 숨겨진 변수

벨은 양자역학의 분석에 필요한 확률이라는 측면에서 국소적 인과관계를 설명했다. $P(\mathbf {r} |g)$과 같은 표기법을 사용하여 주어진 상태 $g$에 대해 결과가 $\mathbf {r}$일 확률을 나타낸다. 벨은 다음 확률 분포를 조사했다.$$P(\mathbf {ab} |AB,\lambda )$$여기서 $\lambda$는 두 입자가 처음에 같은 위치에 있을 때 숨겨진 상태 변수 세트(국소적으로)를 나타낸다. 국소 인과관계가 성립한다면 엘리스와 밥이 관찰한 확률은 숨겨진 변수에 의해서만 결합되어야 하며 우리는 다음을 보여줄 수 있다.$$P(\mathbf {ab} |AB,\lambda )=P(\mathbf {a} |A,\lambda )P(\mathbf {b} |B,\lambda ),$$벨은 이 인수분해의 결과가 벨 부등식으로 알려진 엘리스와 밥이 관찰한 상관 관계에 대한 한계임을 증명했다. 양자 역학은 이 한계보다 더 강한 상관 관계를 예측하기 때문에 EPR 논문에서 원하는 대로 국소적로 설정된 숨겨진 변수를 "완전한" 양자 이론에 추가할 수 없다.

국소성 문제를 조사하기 위해 특별히 고안된 수많은 실험은 양자 역학의 예측을 확인한다. 여기에는 두 측정 위치가 1km 이상 떨어져 있는 실험이 포함된다. 2022년 노벨 물리학상은 부분적으로 "벨 부등식의 위반을 입증한 얽힌 광자 실험"으로 알랭 아스펙트, 존 클라우저 및 안톤 차일링거에게 수여되었다. 이러한 상관 관계를 이끌어내는 양자 이론의 특정 측면을 양자 얽힘이라고 하며 벨의 시나리오 버전은 이제 얽힘을 실험적으로 확인하는 데 사용된다.

용어

벨의 수학적 결과는 실험 데이터와 비교할 때 국소적 숨겨진 변수 수학적 양자 이론을 제거하다. 그러나 물리적 세계에 관한 수학의 해석은 여전히 논쟁의 여지가 있다. 벨은 자신의 작업 뒤에 있는 가정을 "국소적 인과성", 줄여서 "국소성"으로 설명했다. 나중에 저자들은 가정을 국소적 현실주의라고 불렀다. 이러한 다른 이름은 수학적 가정을 변경하지 않는다.

이 문구를 사용한 논문을 검토하면 실재론에 대한 일반적인 (고전적인) 물리학 정의는 다음과 같다.

측정 결과가 측정 전에 잘 정의되어 있고 측정과 독립적이라는 가정.

이 정의에는 양자 중첩과 충돌하는 "잘 정의된" 및 속성의 (형이상학적) 사전 존재를 암시하는 "...측정 이전"과 같은 고전적 개념이 포함된다. 특히, 벨 정리의 맥락에서 국소적 실재론이라는 용어는 벨 스크리닝 가정이 암시하는 종류가 아닌 국소성을 포함하는 일종의 "실재론"으로 볼 수 없다. 실재론의 공통 개념과 양자역학 사이의 이러한 갈등은 국소적 실재론이 논의될 때마다 주의 깊은 분석을 요구한다. ^:98공간적으로 잘 분리된 두 측정의 결과가 서로 인과적으로 영향을 미칠 수 없다는 "국소성" 수정자를 추가하면 이 조합이 벨의 증명과 관련이 없게 된다. 벨이 취한 유일한 해석은 그가 국소적 인과관계라고 부르는 해석이었다. ^:98결과적으로 벨의 정리는 소급인과율이나 초결정론 에 기초한 이론뿐만 아니라 비국소적 변수의 가능성을 제한하지 않는다.

파동 함수 붕괴의 확률적 특성으로 인해 양자역학의 이러한 명백한 국소성 위반은 통신 불가 정리에 따라 빛보다 빠르게 정보를 전송하는 데 사용될 수 없다. 애셔 페레스는 약한 비국소성과 강한 비국소성을 구별하며, 후자는 빛보다 빠른 의사소통을 가능하게 하는 이론을 뜻한다. 이러한 용어에 따라 양자 역학은 약한 비국소적 상관관계를 허용하지만 강한 비국소성은 허용하지 않는다.

상대론적 양자역학

양자장론의 주요 원리 중 하나는 국소성의 원리이다. 장의 역학을 설명하는 장 연산자와 라그랑지언 밀도는 상호 작용이 원격 작용으로 설명되지 않는다는 의미에서 국소적이다. 이는 먼 좌표에 의존하는 두 장의 곱인 라그랑지안의 항을 피함으로써 달성할 수 있다. 구체적으로, 상대론적 양자장론에서 국소성과 인과성의 원칙을 강화하려면 다음 조건이 필요하다. 두 개의 관측 가능량이 있고, 각각은 서로 공간적으로 분리되어 있는 두 개의 별개의 시공간 영역 내에 국한되어 있으며, 관측 가능량들은 반드시 가환이어야 한다. 이 조건은 때때로 상대론적 양자장론의 공리 중 하나로 부과된다.

EPR 역설

아인슈타인은 양자역학의 체계가 국소성의 원리에 모순된다고 지적했으나, 숨은 변수 찾기와 관련된 여러 실험을 통해 오히려 양자 세계에서 국소성의 원리가 통하지 않으며, 비국소적이란 것이 밝혀졌다.

같이 보기

• 국소적 숨은 변수 이론
• 송이 분해 성질